【受験算数】平面図形：黒い角度の和を求めよう【予習シリーズ算数・小5下】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 角度と面積 > 【受験算数】平面図形：黒い角度の和を求めよう【予習シリーズ算数・小5下】

【受験算数】平面図形：黒い角度の和を求めよう【予習シリーズ算数・小5下】

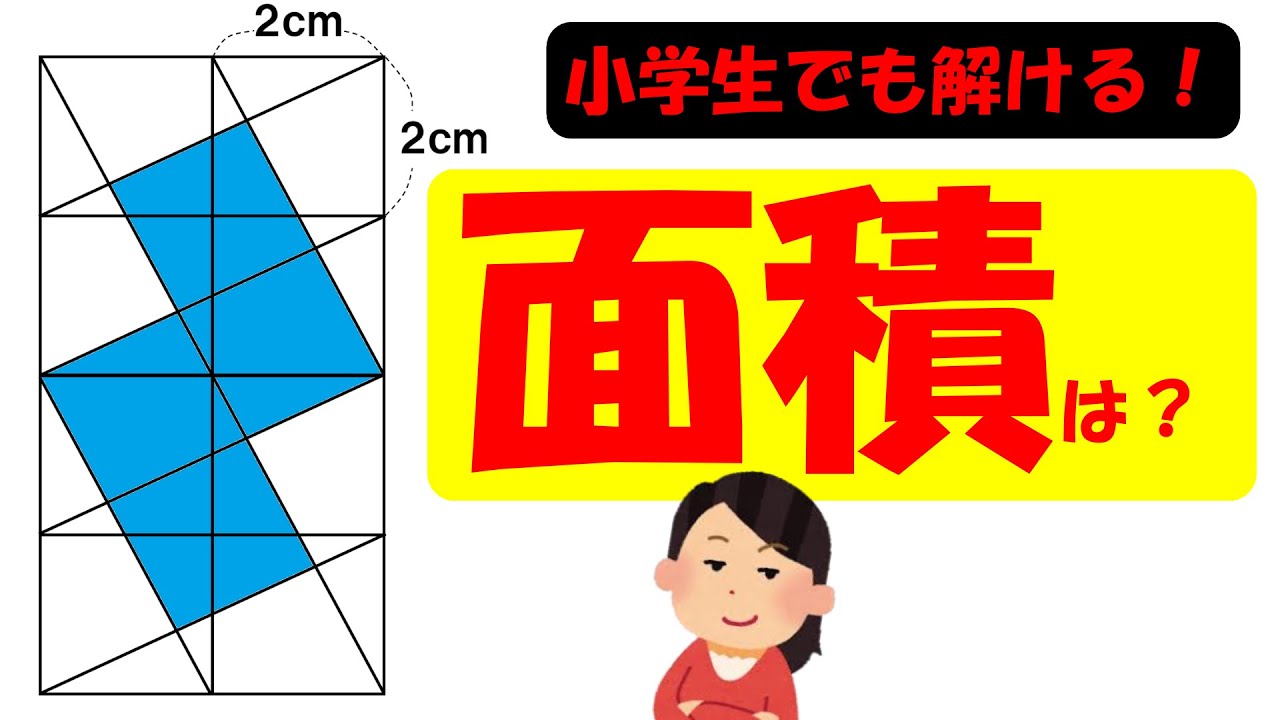
問題文全文(内容文)：
黒い角度の和はいくつでしょう。
チャプター：

00:00 問題文＋ポイント
00:12 本編　　
02:30 エンディング

単元： #算数(中学受験)#平面図形#角度と面積
教材： #予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師： 理数個別チャンネル
問題文全文(内容文)：
黒い角度の和はいくつでしょう。
投稿日：2022.08.20

＜関連動画＞

【受験算数】平面図形と比(3)：（練習❹）高さを変えて相似な図形を探せ【予習シリーズ演習問題集・小5下】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#相似と相似を利用した問題
教材： #予習シ#予習シ演問・小5下#中学受験教材#平面図形と比(3)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
高さ4.8mの街灯から4m離れたところにAさんが立っています。また、Aさんの影の 先端の地点には3mの木が立っていて、木の影がへいに1.5mうつりました。次の問 に答えよ。 (1)Aさんの身長は何cmですか。 (2)街灯からへいまでは何mありますか。
この動画を見る　

【算数】小4-37 計算のくふう①

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
算数　計算のくふう①
以下の問に答えよ
① $(14+9)\times5=$
② $(28-14)\div7=$
③ $8\times(40+3)|$
④ $200\div(20+5)=$
⑤ $109\times5=$
⑥ $7\times102=$
⑦ $96\div6=$
※図は動画内参照
この動画を見る　

３つの円は〇〇〇　　　　名古屋高校

アイキャッチ画像
単元： #数学(中学生)#中３数学#円#平面図形#角度と面積#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
面積比1：4：9の3つの円
AB=?
＊図は動画内参照

名古屋高等学校
この動画を見る　

割合の簡単な考え方#shorts

アイキャッチ画像
単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第15回割合②をショートで解説します。

この動画を見る　

三つ子素数

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#数の性質その他
指導講師： 数学を数楽に
問題文全文(内容文)：
P,P+2,P+4が全て素数のとき、3つ子素数という。
3つ子素数をすべて求めよ。
この動画を見る　
PAGE TOP