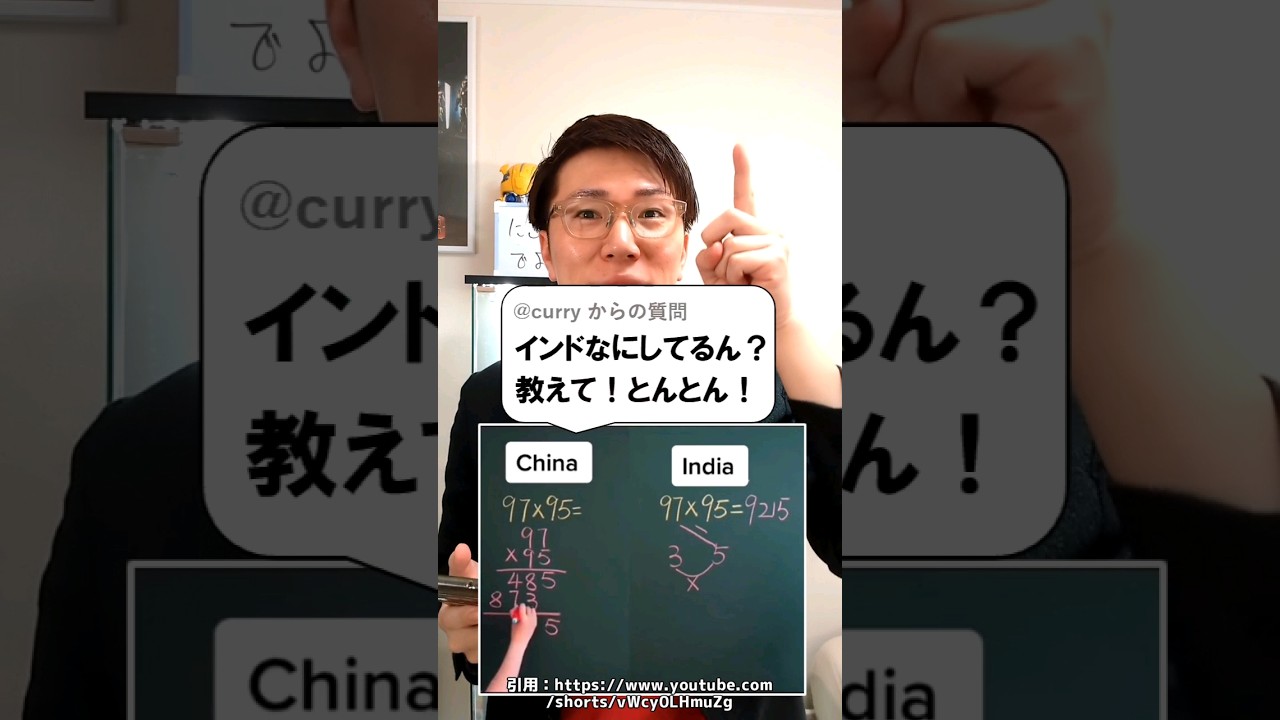
問題文全文(内容文):
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
チャプター:
0:00 オープニング
0:05 問題文
0:35 (1)解説
2:18 (2)解説
3:37 エンディング
単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
投稿日:2024.12.29