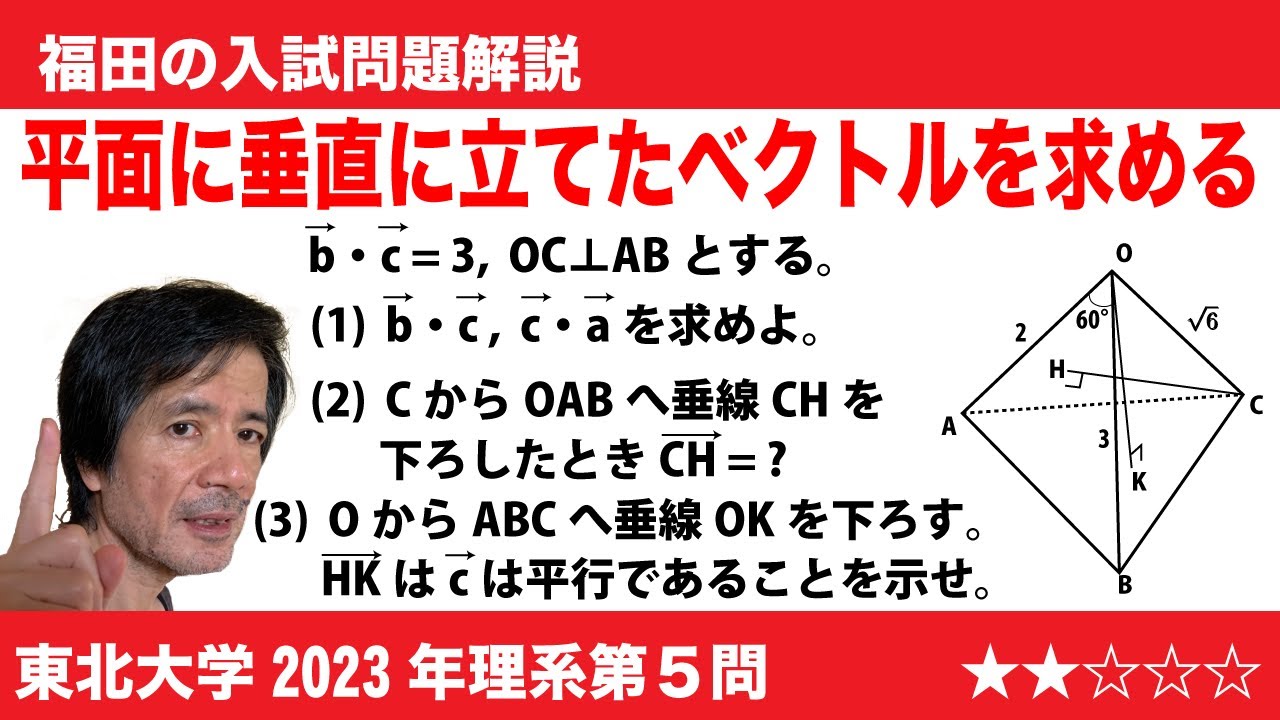
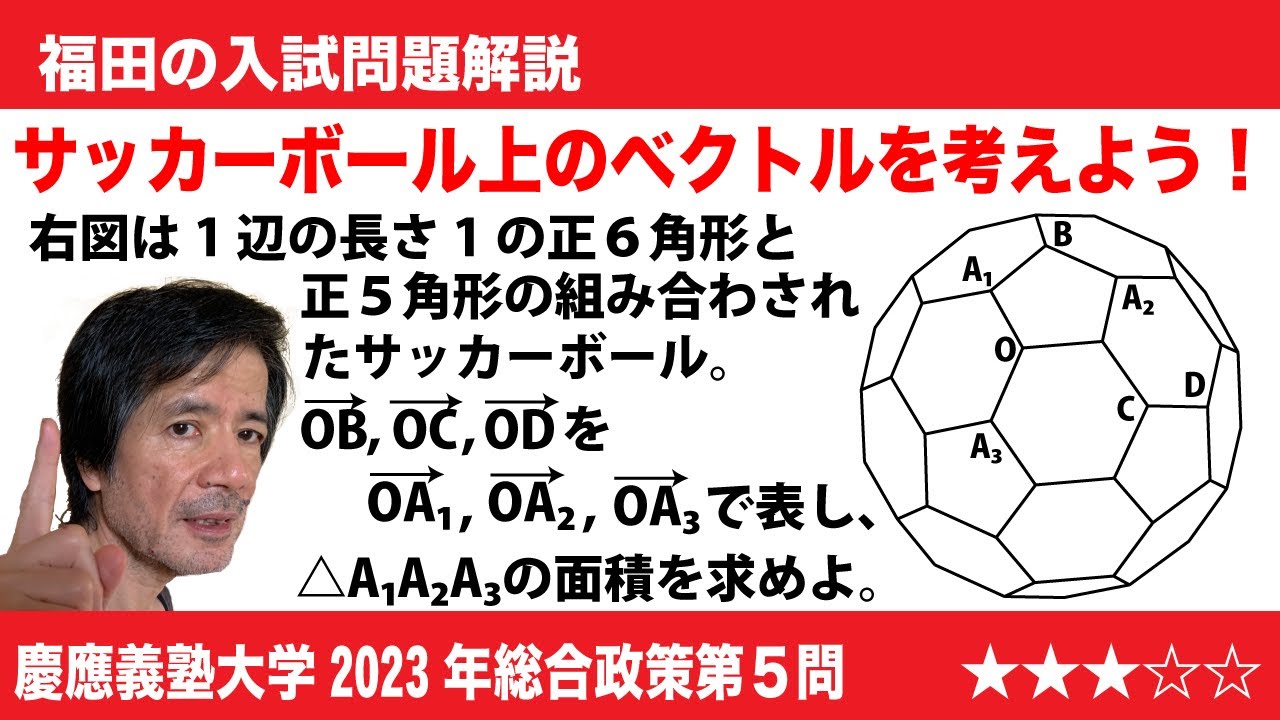
問題文全文(内容文):
$\ell:x+1=\dfrac{y-1}{a}=z$,
$\ell_2;-x+1=y+b=\dfrac{z-1}{2}$
は交わり,なす角は$60°$であるとする.
このとき,$a,b$の値を求めよ.
$\ell:x+1=\dfrac{y-1}{a}=z$,
$\ell_2;-x+1=y+b=\dfrac{z-1}{2}$
は交わり,なす角は$60°$であるとする.
このとき,$a,b$の値を求めよ.
単元:
#空間ベクトル#空間ベクトル#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\ell:x+1=\dfrac{y-1}{a}=z$,
$\ell_2;-x+1=y+b=\dfrac{z-1}{2}$
は交わり,なす角は$60°$であるとする.
このとき,$a,b$の値を求めよ.
$\ell:x+1=\dfrac{y-1}{a}=z$,
$\ell_2;-x+1=y+b=\dfrac{z-1}{2}$
は交わり,なす角は$60°$であるとする.
このとき,$a,b$の値を求めよ.
投稿日:2021.03.28