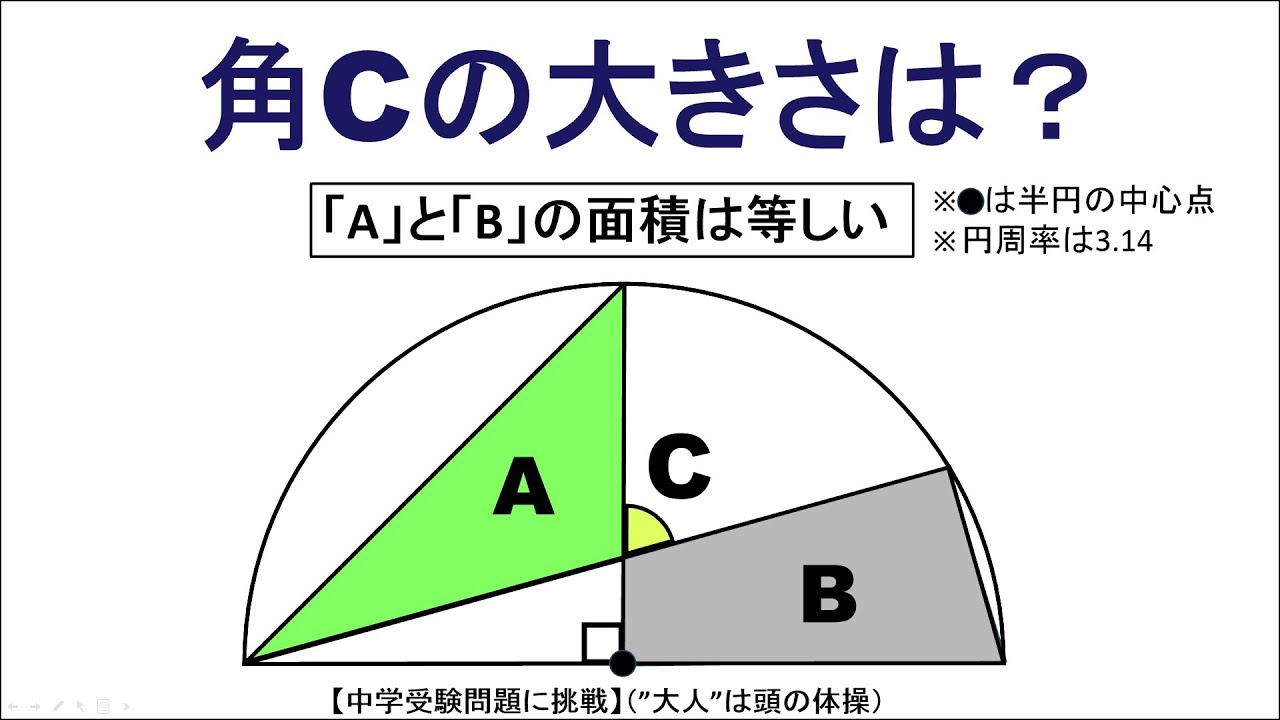
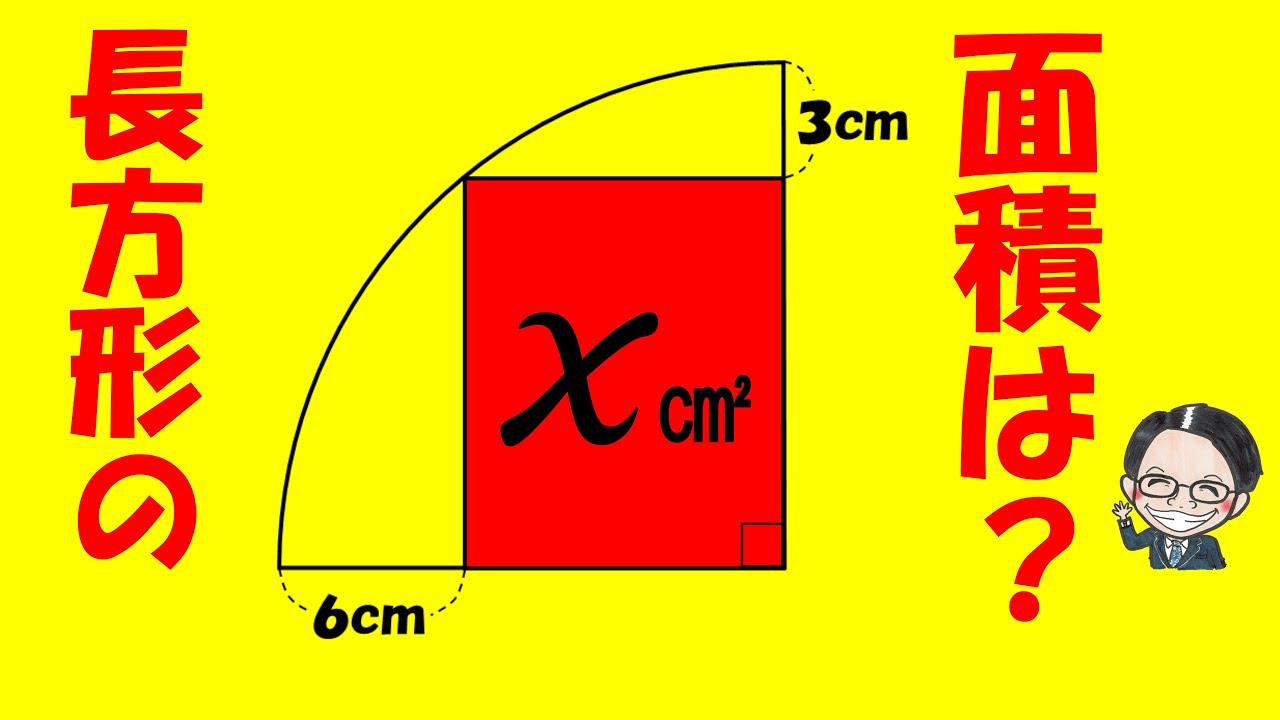
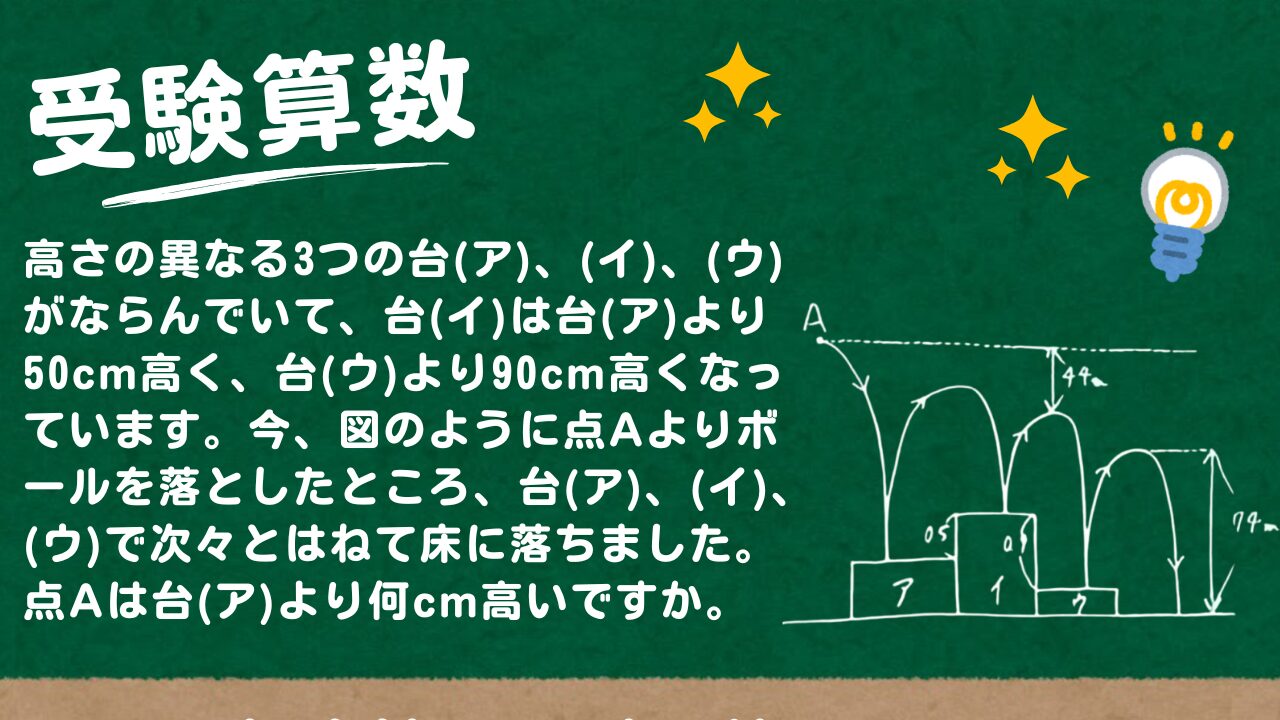
問題文全文(内容文):
(1)次の計算をし、約分でき分数で答えなさい。
5/2x3+11/3x4+19/4x5+29/5x6
(2)次郎くんはある本を読み始めて最初の五日間は同じページ数を読み進め、その後の3日間は旅行中のため一日当たり6ページ減らして読み進めました。旅行から帰ってきた後は毎日、旅行中の一日当たりの4倍のページ数を読んだところ、旅行から帰って4日目には初めて200ページを超えて、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3)下の図のような東西に4本、南北に6本のみちがあります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向、西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、遠回りすることはできます。
(1)次の計算をし、約分でき分数で答えなさい。
5/2x3+11/3x4+19/4x5+29/5x6
(2)次郎くんはある本を読み始めて最初の五日間は同じページ数を読み進め、その後の3日間は旅行中のため一日当たり6ページ減らして読み進めました。旅行から帰ってきた後は毎日、旅行中の一日当たりの4倍のページ数を読んだところ、旅行から帰って4日目には初めて200ページを超えて、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3)下の図のような東西に4本、南北に6本のみちがあります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向、西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、遠回りすることはできます。
単元:
#算数(中学受験)#計算と数の性質#中学入試
指導講師:
重吉
問題文全文(内容文):
(1)次の計算をし、約分でき分数で答えなさい。
5/2x3+11/3x4+19/4x5+29/5x6
(2)次郎くんはある本を読み始めて最初の五日間は同じページ数を読み進め、その後の3日間は旅行中のため一日当たり6ページ減らして読み進めました。旅行から帰ってきた後は毎日、旅行中の一日当たりの4倍のページ数を読んだところ、旅行から帰って4日目には初めて200ページを超えて、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3)下の図のような東西に4本、南北に6本のみちがあります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向、西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、遠回りすることはできます。
(1)次の計算をし、約分でき分数で答えなさい。
5/2x3+11/3x4+19/4x5+29/5x6
(2)次郎くんはある本を読み始めて最初の五日間は同じページ数を読み進め、その後の3日間は旅行中のため一日当たり6ページ減らして読み進めました。旅行から帰ってきた後は毎日、旅行中の一日当たりの4倍のページ数を読んだところ、旅行から帰って4日目には初めて200ページを超えて、この日にちょうどこの本を読み終えました。この本は全部で何ページありますか。
(3)下の図のような東西に4本、南北に6本のみちがあります。南スタート地点から東ゴール、西ゴール、北ゴール地点のいずれかに進む方法は全部で何通りありますか。ただし、南方向には進むことができませんが、北方向、東方向、西方向のいずれかに進むことができます。また、一度通った道を通ることはできませんが、遠回りすることはできます。
投稿日:2025.06.17