問題文全文(内容文):
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
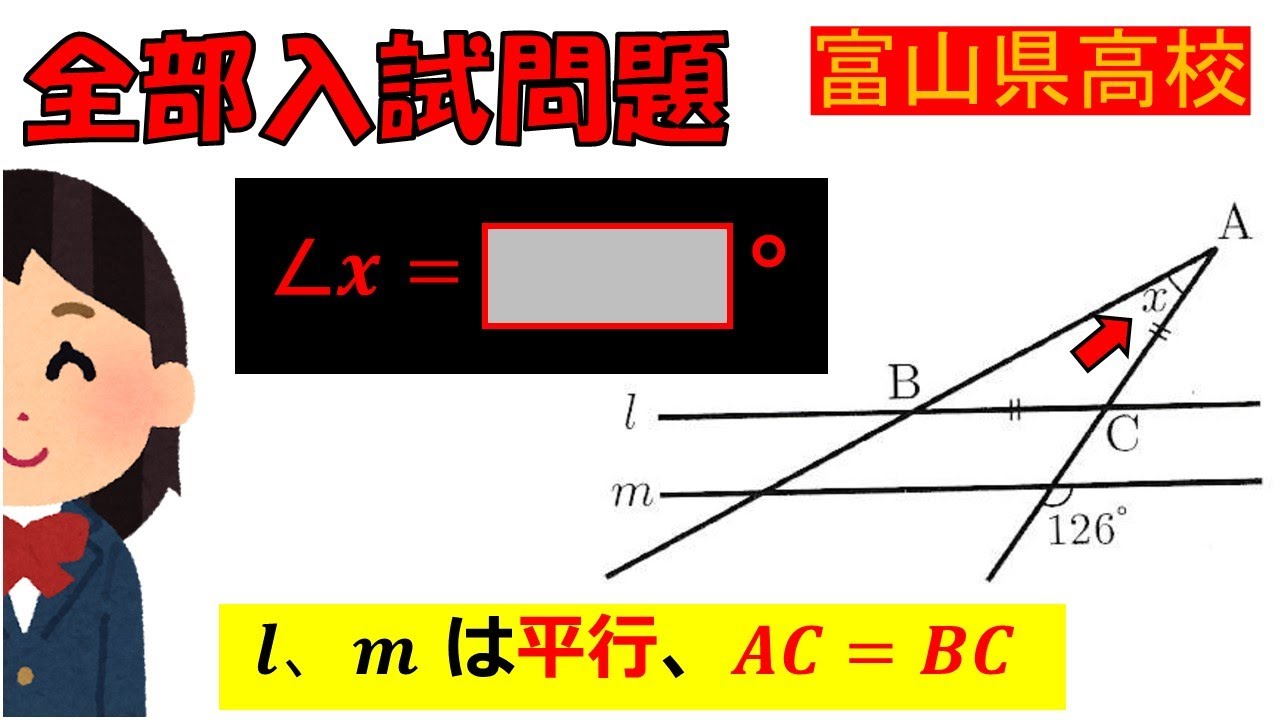
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
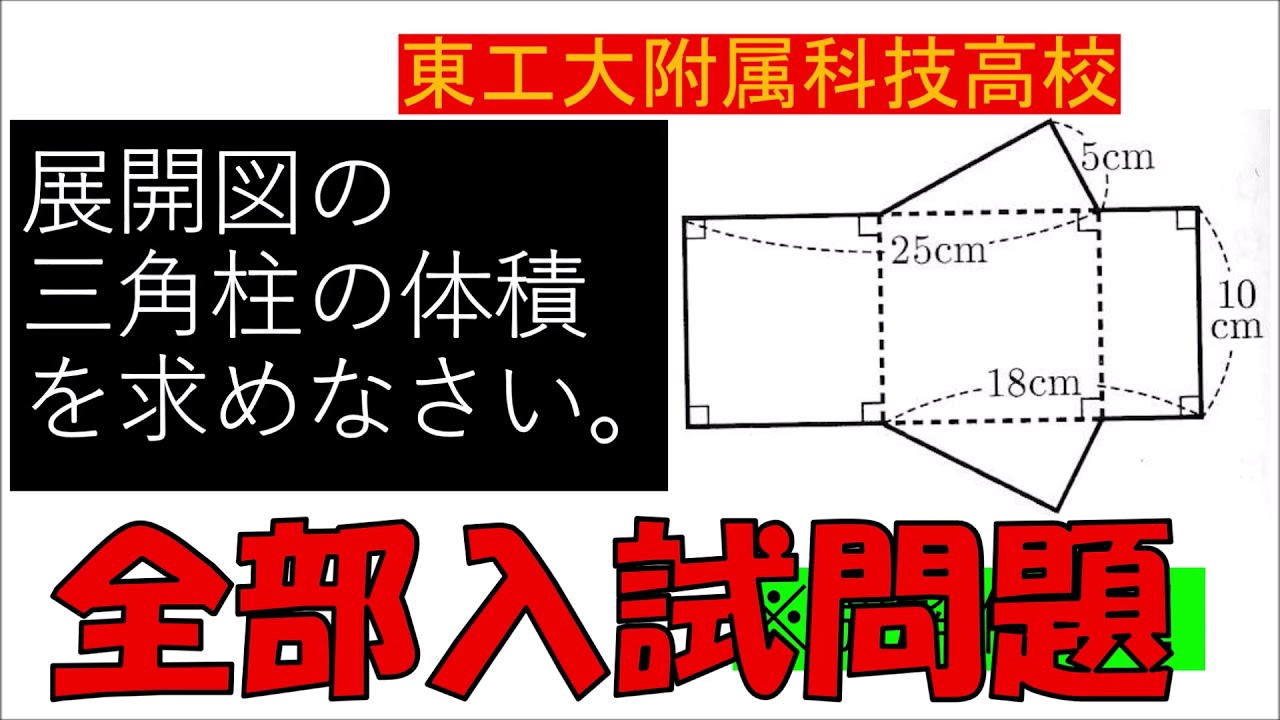
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#2次方程式#確率#立体図形#立体切断#立体図形その他#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
①$-5-(-9)$を計算せよ.
②$- 2 ^ 2 \times 3$を計算せよ.
③$xy ^ 2 \times 6y \div 3xy$を計算せよ.
④$(x - 7)(x - 4) + 8x$を計算せよ.
⑤1次方程式$x + 4 = 5(2x - 1)$を解け.
⑥2次方程式$x ^ 2 + 3x - 18 = 0$を解け.
⑦$2\lt \sqrt a \lt \dfrac{10}{3}$をみたす正の整数のは何個あるか.
⑧図1で,2直線$\ell,m$は平行であり,
$\triangle ABC$は$AB = AC$の二等辺三角形である.
また,頂点$A,C$はそれぞれ $\ell m$上にある.
$\angle x$の大きさを求めよ.
⑨図2は,底面の半径が$3cm$,母線の長さが$ 9cm$の円すいである.
この円すいの体積を求めよ.ただし,円周率は$\pi$とする.
⑩図3は,女子生徒20人のハンドボール投げの記録をヒストグラムに表したもので,
平均値は12.2mであった.
このヒストグラムから読み取れることについて述べた次のア~エのうち,
正しいものをすべて選び,その記号を書け.
ア 中央値 (メジアン) は,平均値よりも小さい.
イ 最頻値(モード)は,平均値よりも大きい.
ウ 記録が12m未満の生徒は,全体の半数以上である.
工 記録が16m以上の生徒は,全体の20%である.
⑪図4で,数直線上を動く点$P$は,最初,原点$O$にある.
点$P$は,1枚の硬貨を1回投げるごとに,表が出れば正の方向に2だけ移動し,
裏が出れば負の方向に1だけ移動する.
硬貨を3回投げて移動した結果,点$P$が原点$O$にある確率を求めよ.
図は動画内参照
投稿日:2017.02.07