 方程式
方程式
 方程式
方程式
ただの一次方程式

単元:
#数学(中学生)#中1数学#方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{9}+\frac{1}{153}+\frac{1}{425}+\frac{1}{825}+\frac{1}{1353}=20$を解け
この動画を見る
$\frac{1}{9}+\frac{1}{153}+\frac{1}{425}+\frac{1}{825}+\frac{1}{1353}=20$を解け
【中学数学】数学用語チェック絵本 中1の用語”せめて”これだけは覚えよう!!

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#比例・反比例#空間図形#資料の活用#文字と式#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
この動画を見る
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
【中学数学】数学用語チェック絵本 vol 3 方程式

【中学数学】方程式の基礎をどこよりも丁寧に 3-1【中1数学】

【数検3級】数学検定3級対策問題2~5

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#連立方程式#式の計算(展開、因数分解)#2次方程式#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
この動画を見る
中1数学「方程式の文章題⑦(割合の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑦~(割合の問題)
例1
何円か持って買い物に行きました。最初に所持金の3/7使い 次に残りの所持金の5/8を使ったら、90円残りました。
最初の所持金を求めなさい。(記述)
例2
ある中学校の昨年度の生徒数は360人でした。 今年度の男子は5%減り、女子は10%増えたので 全体で12人増えました。
今年度の男子を求めなさい。
この動画を見る
中1~第31回方程式の文章題⑦~(割合の問題)
例1
何円か持って買い物に行きました。最初に所持金の3/7使い 次に残りの所持金の5/8を使ったら、90円残りました。
最初の所持金を求めなさい。(記述)
例2
ある中学校の昨年度の生徒数は360人でした。 今年度の男子は5%減り、女子は10%増えたので 全体で12人増えました。
今年度の男子を求めなさい。
中1数学「方程式の文章題⑥(比の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑥~ (比の問題)
例1
兄と弟はシールを25枚ずつ持っています。
兄が弟から何枚かもらったので、兄と弟の枚数の比は4:1になりました。 兄は弟から何枚もらいましたか。
例2
姉と妹の所持金の比は8:5でしたが、
姉は300円使い、妹は母から1000円もらったので、 姉と妹の所持金の比は9:8になりました。
妹の所持金は何円になりましたか。
この動画を見る
中1~第31回方程式の文章題⑥~ (比の問題)
例1
兄と弟はシールを25枚ずつ持っています。
兄が弟から何枚かもらったので、兄と弟の枚数の比は4:1になりました。 兄は弟から何枚もらいましたか。
例2
姉と妹の所持金の比は8:5でしたが、
姉は300円使い、妹は母から1000円もらったので、 姉と妹の所持金の比は9:8になりました。
妹の所持金は何円になりましたか。
中1数学「方程式の文章題⑤(年齢の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題⑤~ (年齢の問題)
例題
現在、子供は12才、父は42才です。
父の 年齢が子供の年齢の3倍になるのは、 今から何年後ですか。(記述)
この動画を見る
中1~第31回方程式の文章題⑤~ (年齢の問題)
例題
現在、子供は12才、父は42才です。
父の 年齢が子供の年齢の3倍になるのは、 今から何年後ですか。(記述)
中1数学「方程式の文章題④(速さの問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題④~(速さの問題)
例題
600m離れた学校に向かって、のぞみさんが家を出発しました。 その5分後に忘れ物に気づいたお母さんが自転車で追いかけました。
のぞみさんは、分速60m、お母さんは分速210 mで進む とき お母さんは出発してから何分後にのぞみさんに追いつきますか。
この動画を見る
中1~第31回方程式の文章題④~(速さの問題)
例題
600m離れた学校に向かって、のぞみさんが家を出発しました。 その5分後に忘れ物に気づいたお母さんが自転車で追いかけました。
のぞみさんは、分速60m、お母さんは分速210 mで進む とき お母さんは出発してから何分後にのぞみさんに追いつきますか。
中1数学「方程式の文章題③(過不足の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題③~ (過不足の問題)
例1
あめを何人かの子供に配りました。
1人に3個ずつ配ると8個余り。1人に5個ずつ配ると10個不足します。
子供の人数とあめの個数を求めなさい。 (記述)
例2
生徒が長いす1脚に4人ずつ座ると20人座れず、1脚に5人ずつ座ると長いすがちょうど1肤除ります。
生徒の人数と長いすの数を求めなさい。
この動画を見る
中1~第31回方程式の文章題③~ (過不足の問題)
例1
あめを何人かの子供に配りました。
1人に3個ずつ配ると8個余り。1人に5個ずつ配ると10個不足します。
子供の人数とあめの個数を求めなさい。 (記述)
例2
生徒が長いす1脚に4人ずつ座ると20人座れず、1脚に5人ずつ座ると長いすがちょうど1肤除ります。
生徒の人数と長いすの数を求めなさい。
中1数学「方程式の文章題②(代金の問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題②~(代金の問題)
例題
1個80円のりんごと1個60円のみかんを合わせて20個買ったら、 代金の合計は1340円でした。
りんごとみかんの個数を求めなさい。
この動画を見る
中1~第31回方程式の文章題②~(代金の問題)
例題
1個80円のりんごと1個60円のみかんを合わせて20個買ったら、 代金の合計は1340円でした。
りんごとみかんの個数を求めなさい。
中1数学「方程式の文章題①(数に関する問題)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第31回方程式の文章題①~(数に関する問題)
例1
ある数の4倍から1をひいた数は、もとの数の6倍よりも15小さい。
ある数を求めなさい。
例2
連続する3つの整数の和が87のとき、一番小さい整数を求めなさい。
例3
十の位の数が3の2けたの整数について、十の位と一の位を入れかえると、もとの数より45大きくなります。
もとの2けたの整数を求めなさい。
この動画を見る
中1~第31回方程式の文章題①~(数に関する問題)
例1
ある数の4倍から1をひいた数は、もとの数の6倍よりも15小さい。
ある数を求めなさい。
例2
連続する3つの整数の和が87のとき、一番小さい整数を求めなさい。
例3
十の位の数が3の2けたの整数について、十の位と一の位を入れかえると、もとの数より45大きくなります。
もとの2けたの整数を求めなさい。
中1数学「解が分かっている方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第30回解が分かっている方程式~
例1
Xについての方程式ax-8=2Xの解が-2のとき、aの値を求めなさい。
例2
Xについての方程式x+a/3-1=a-x/2の解がー2のとき、aの値を求めなさい。
この動画を見る
中1~第30回解が分かっている方程式~
例1
Xについての方程式ax-8=2Xの解が-2のとき、aの値を求めなさい。
例2
Xについての方程式x+a/3-1=a-x/2の解がー2のとき、aの値を求めなさい。
中1数学「比例式と方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第29回 比例式と方程式~
例題
次の比例式を解きなさい。
(1)X: 9 = 7 : 3 (2)6:5 = x :(1/3)
(3)X: (X+4)=2:3 (4) 3: (x + 2) = 4: (2x + 1)
この動画を見る
中1~第29回 比例式と方程式~
例題
次の比例式を解きなさい。
(1)X: 9 = 7 : 3 (2)6:5 = x :(1/3)
(3)X: (X+4)=2:3 (4) 3: (x + 2) = 4: (2x + 1)
中1数学「小数をふくむ方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第28回小数をふくむ方程式~
例題
次の方程式を解きなさい。
(1) 1 - 0.9x = 4.6
(2) 0.3 - 0.13x = - 0.08x
(3) 0.3(x - 1.5) = 0.2x +1
(4)2-(x+2)/3=0,6(1+x)
この動画を見る
中1~第28回小数をふくむ方程式~
例題
次の方程式を解きなさい。
(1) 1 - 0.9x = 4.6
(2) 0.3 - 0.13x = - 0.08x
(3) 0.3(x - 1.5) = 0.2x +1
(4)2-(x+2)/3=0,6(1+x)
中1数学「分数をふくむ方程式」【毎日配信】

中1数学「かっこのある方程式」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第26回 かっこのある方程式~
例題
次の方程式を解きなさい。
(1)3(x - 4) = 5x + 4 (2) 6x - 5(x - 1) = 8
(3) 2(x - 1) = 4(x - 3) (4)5-(x-3)=1+(-2x+1)
この動画を見る
中1~第26回 かっこのある方程式~
例題
次の方程式を解きなさい。
(1)3(x - 4) = 5x + 4 (2) 6x - 5(x - 1) = 8
(3) 2(x - 1) = 4(x - 3) (4)5-(x-3)=1+(-2x+1)
中1数学「方程式とその解き方②(移項)」【毎日配信】

中1数学「方程式とその解き方①(等式の性質)」【毎日配信】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
方程式とその解き方①(等式の性質)に関して解説していきます。
この動画を見る
方程式とその解き方①(等式の性質)に関して解説していきます。
【中1 数学】 1-②⑤ 方程式って?
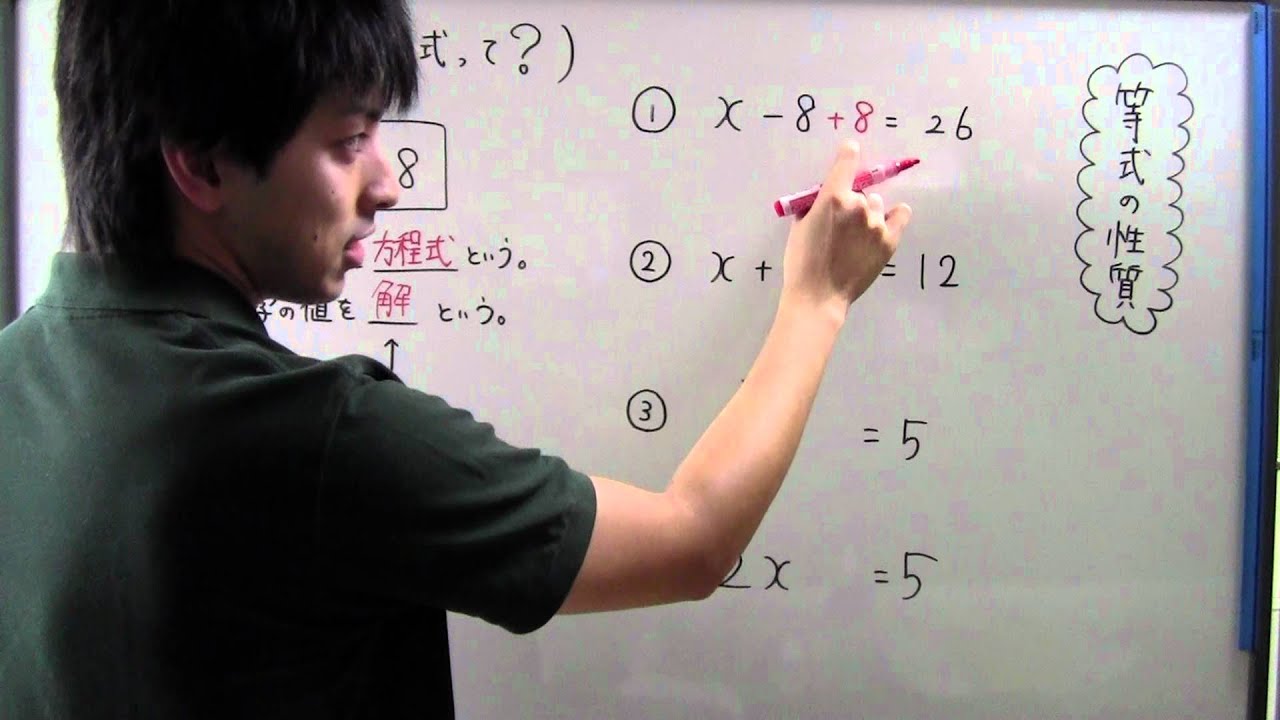
単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 方程式って?
[解説]
3x+7=28
文字をふくむ等式を( )という。
あてはまる文字の値を( )という。
これを求めることを( )という。
[問題]
次の方程式を解け。
① x - 8 = 26
② x + 3 = 12
③ $\frac{x}{9} = 5$
④ 2x = 5
この動画を見る
中1 数学 方程式って?
[解説]
3x+7=28
文字をふくむ等式を( )という。
あてはまる文字の値を( )という。
これを求めることを( )という。
[問題]
次の方程式を解け。
① x - 8 = 26
② x + 3 = 12
③ $\frac{x}{9} = 5$
④ 2x = 5
【中1 数学】 1-①⑨ 等式と不等式 【6~7月】

単元:
#数学(中学生)#中1数学#方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
中1 数学 等式と不等式
等式 $ 5x - y = 27$
不等式 $ 5x - y \gt 27$
以下の問を式に表せ
[等式]
① $x$ 円のケーキ $3$ つを $30$ 円の ラッピングをしてもらうと $720$ 円です。
② $1000$ 円で $a$ 円のりんごを $4$ つ買うと、おつりは $440$ 円でした。
[不等式]
③ $4$ 人で $x$ 円ずつ出すと、$1500$ 円以上になる。
④ $x$ から $5$ をひくと、$2$ より小さい。
この動画を見る
中1 数学 等式と不等式
等式 $ 5x - y = 27$
不等式 $ 5x - y \gt 27$
以下の問を式に表せ
[等式]
① $x$ 円のケーキ $3$ つを $30$ 円の ラッピングをしてもらうと $720$ 円です。
② $1000$ 円で $a$ 円のりんごを $4$ つ買うと、おつりは $440$ 円でした。
[不等式]
③ $4$ 人で $x$ 円ずつ出すと、$1500$ 円以上になる。
④ $x$ から $5$ をひくと、$2$ より小さい。
