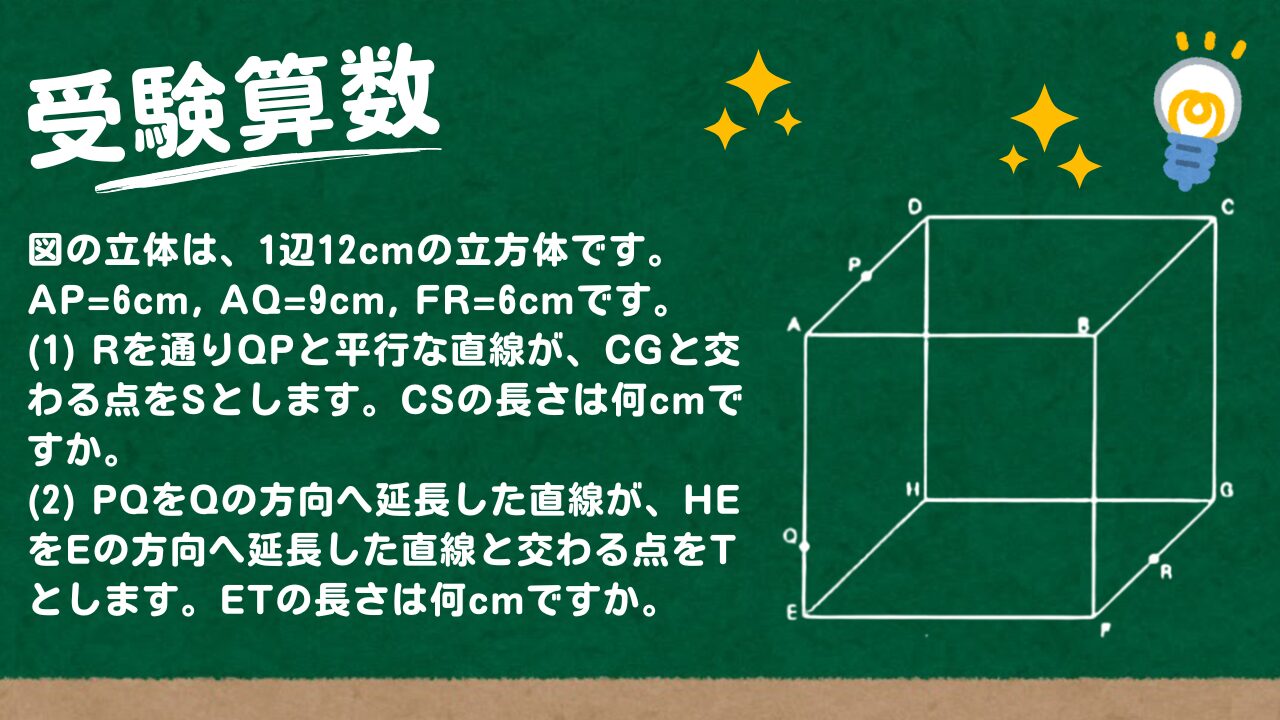
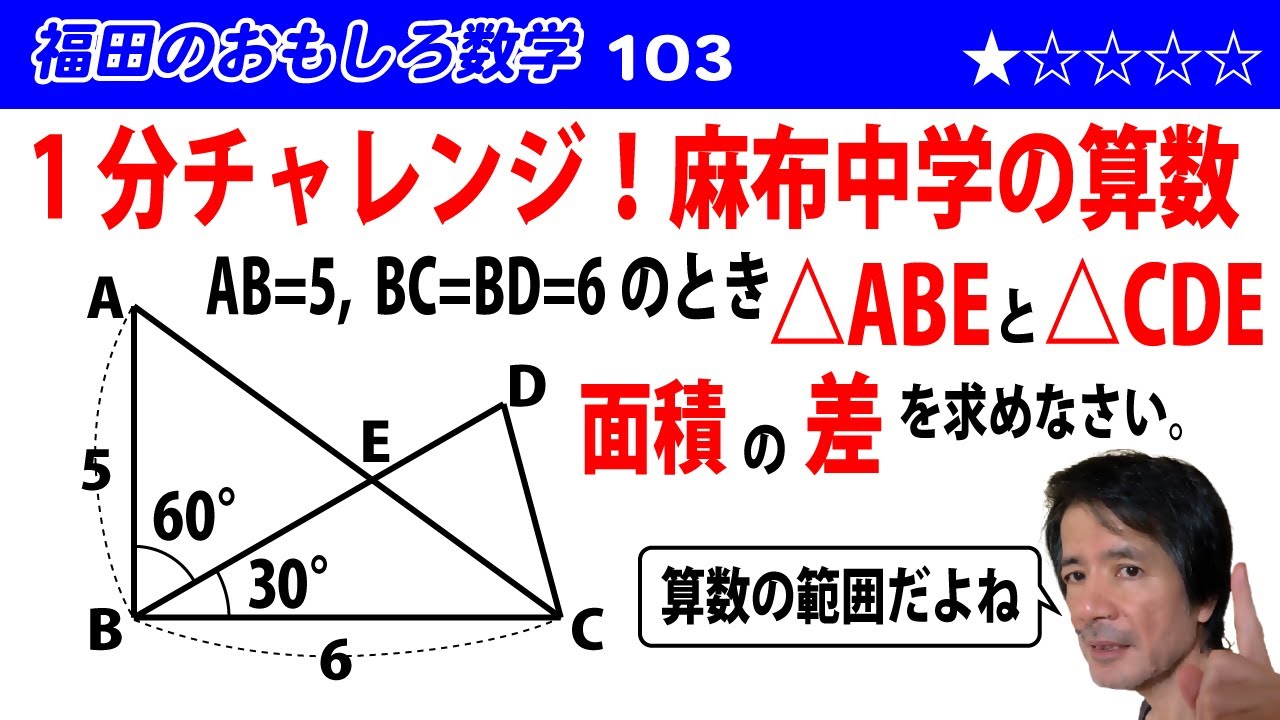
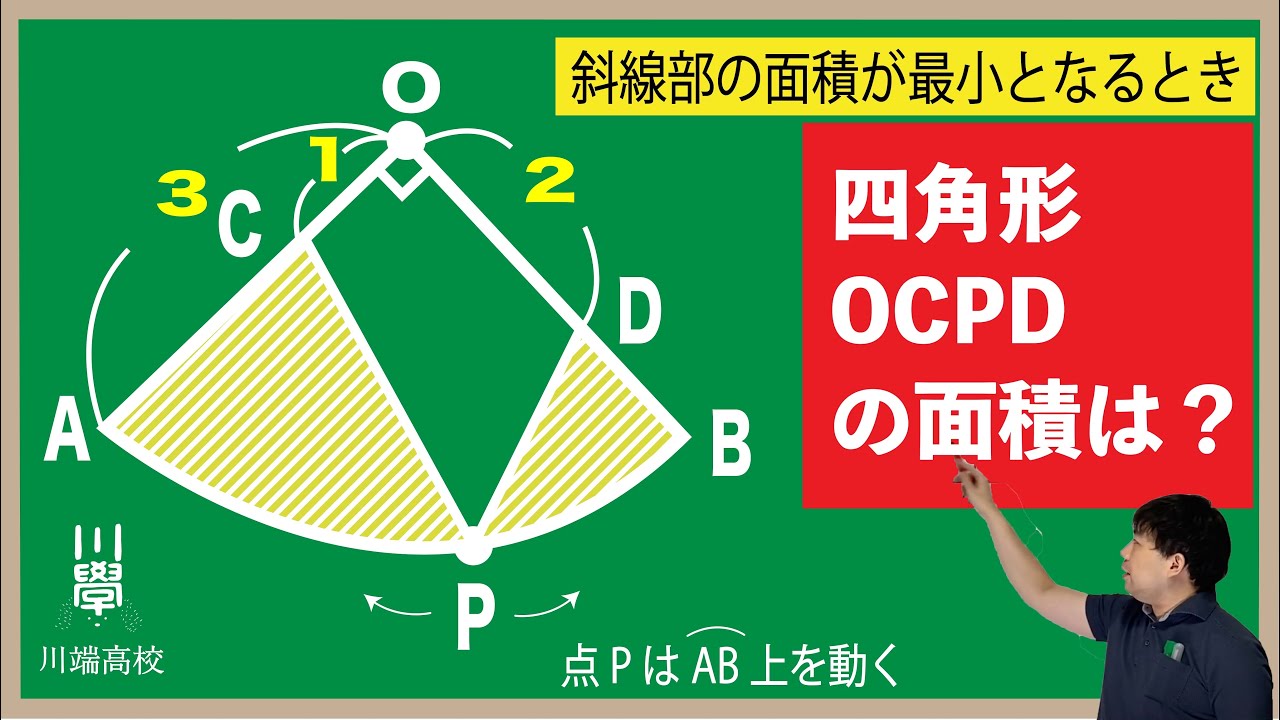
問題文全文(内容文):
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
単元:
#算数(中学受験)#過去問解説(学校別)#海城中学
指導講師:
重吉
問題文全文(内容文):
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
次の問いに答えなさい。
(1)9÷[4{1/6} +{2.25-1(1/2)}/0.75-2{1/2}]/1.125
(2) 8%の食塩水80g, 6%の食塩水120g,4%の食塩水150g,水▭gを混ぜて5%の食塩水をつくりました。▭にあてはまる数を求めなさい。
(3)現在、父の年齢は兄の年齢の3倍と弟の年齢の和より4歳上です。24年後, 父の年齢は兄と弟の年齢の和に等しくなります。父と弟の年齢の差を求めなさい。
(4)100以上300以下の整数のうち、約数の個数が9個である整数をすべて求めなさい。
(5) 下の図において直線ABとCDは平行で、長さの等しい辺には同じ印がついています。図の角アの大きさを求めなさい。*図は動画内参照
投稿日:2024.09.23