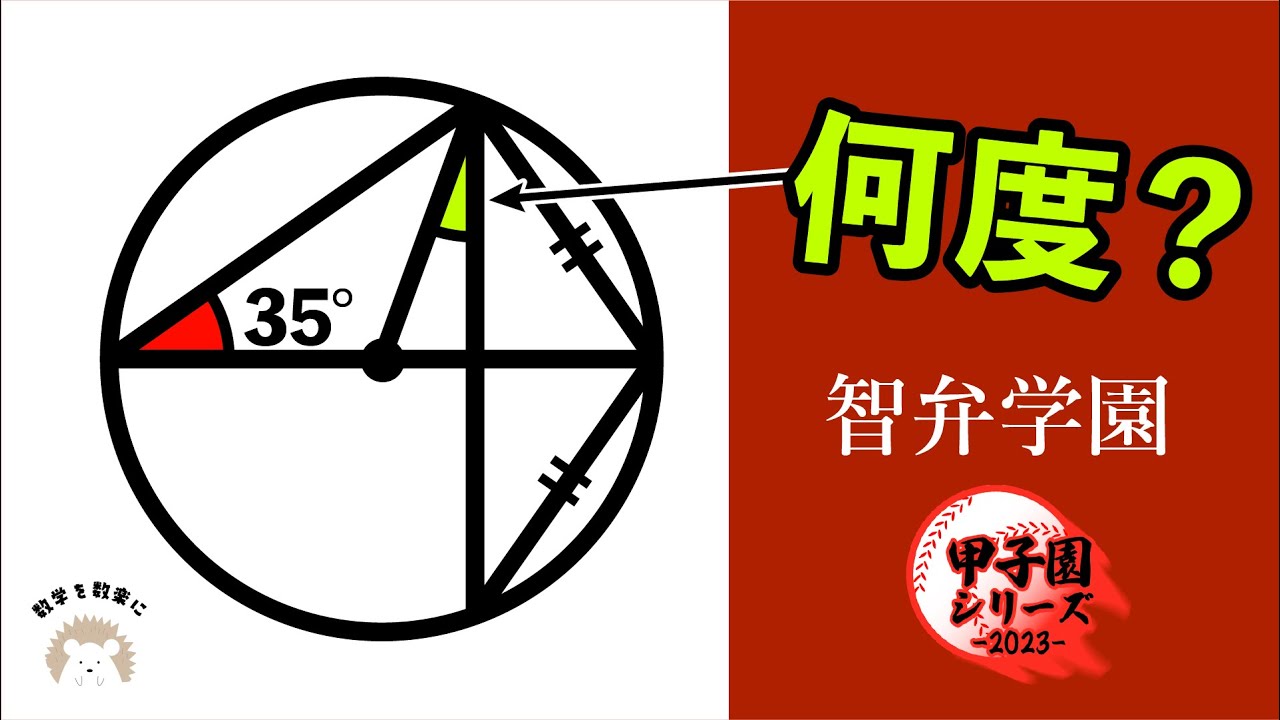
問題文全文(内容文):
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
単元:
#数Ⅰ#数A#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
(1)
ストライドを$x$、ピッチを$z$とおく。
ピッチは1秒あたりの少数、ストライドは1歩あたりの進む距離なので、1秒あたりの進む距離すなわち平均速度は、$x$と$z$を用いて[ア](m/秒)と表される。
これより、タイムと、ストライド、ピッチとの関係は
タイム=$\displaystyle \frac{100}{[ア]}$
と表されるので、[ア]が最大になるときにタイムが最もよくなる。
ただし、タイムがよくなるとは、タイムの値が小さくなることである。
[ア]を以下から選べ。
⓪$x+z$
①$z-x$
②$xz$
③$\displaystyle \frac{x+z}{[2]}$
④$\displaystyle \frac{z-x}{[2]}$
⑤$\displaystyle \frac{xz}{[2]}$
(2)
男子短距離100m走の選手である太郎さんは、①に着目して、タイムが最もよくなるストライドとピッチを考えることにした。
次の表は、太郎さんが練習で100mを3回走ったときのストライドとピッチのデータである。
-----------------
1回目 2回目 3回目
ストライド 2.05 2.10 2.15
ピッチ 4,70 4.60 4.50
-----------------
また、ストライドとピッチにはそれぞれ限界がある。
太郎さんの場合、ストライドの最大値は2.40、ピッチの最大値は4.80である。
太郎さんは、上の表から、ストライドが0.05大きくなるとピッチが0.1小さくなるという関係があると考えて、ピッチがストライドの1次関数としてなされると仮定した。
このとき、ピッチ$z$はストライド$x$を用いて
$z=[イウ]x+\displaystyle \frac{[エオ]}{5}$ と表される。
②が太郎さんのストライドの最大値2.40とピッチの最大値4.80まで成り立つと仮定すると、$x$の値の範囲は次のようになる。
$[カ].[キク]\leqq x \leqq 2.40$
$y=[ア]$とおく。
②を$y=[ア]$に代入することにより、$y$と$x$の関数として表すことができる。
太郎さんのタイムが最もよくなるストライドとピッチを求めるためには、$[カ].[キク]\leqq x \leqq 2.40$の範囲で$y$の値を最大にする$x$の値を見つければよい。
このとき、$y$の値が最大になるのは$x=[ケ].[コサ]$のときである。
よって、太郎さんのタイムが最もよくなるのは、ストライドが[ケ].[コサ]のときであり、このとき、ピッチは[シ].[スセ]である。
このときの太郎さんのタイムは①により[ソ]である。
[ソ]については、最も適当なものを、次の⓪~⑤のうちから、一つ選べ。
⓪9.68
①9.97
②10.09
③10.33
④10.42
⑤10.55
投稿日:2021.12.27