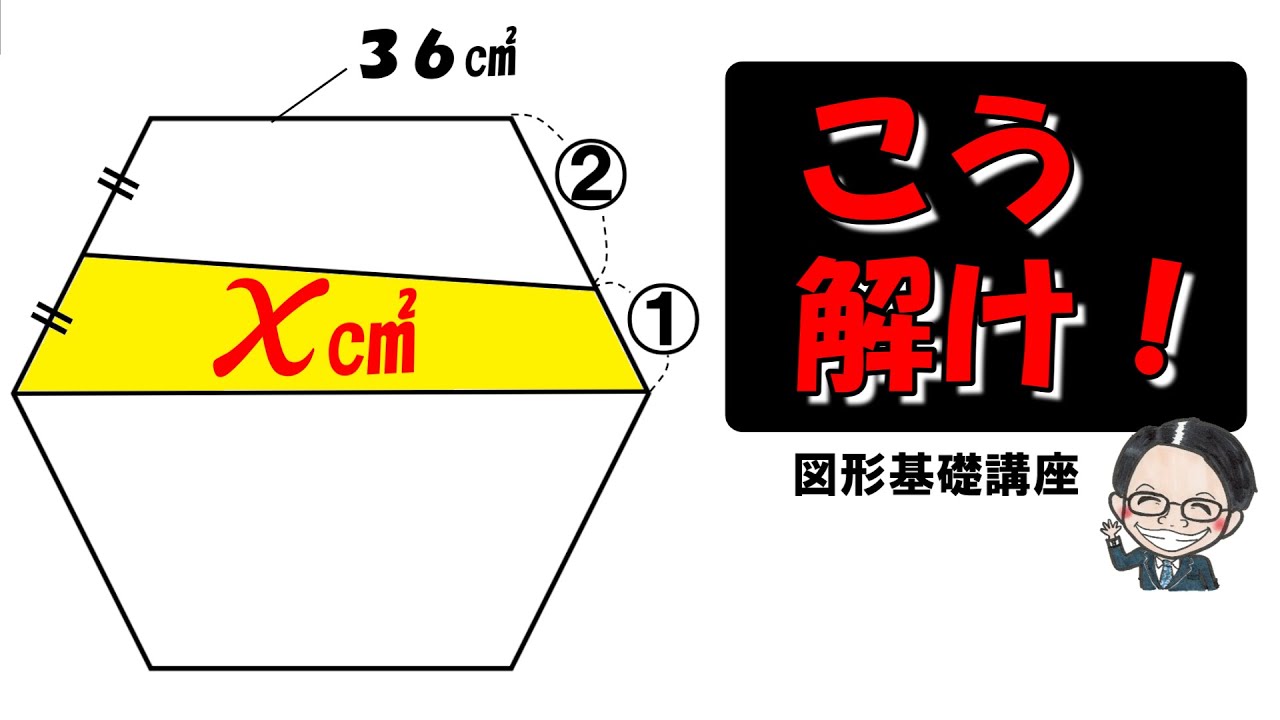
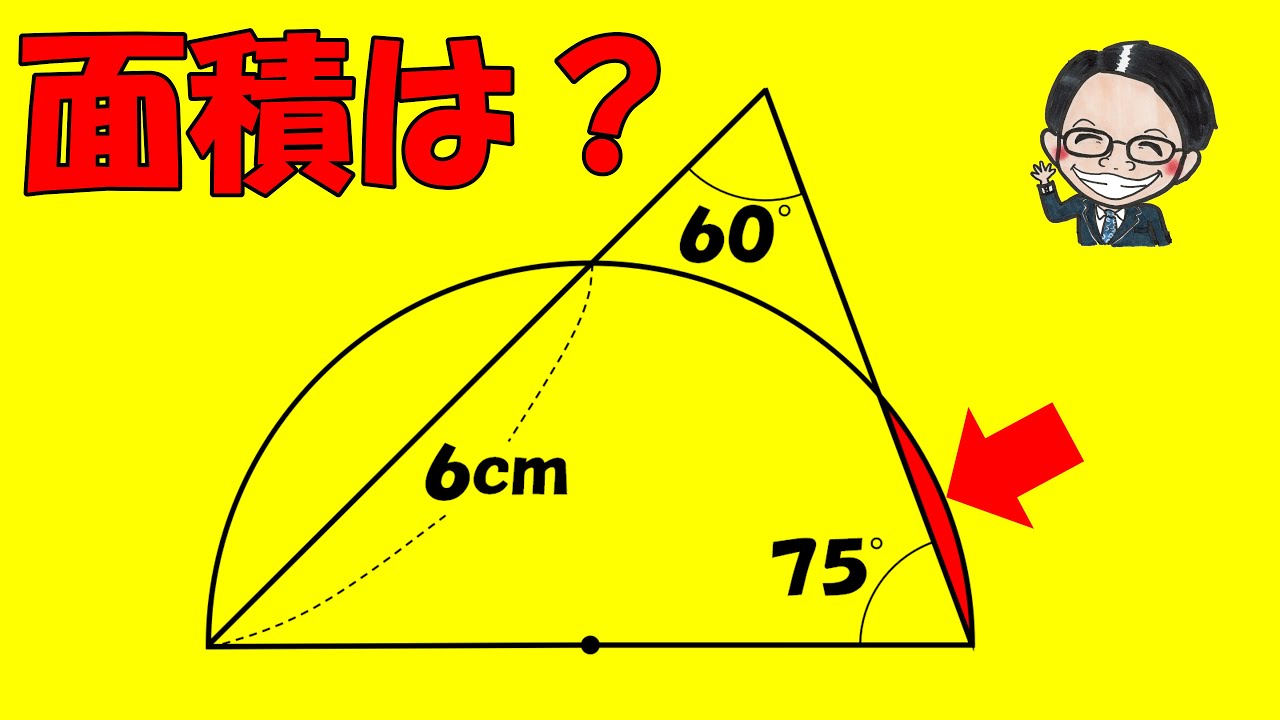
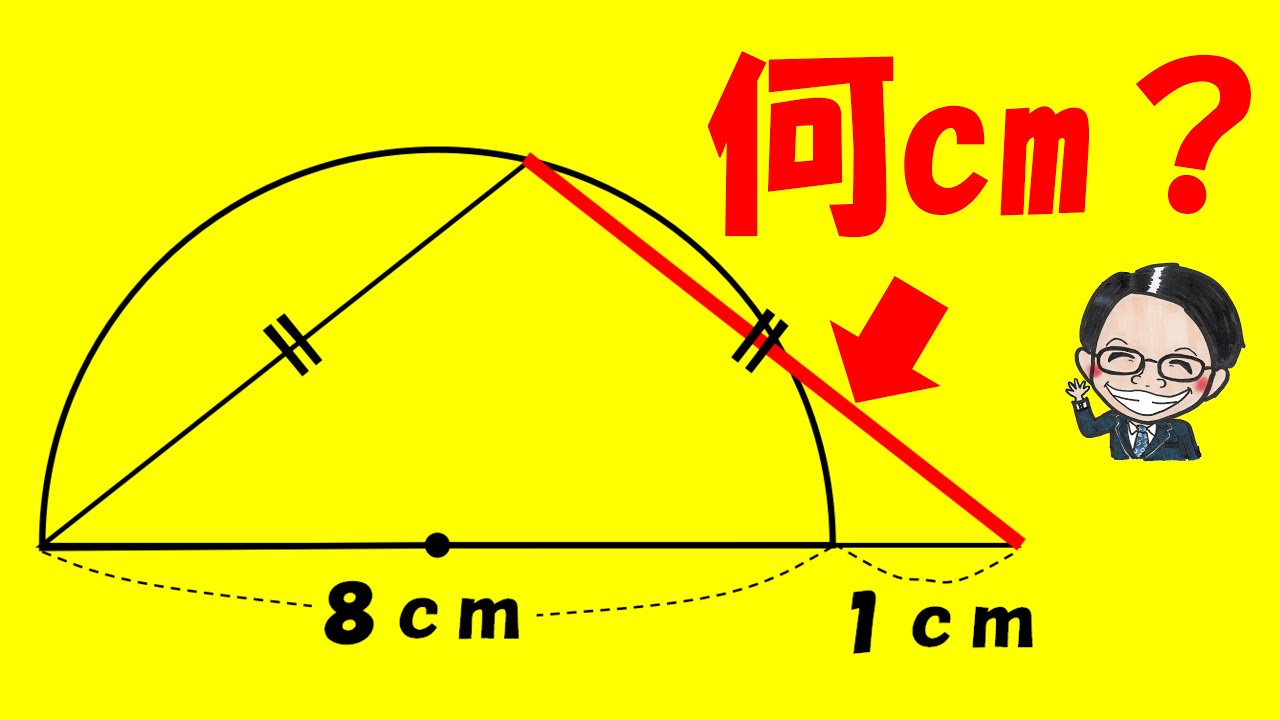
問題文全文(内容文):
ご石を図1のように並べて、正三角形を作っていきます。一番下のご石が2個、3個、4個のとき、ご石の数は全部で、それぞれ3個、6個、10個です。次に、正三角形のいちばん下のご石にそろえて図2のように並べていきます。次の□にあてはまる数を求めなさい。
(1)図1のような並べ方で、いちばん下のご石が12個のとき、ご石の数は全部で□個です。
(2)図2のような並べ方で、いちばん上のご石が13個のとき、ご石の数は全部で(あ)個か、(い)個です。
ご石を図1のように並べて、正三角形を作っていきます。一番下のご石が2個、3個、4個のとき、ご石の数は全部で、それぞれ3個、6個、10個です。次に、正三角形のいちばん下のご石にそろえて図2のように並べていきます。次の□にあてはまる数を求めなさい。
(1)図1のような並べ方で、いちばん下のご石が12個のとき、ご石の数は全部で□個です。
(2)図2のような並べ方で、いちばん上のご石が13個のとき、ご石の数は全部で(あ)個か、(い)個です。
チャプター:
0:00 オープニング
0:02 1)
1:44 2)
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ご石を図1のように並べて、正三角形を作っていきます。一番下のご石が2個、3個、4個のとき、ご石の数は全部で、それぞれ3個、6個、10個です。次に、正三角形のいちばん下のご石にそろえて図2のように並べていきます。次の□にあてはまる数を求めなさい。
(1)図1のような並べ方で、いちばん下のご石が12個のとき、ご石の数は全部で□個です。
(2)図2のような並べ方で、いちばん上のご石が13個のとき、ご石の数は全部で(あ)個か、(い)個です。
ご石を図1のように並べて、正三角形を作っていきます。一番下のご石が2個、3個、4個のとき、ご石の数は全部で、それぞれ3個、6個、10個です。次に、正三角形のいちばん下のご石にそろえて図2のように並べていきます。次の□にあてはまる数を求めなさい。
(1)図1のような並べ方で、いちばん下のご石が12個のとき、ご石の数は全部で□個です。
(2)図2のような並べ方で、いちばん上のご石が13個のとき、ご石の数は全部で(あ)個か、(い)個です。
投稿日:2024.08.18