東大2020文系第2問 ヨビノリたくみ＆東大受験芸人たわし - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数Ⅰ > 東大2020文系第2問　ヨビノリたくみ＆東大受験芸人たわし

東大2020文系第2問　ヨビノリたくみ＆東大受験芸人たわし

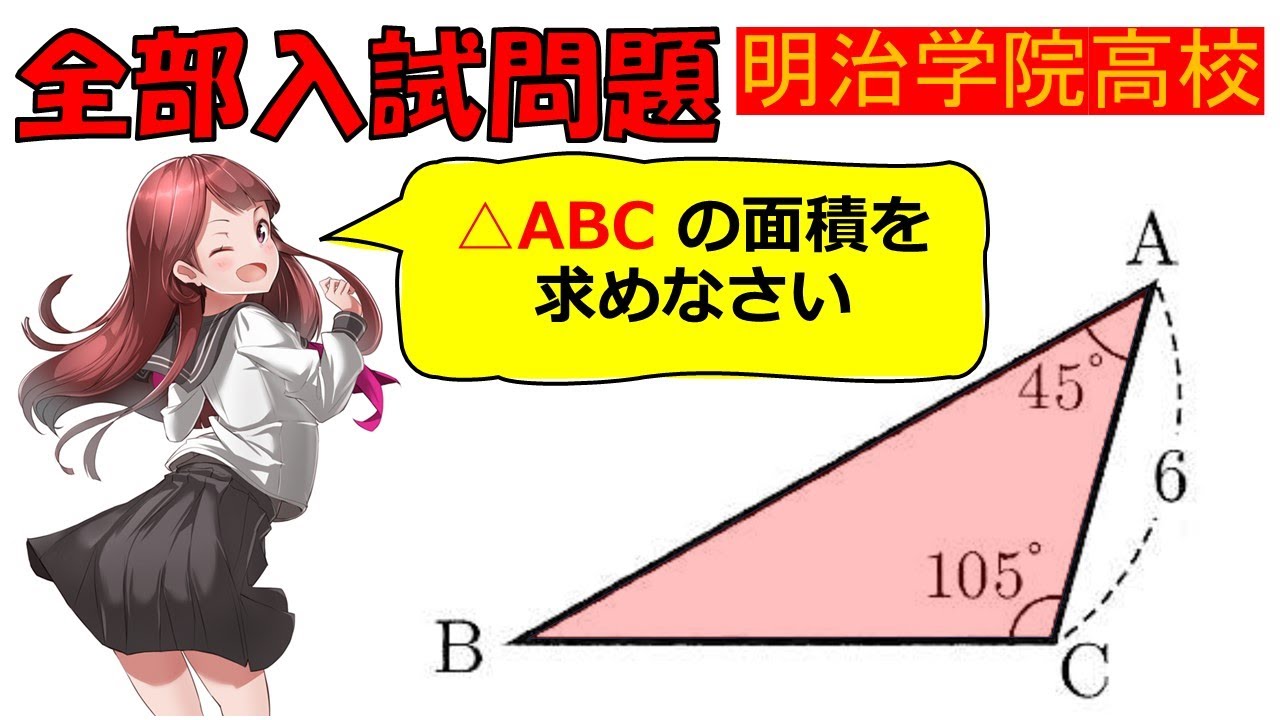
問題文全文(内容文)：
4本の直線が縦横に引かれている
交わる箇所の点は16個
この点の中から5個選ぶ
（1）
5個選んだ時に、その点を通らない直線がちょうど2つになる場合の確率を求めよ

（2）
どの直線も少なくとも1つ通る場合の確率を求めよ

出典：2020年東京大学　文系第2問
単元： #数Ⅰ#数A#場合の数と確率#場合の数#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
4本の直線が縦横に引かれている
交わる箇所の点は16個
この点の中から5個選ぶ
（1）
5個選んだ時に、その点を通らない直線がちょうど2つになる場合の確率を求めよ

（2）
どの直線も少なくとも1つ通る場合の確率を求めよ

出典：2020年東京大学　文系第2問
投稿日：2020.03.24

＜関連動画＞

東大　２次方程式　解と係数　漸化式 Mathematics Japanese university entrance exam

アイキャッチ画像
単元： #数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$x^2-4x-1=0$の2つの解を$\alpha, \beta(a \gt \beta),S_{n}=\alpha ^n+\beta ^n$

（1）
$S_{1},S_{2},S_{3}$を求めよ。
$S_{n}$を$S_{n-1}$と$S_{n-2}$で表せ

（2）
$\beta^3$以下の最大の整数を求めよ

（3）
$a^{2003}$以下の最大の整数の1の位の数を求めよ

出典：2003年東京大学　過去問
この動画を見る　

Jr. Japan Mathematics Olympiad 1st round

アイキャッチ画像
単元： #数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学オリンピック#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
$x+\sqrt{x(x+1)} + x+\sqrt{x(x+2)} + x+$
$\sqrt{x(x+1)(x+2)}=2$ solve x(only the positive real number one)
この動画を見る　

【数学Ⅰ/三角比】円に内接する四角形②

アイキャッチ画像
単元： #数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)
指導講師： 【ゼロから理解できる】高校数学・物理
問題文全文(内容文)：
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。

（1）
$\cos\angle ABC$

（2）
対角線$AC$の長さ

（3）
四角形$ABCD$の面積$S$
この動画を見る　

３乗根と平方根の方程式

アイキャッチ画像
単元： #数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
これを解け.

$\sqrt[3]{4-x^2}+\sqrt{x^2-3}=1$
この動画を見る　

福田のおもしろ数学577〜条件付きの最大を求める

アイキャッチ画像
単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：

$2x^2+3y^2+4z^2=1$のとき

$5x-6y+7z$の最大値と

そのときの$x,y,z$を求めよ。
　　　　
この動画を見る　
PAGE TOP