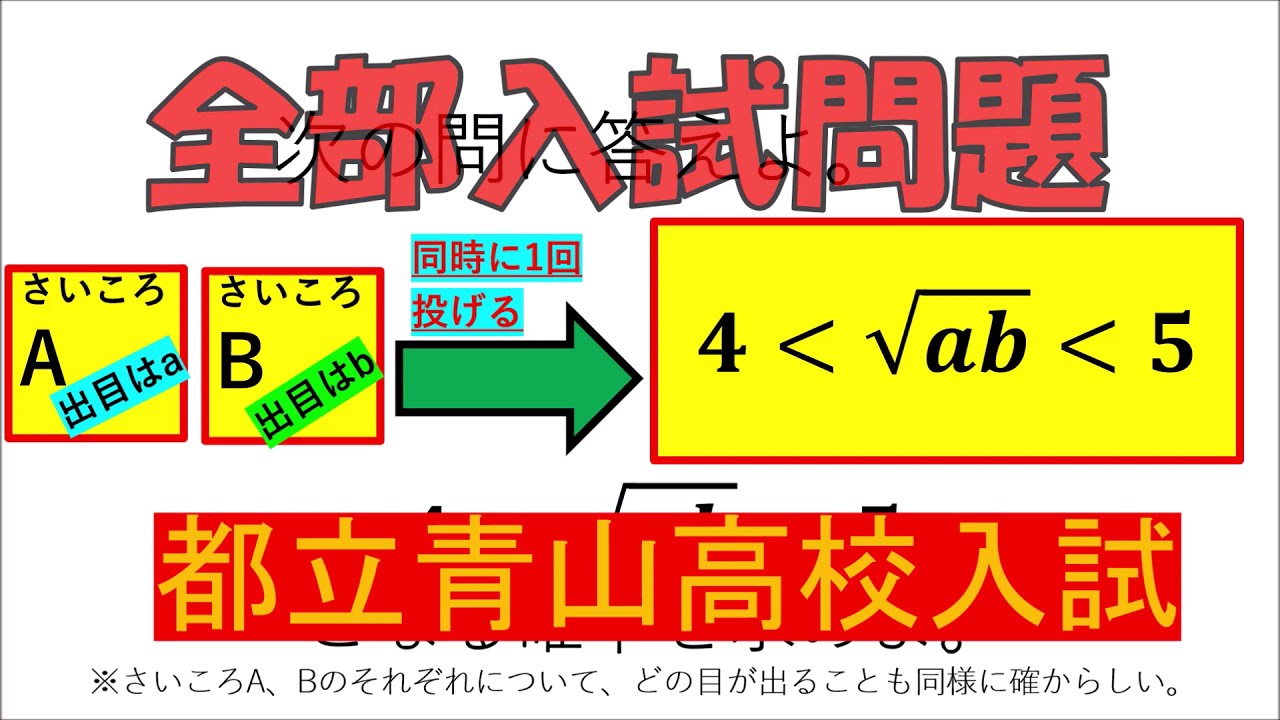
問題文全文(内容文):
①ゆきさんは、Tシャツとスカートを$1$組買いました。
定価で買うと$4800$円のところを、
Tシャツを定価の$2$割引き、
スカートを定価の$30%$引きで買ったので
$3540$円でした。
それぞれの定価はいくら?
②$12%$の食塩水と$7%$の食塩水を混ぜ合わせて、$10%$の食塩水を$500g$つくります。
$2$種類の食塩水をそれぞれ何$g$ずつ混ぜればいい?
①ゆきさんは、Tシャツとスカートを$1$組買いました。
定価で買うと$4800$円のところを、
Tシャツを定価の$2$割引き、
スカートを定価の$30%$引きで買ったので
$3540$円でした。
それぞれの定価はいくら?
②$12%$の食塩水と$7%$の食塩水を混ぜ合わせて、$10%$の食塩水を$500g$つくります。
$2$種類の食塩水をそれぞれ何$g$ずつ混ぜればいい?
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①ゆきさんは、Tシャツとスカートを$1$組買いました。
定価で買うと$4800$円のところを、
Tシャツを定価の$2$割引き、
スカートを定価の$30%$引きで買ったので
$3540$円でした。
それぞれの定価はいくら?
②$12%$の食塩水と$7%$の食塩水を混ぜ合わせて、$10%$の食塩水を$500g$つくります。
$2$種類の食塩水をそれぞれ何$g$ずつ混ぜればいい?
①ゆきさんは、Tシャツとスカートを$1$組買いました。
定価で買うと$4800$円のところを、
Tシャツを定価の$2$割引き、
スカートを定価の$30%$引きで買ったので
$3540$円でした。
それぞれの定価はいくら?
②$12%$の食塩水と$7%$の食塩水を混ぜ合わせて、$10%$の食塩水を$500g$つくります。
$2$種類の食塩水をそれぞれ何$g$ずつ混ぜればいい?
投稿日:2013.05.24