【中学数学】立体の体積と表面積の求め方～どこよりも丁寧に～ 6-4【中１数学】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中１数学 > 空間図形 > 【中学数学】立体の体積と表面積の求め方～どこよりも丁寧に～ 6-4【中１数学】

【中学数学】立体の体積と表面積の求め方～どこよりも丁寧に～ 6-4【中１数学】

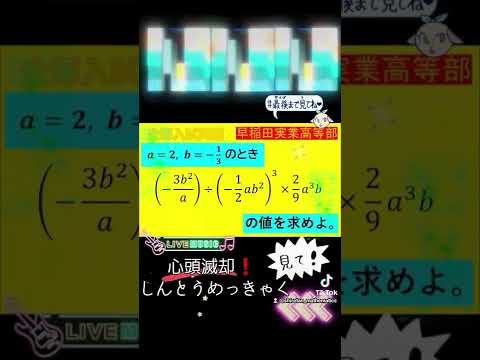
問題文全文(内容文)：
【中学数学】～どこよりも丁寧に～ 6-4【中１数学】
「立体の体積と表面積の求め方」について解説しています。
単元： #数学(中学生)#中１数学#空間図形
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
【中学数学】～どこよりも丁寧に～ 6-4【中１数学】
「立体の体積と表面積の求め方」について解説しています。
投稿日：2024.06.21

＜関連動画＞

【ケアレスミスをなくすには…！】計算：江戸川学園取手高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中１数学#正の数・負の数#文字と式#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ -144a^4b^2c^3\div(-6a^3b^2c^2)^3\times \left(-\dfrac{3}{2}a^3b^2c\right)^2$を計算しなさい.

江戸川取手高校過去問
この動画を見る　

【全員集合！】図形：椙山女学園高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
四角形の集合どうしの関係について,図の()として最も適切なものを選びなさい.

椙山女学園高等学校過去問
この動画を見る　

中学レベル　図形問題

アイキャッチ画像
単元： #数学(中学生)#中１数学#平面図形
指導講師： 鈴木貫太郎
問題文全文(内容文)：
図形問題に関して解説していきます.
この動画を見る　

【中1 数学】中1-62 比例 ・ 反比例の利用⑧ ~歯車編 ~

アイキャッチ画像
単元： #数学(中学生)#中１数学#比例・反比例
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎Aの歯車の歯の数は56で、1分間に8回転する。
Bの歯車の歯の数はxで1分間にy回転する。

①yをXの式で表すと?

②Bの歯車の歯が32のとき、Bは1分間に何回転するかな？

③Bの歯車の代わりにCの歯車を取り付けると、5分間に35回転した。
Cの歯車の歯の数はいくつ？
※図は動画内参照
この動画を見る　

長方形は何こ？

アイキャッチ画像
単元： #数学(中学生)#中１数学#平面図形
指導講師： 数学を数楽に
問題文全文(内容文)：
長方形は何コある？
＊図は動画内参照
この動画を見る　
PAGE TOP