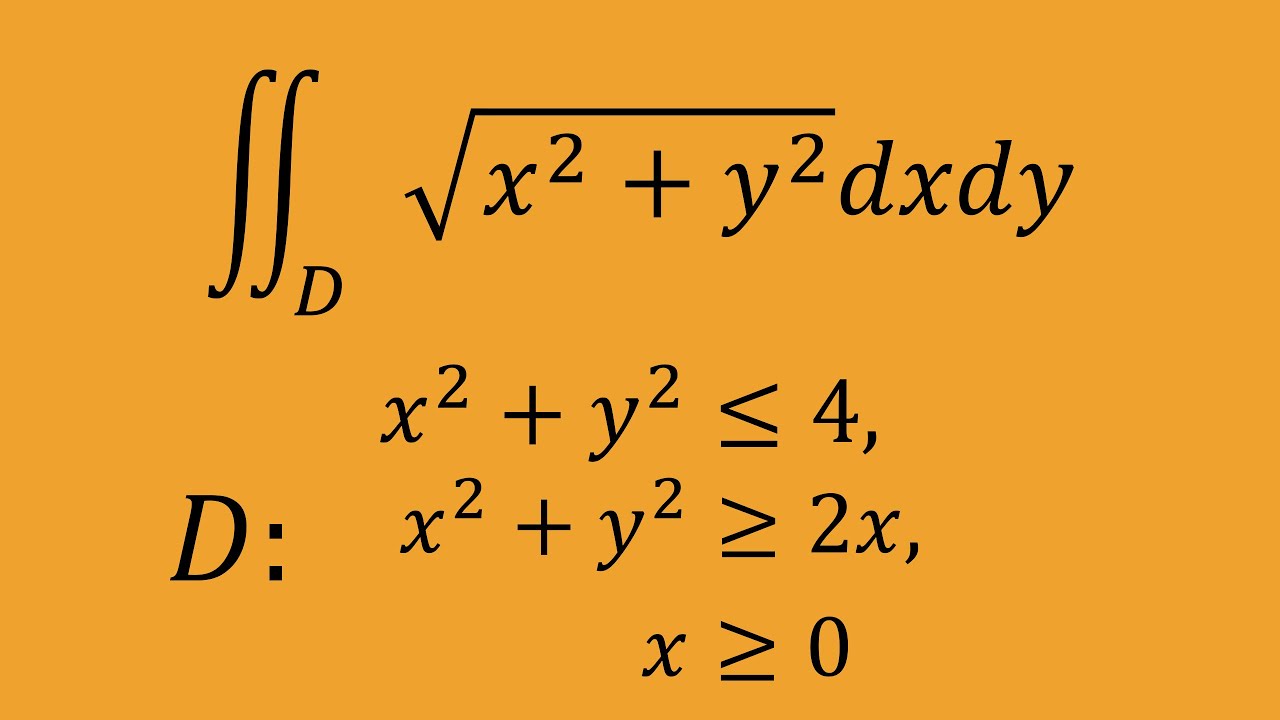問題文全文(内容文):
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
チャプター:
0:00 問題7について
2:56 (10)の解説
7:28 まとめ
単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定準2級#その他#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
投稿日:2023.05.22