問題文全文(内容文):
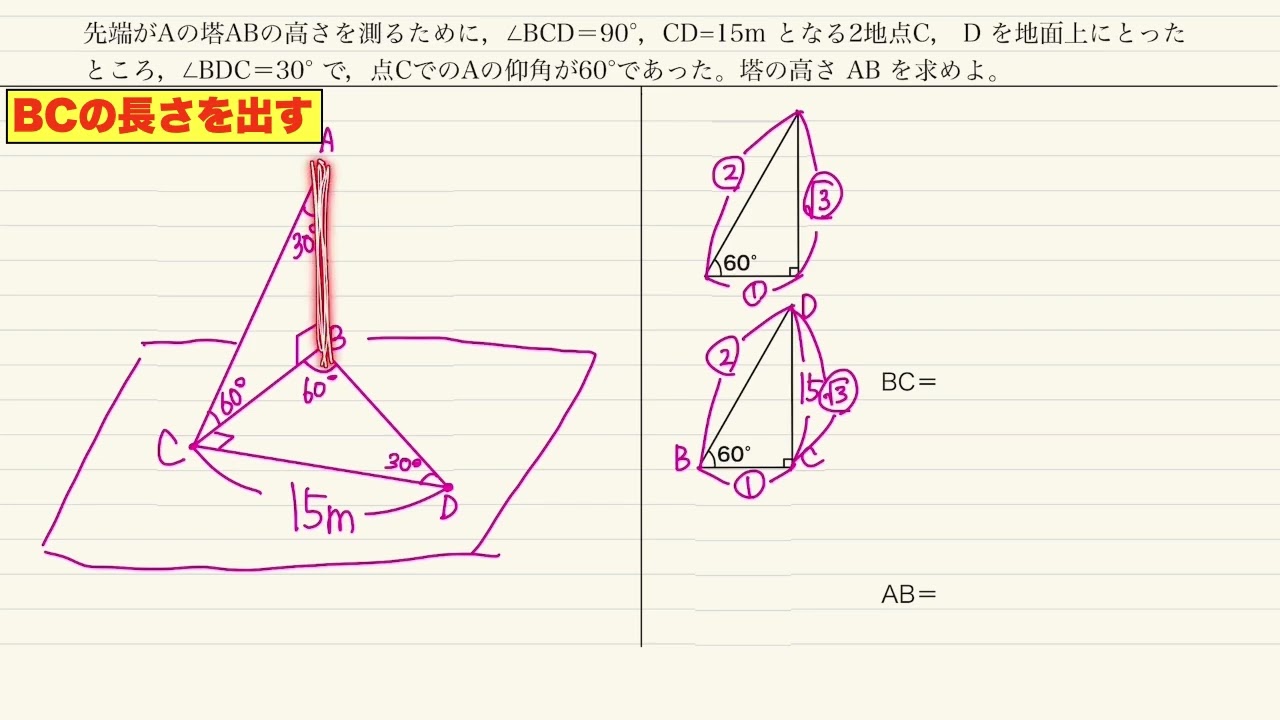
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
チャプター:
0:00 オープニング
0:05 問題文
0:20 アプローチ
1:09 解説(ADの長さ)
3:19 解説(AMの長さ)
4:32 エンディング
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、$AB=400m、BC=100\sqrt3 m,\angle QAB=30°,\angle PBA=\angle QBC=75°,\angle PCB=45°$であった。P、Q間の距離を求めよ。
投稿日:2023.04.20