え！？これだけの情報で解けるの？実は○○を使えば解けるんです！さあ、あなたは解けるかな？【中学受験算数】【入試問題】【西大和学園中】

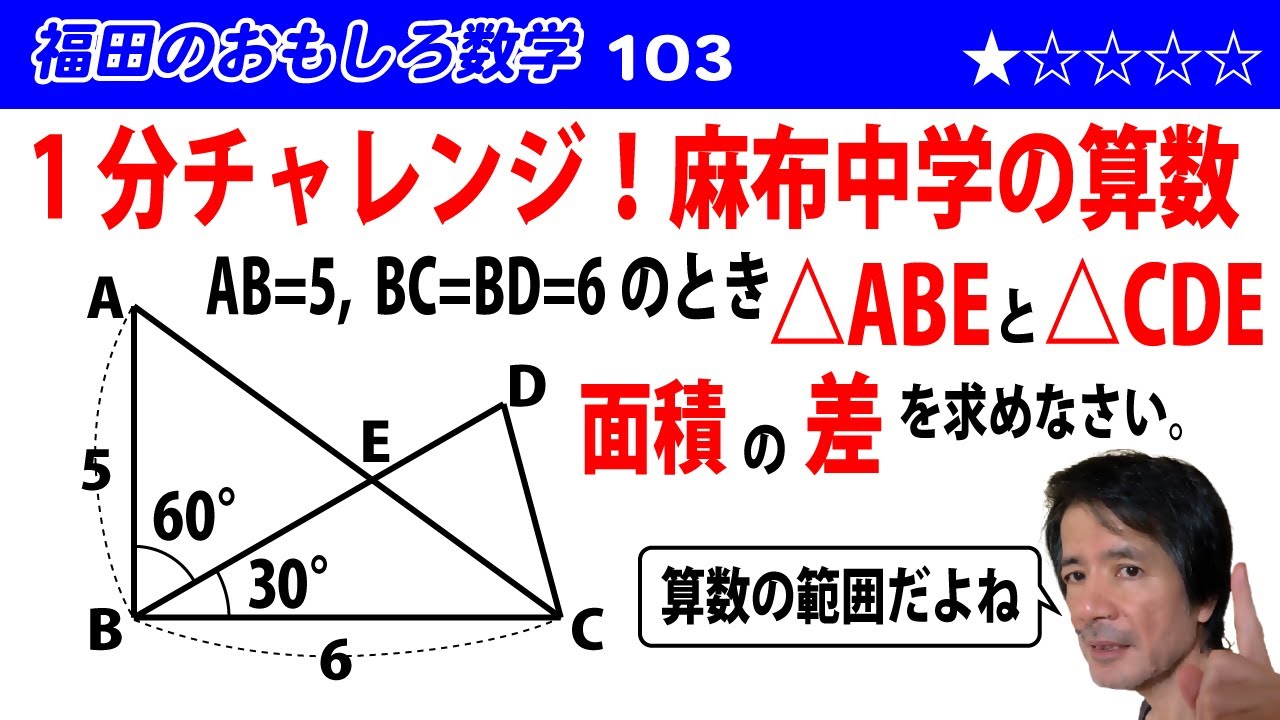
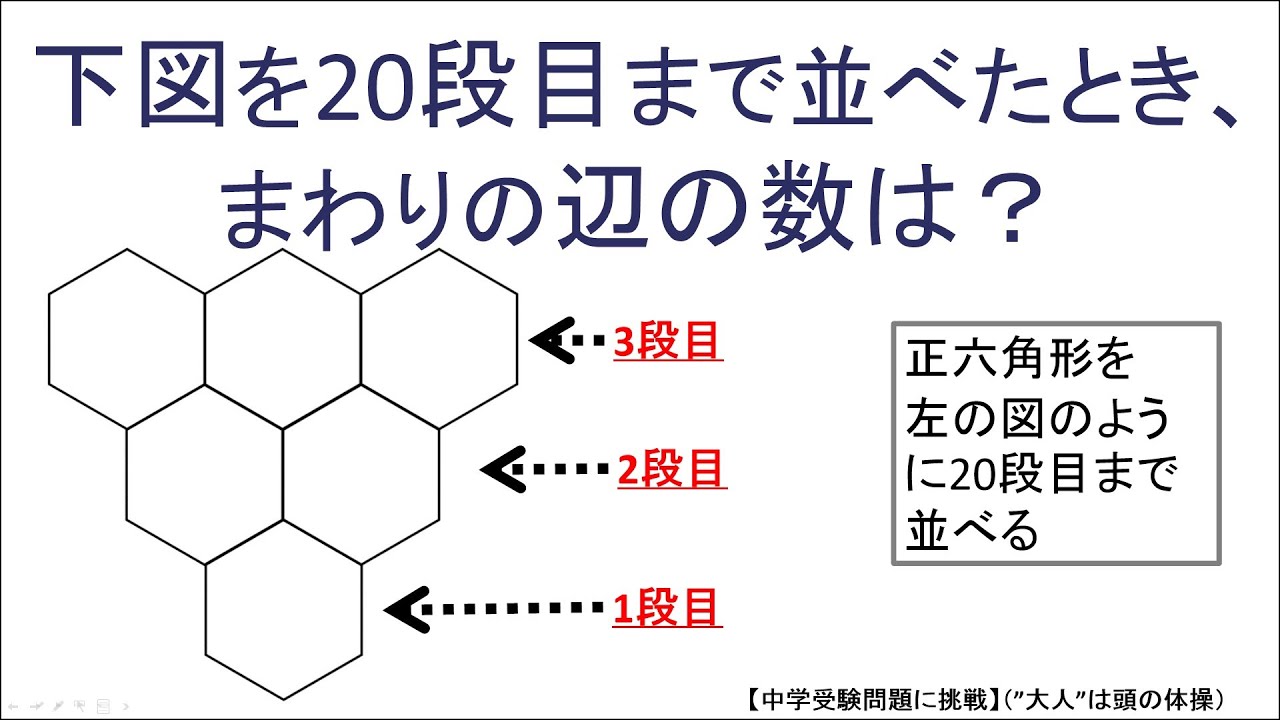
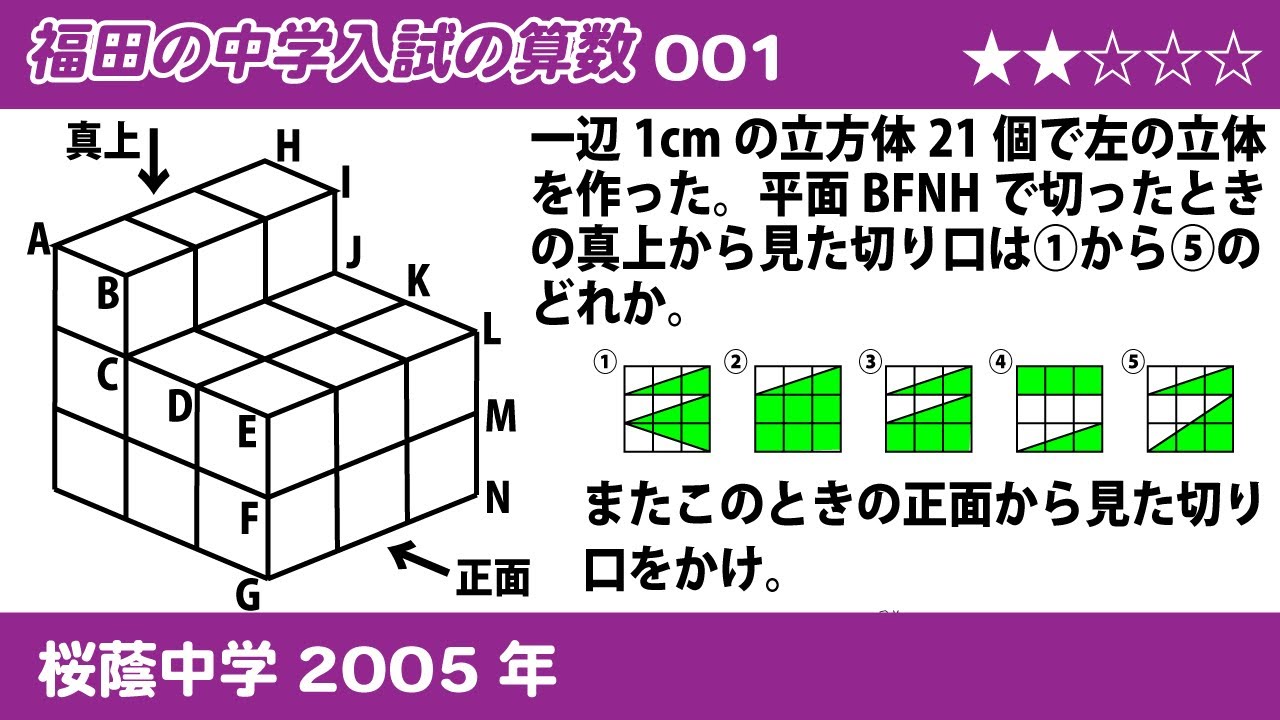
問題文全文(内容文)：
2022豊島岡女子学園中学校
左図の正方形ABCDで斜線部分の面積は？

2022西大和学園中学校
左図の四角形ABCDは正方形で、(ADの長さ)：(CEの長さ)＝12：5となるように辺BC上に点Eをとる。図の○のついた角の大きさが同じになるようにDE上に点FをとったとこりDFの長さが5㎝となった。
四角形ABEFの面積は？

＊図は動画内参照

チャプター：

0:00　オープニング
0:11　今日の内容説明
1:15　１問目　豊島岡女子学園中　問題提示
1:50　１問目　豊島岡女子学園中　問題解説
6:43　２問目　サムネイルの問題　西大和中　問題提示
7:19　２問目　サムネイルの問題　西大和中　問題解説
14:59　まとめ
15:17　家庭教師のアスピレーション　生徒募集のご案内
16:23　おすすめ動画紹介（ピアノ演奏付き）

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学#西大和学園中学

指導講師：こばちゃん塾

投稿日：2022.03.07

＜関連動画＞

福田のおもしろ数学103〜麻布中学の算数〜二つの三角形の面積の差

単元： #算数(中学受験)#平面図形#角度と面積

指導講師：福田次郎

問題文全文(内容文)：
AB=5, BC=BD=6のとき、$\triangle$ABEと$\triangle$CDEの面積の差を求めよ。(※動画参照)

この動画を見る　

【小６　算数】　　小６－３１　　比例の利用

単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
①同じチョコを6個買ったら150円でした。
このチョコを24個買うといくら？
※表は動画内参照

②同じ大きさのペン25本の重さは160g。
このペン200本の重さは何g？

③同じ種類のくぎ12本の重さは48g。
何本のくぎを集めると240gになるかな？

④同じ種類の画用紙12枚の重さは60g。
この画用紙90枚の重さは何g？

この動画を見る　

【中学受験問題に挑戦】71（”大人”は頭の体操）正六角形を並べた

単元： #算数(中学受験)#平面図形#平面図形その他

指導講師：算数・数学ちゃんねる

問題文全文(内容文)：
まわりの辺の数は?
※正六角形を左の図のように20段目まで並べる
※図は動画内参照

この動画を見る　

【算数】小4-41 面積の求め方のくふう

単元： #算数(中学受験)#平面図形#角度と面積

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
算数　小4　面積の求め方のくふう
以下の図形の面積を求めよ。
＜①～⑤図形＞
①＿＿＿㎠、②＿＿＿㎠、③＿＿＿㎠、④＿＿＿㎠、⑤＿＿＿㎠
※図は動画内参照

この動画を見る　

福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面

単元： #算数(中学受験)#立体図形#立体切断

指導講師：福田次郎

問題文全文(内容文)：
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①～⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)

この動画を見る　

＜関連動画＞

福田のおもしろ数学103〜麻布中学の算数〜二つの三角形の面積の差

【小６ 算数】 小６－３１ 比例の利用

【中学受験問題に挑戦】71（”大人”は頭の体操）正六角形を並べた

【算数】小4-41 面積の求め方のくふう

福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面

【小６　算数】　　小６－３１　　比例の利用