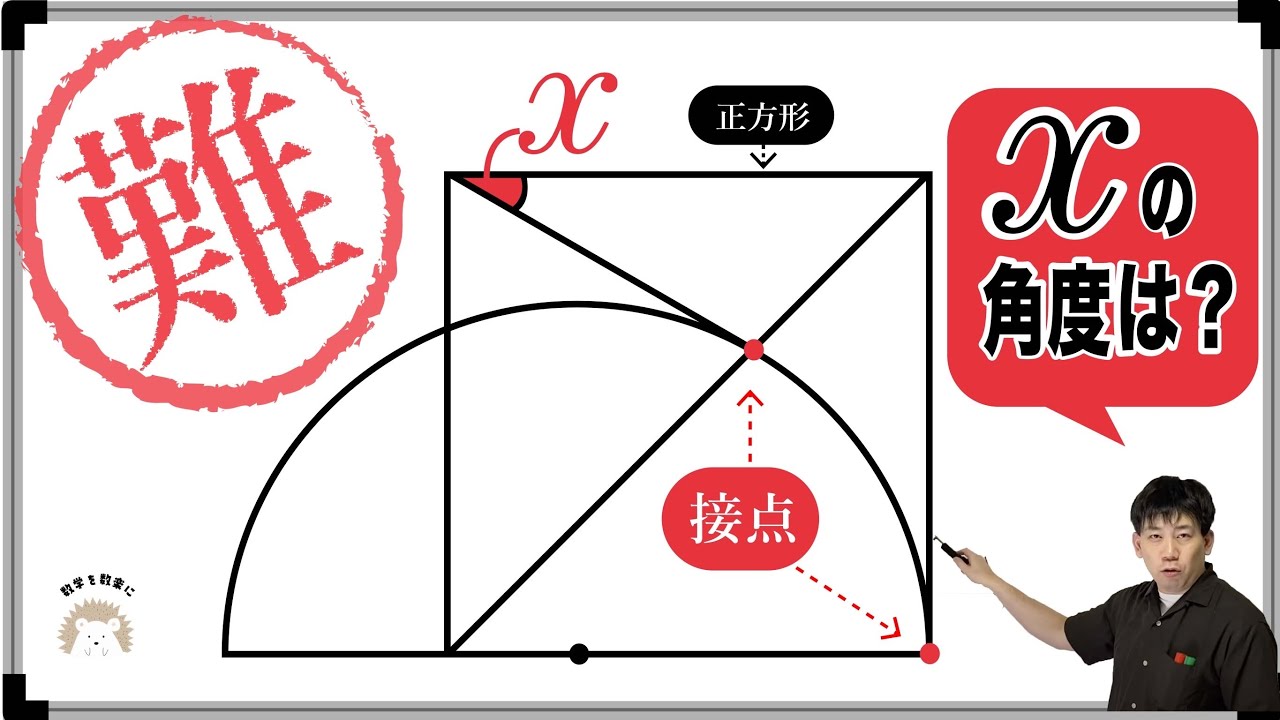
問題文全文(内容文):
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
高校受験対策・図形28
Q
図1のように、円$o$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、 $△ABC$をつくる。
点$C$をふくまない$\stackrel{\huge\frown}{AB}$上に、点$D$を$\angle DAB \lt \angle BAC$となるようにとり、点$B$と点$D$を線分で結ぶ。
線分$CD$上に点$E$を$∠EAC=∠DAB$となるようにとる。
①図1において、$\triangle ADE \backsim \triangle ABC$を証明しなさい。
②図2は、図1において$\angle BAC=60°$、点$C$を含まない$\stackrel{\huge\frown}{AD}$と$\stackrel{\huge\frown}{DB}$の長さの比が$3:1$となる場合を表している。
図2において、円$o$の半径が4cmのとき、$△ADC$の面積を求めなさい。
投稿日:2019.11.30