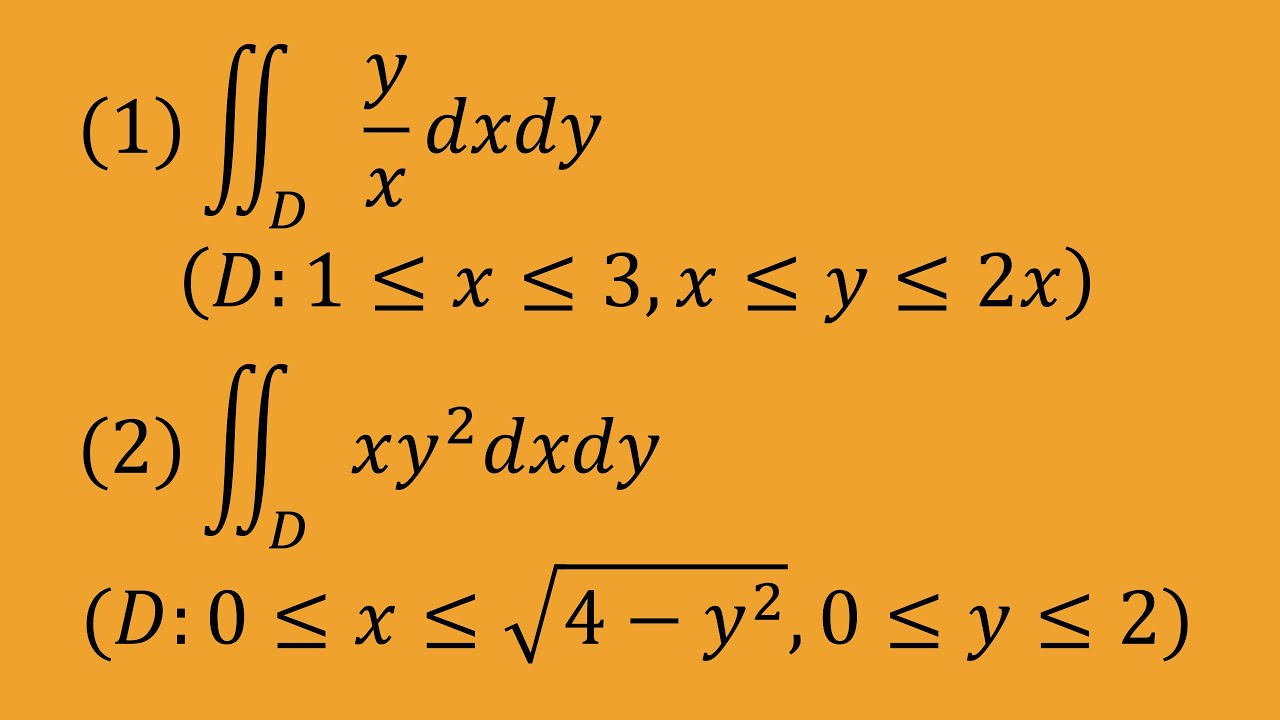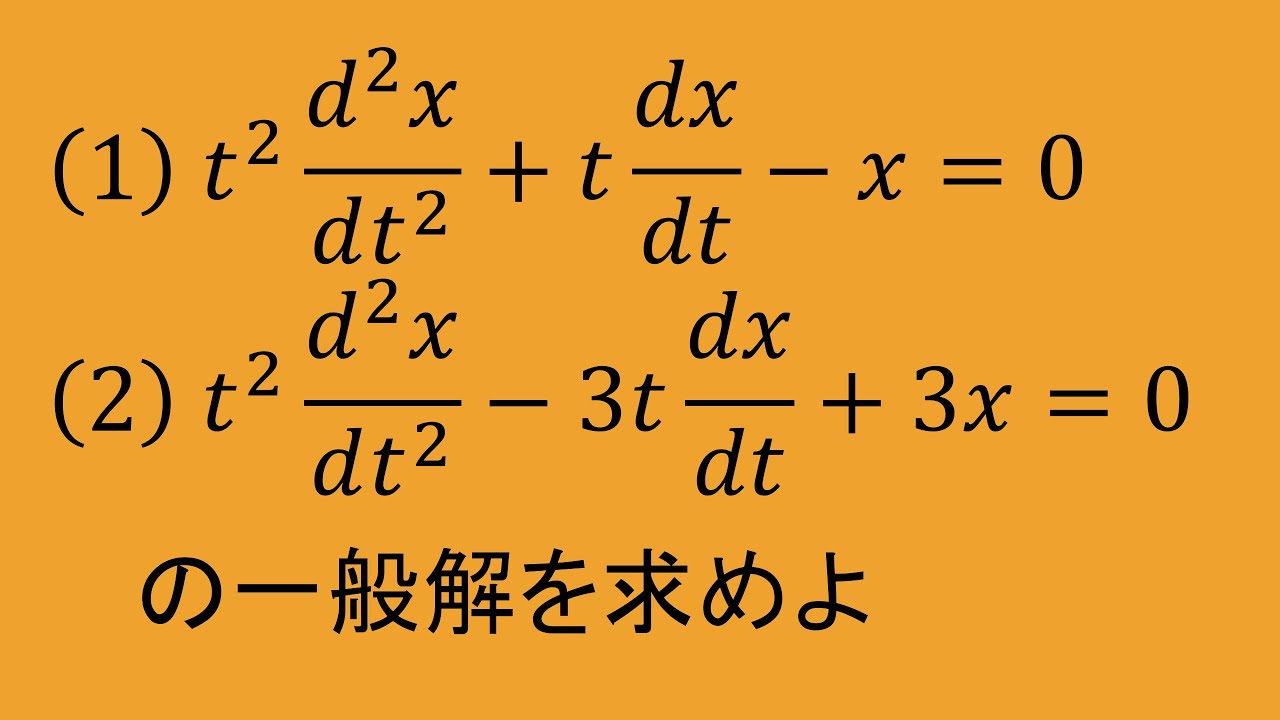数検１級ルートの中にℹ︎

問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$
外側の平方根は実部が正

単元： #数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級

指導講師：鈴木貫太郎

問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$
外側の平方根は実部が正

投稿日：2019.09.13

単元： #数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験

指導講師：ますただ

問題文全文(内容文)：
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$の
一般解を求めよ.

この動画を見る　

単元： #数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\boxed{7}$
以下を解け.

$\displaystyle \int_{0}^{3} dy \displaystyle \int_{0}^{\sqrt{\frac{y}{3}}}\ \log(x^3-3x+3)dx$

この動画を見る　

単元： #大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学検定#数学検定1級#数学(高校生)#数Ⅲ#高専(高等専門学校)

指導講師：ますただ

問題文全文(内容文)：
$∬_D(4-x^2-y^2)dxdy$
$D:x^2+(y-1)^2 \leqq 1 $ , $y \leqq x$

この動画を見る　

単元： #数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#数学検定#数学検定1級#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\dfrac{dy}{dx}=(x+y)^2$
の一般解を求めよ.

この動画を見る　

指導講師：ますただ

問題文全文(内容文)：
非同次2階微分方程式を解説していきます.

この動画を見る　