問題文全文(内容文):
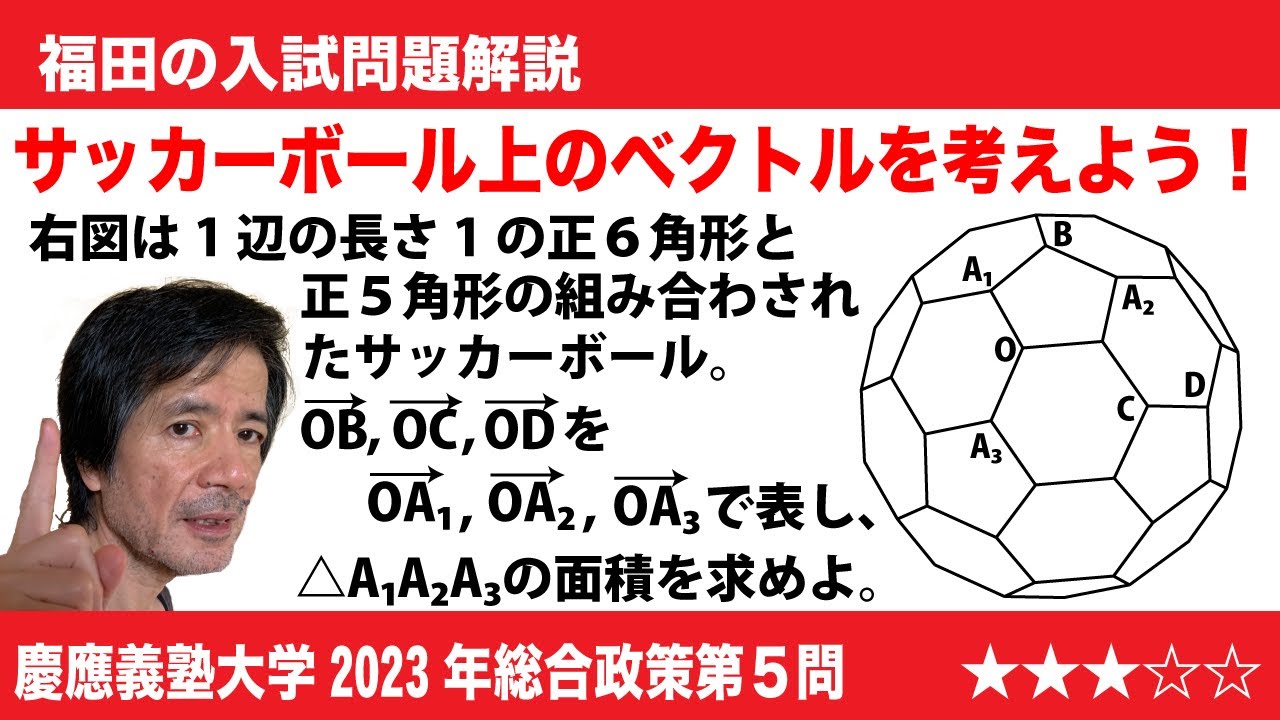
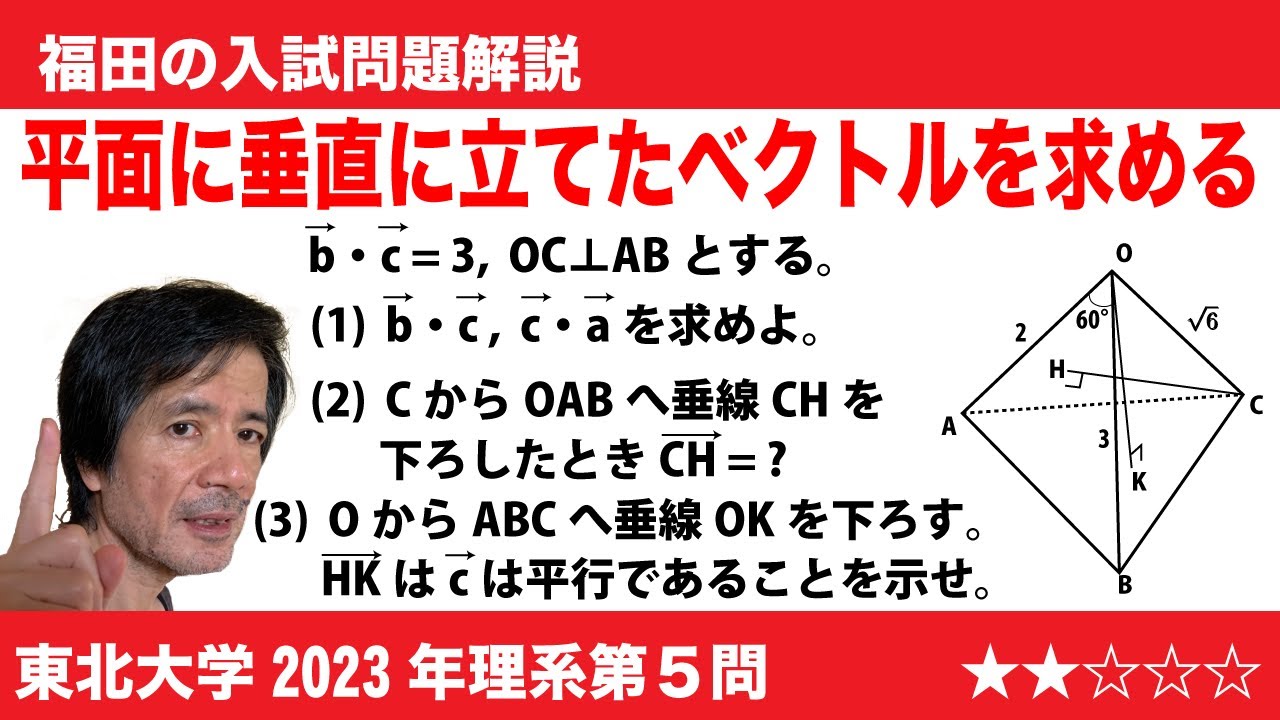
平面$\alpha$上にある長方形$\rm ABCD$と、$\alpha$上にない点$\rm O$で定まる四角錐$\rm O$-$\rm ABCD$を
考える。$\overrightarrow{\rm OA}=\vec{a},\overrightarrow{\rm OB} =\vec{b},\overrightarrow{\rm OC} =\vec{c},\overrightarrow{\rm OD} =\vec{d},$ とするとき、
$|\vec{a}|=9, |\vec{b}|=7,|\vec{c}|=2\sqrt{11},\vec{a}\cdot \vec{b}= 33,\vec{b}\cdot\vec{c} = 34$
である。
(1)$\vec{d}$を$\vec{a},\vec{b},\vec{c}$で表すと$\vec{d}=\boxed{オ}\vec{a}+\boxed{カ}\vec{b}+\boxed{キ}\vec{c}$
(2) $\vec{a}\cdot \vec{c}=\boxed{ク}$
(3) $\rm O$から平面$\alpha$に垂線$\rm OH$を下ろすと$\overrightarrow{\rm OH}=\dfrac{\boxed{ケ}}{\boxed{コ}}\vec a+\dfrac{\boxed{サ}}{\boxed{シ}}\vec b+\dfrac{\boxed{ス}}{\boxed{セ}}\vec c$であり点$\rm H$は$\boxed{う}$ にある。
(4) 長方形$\rm ABCD$の面積は$\boxed{ソ}$である。
(5) 四角錐$\rm O$-$\rm ABCD$の体積は$\boxed{タ}$である。
平面$\alpha$上にある長方形$\rm ABCD$と、$\alpha$上にない点$\rm O$で定まる四角錐$\rm O$-$\rm ABCD$を
考える。$\overrightarrow{\rm OA}=\vec{a},\overrightarrow{\rm OB} =\vec{b},\overrightarrow{\rm OC} =\vec{c},\overrightarrow{\rm OD} =\vec{d},$ とするとき、
$|\vec{a}|=9, |\vec{b}|=7,|\vec{c}|=2\sqrt{11},\vec{a}\cdot \vec{b}= 33,\vec{b}\cdot\vec{c} = 34$
である。
(1)$\vec{d}$を$\vec{a},\vec{b},\vec{c}$で表すと$\vec{d}=\boxed{オ}\vec{a}+\boxed{カ}\vec{b}+\boxed{キ}\vec{c}$
(2) $\vec{a}\cdot \vec{c}=\boxed{ク}$
(3) $\rm O$から平面$\alpha$に垂線$\rm OH$を下ろすと$\overrightarrow{\rm OH}=\dfrac{\boxed{ケ}}{\boxed{コ}}\vec a+\dfrac{\boxed{サ}}{\boxed{シ}}\vec b+\dfrac{\boxed{ス}}{\boxed{セ}}\vec c$であり点$\rm H$は$\boxed{う}$ にある。
(4) 長方形$\rm ABCD$の面積は$\boxed{ソ}$である。
(5) 四角錐$\rm O$-$\rm ABCD$の体積は$\boxed{タ}$である。
単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
平面$\alpha$上にある長方形$\rm ABCD$と、$\alpha$上にない点$\rm O$で定まる四角錐$\rm O$-$\rm ABCD$を
考える。$\overrightarrow{\rm OA}=\vec{a},\overrightarrow{\rm OB} =\vec{b},\overrightarrow{\rm OC} =\vec{c},\overrightarrow{\rm OD} =\vec{d},$ とするとき、
$|\vec{a}|=9, |\vec{b}|=7,|\vec{c}|=2\sqrt{11},\vec{a}\cdot \vec{b}= 33,\vec{b}\cdot\vec{c} = 34$
である。
(1)$\vec{d}$を$\vec{a},\vec{b},\vec{c}$で表すと$\vec{d}=\boxed{オ}\vec{a}+\boxed{カ}\vec{b}+\boxed{キ}\vec{c}$
(2) $\vec{a}\cdot \vec{c}=\boxed{ク}$
(3) $\rm O$から平面$\alpha$に垂線$\rm OH$を下ろすと$\overrightarrow{\rm OH}=\dfrac{\boxed{ケ}}{\boxed{コ}}\vec a+\dfrac{\boxed{サ}}{\boxed{シ}}\vec b+\dfrac{\boxed{ス}}{\boxed{セ}}\vec c$であり点$\rm H$は$\boxed{う}$ にある。
(4) 長方形$\rm ABCD$の面積は$\boxed{ソ}$である。
(5) 四角錐$\rm O$-$\rm ABCD$の体積は$\boxed{タ}$である。
平面$\alpha$上にある長方形$\rm ABCD$と、$\alpha$上にない点$\rm O$で定まる四角錐$\rm O$-$\rm ABCD$を
考える。$\overrightarrow{\rm OA}=\vec{a},\overrightarrow{\rm OB} =\vec{b},\overrightarrow{\rm OC} =\vec{c},\overrightarrow{\rm OD} =\vec{d},$ とするとき、
$|\vec{a}|=9, |\vec{b}|=7,|\vec{c}|=2\sqrt{11},\vec{a}\cdot \vec{b}= 33,\vec{b}\cdot\vec{c} = 34$
である。
(1)$\vec{d}$を$\vec{a},\vec{b},\vec{c}$で表すと$\vec{d}=\boxed{オ}\vec{a}+\boxed{カ}\vec{b}+\boxed{キ}\vec{c}$
(2) $\vec{a}\cdot \vec{c}=\boxed{ク}$
(3) $\rm O$から平面$\alpha$に垂線$\rm OH$を下ろすと$\overrightarrow{\rm OH}=\dfrac{\boxed{ケ}}{\boxed{コ}}\vec a+\dfrac{\boxed{サ}}{\boxed{シ}}\vec b+\dfrac{\boxed{ス}}{\boxed{セ}}\vec c$であり点$\rm H$は$\boxed{う}$ にある。
(4) 長方形$\rm ABCD$の面積は$\boxed{ソ}$である。
(5) 四角錐$\rm O$-$\rm ABCD$の体積は$\boxed{タ}$である。
投稿日:2024.09.26