これは知らなきゃ損 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 計算と数の性質 > いろいろな計算 > これは知らなきゃ損

これは知らなきゃ損

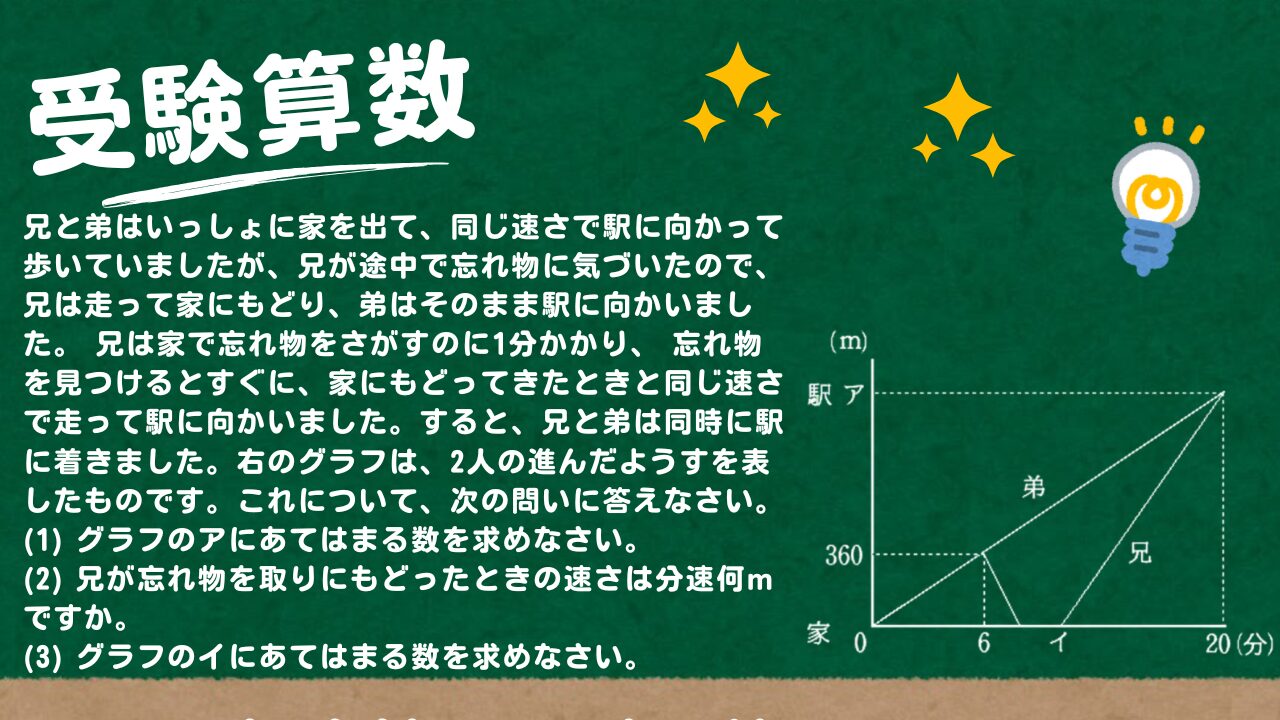
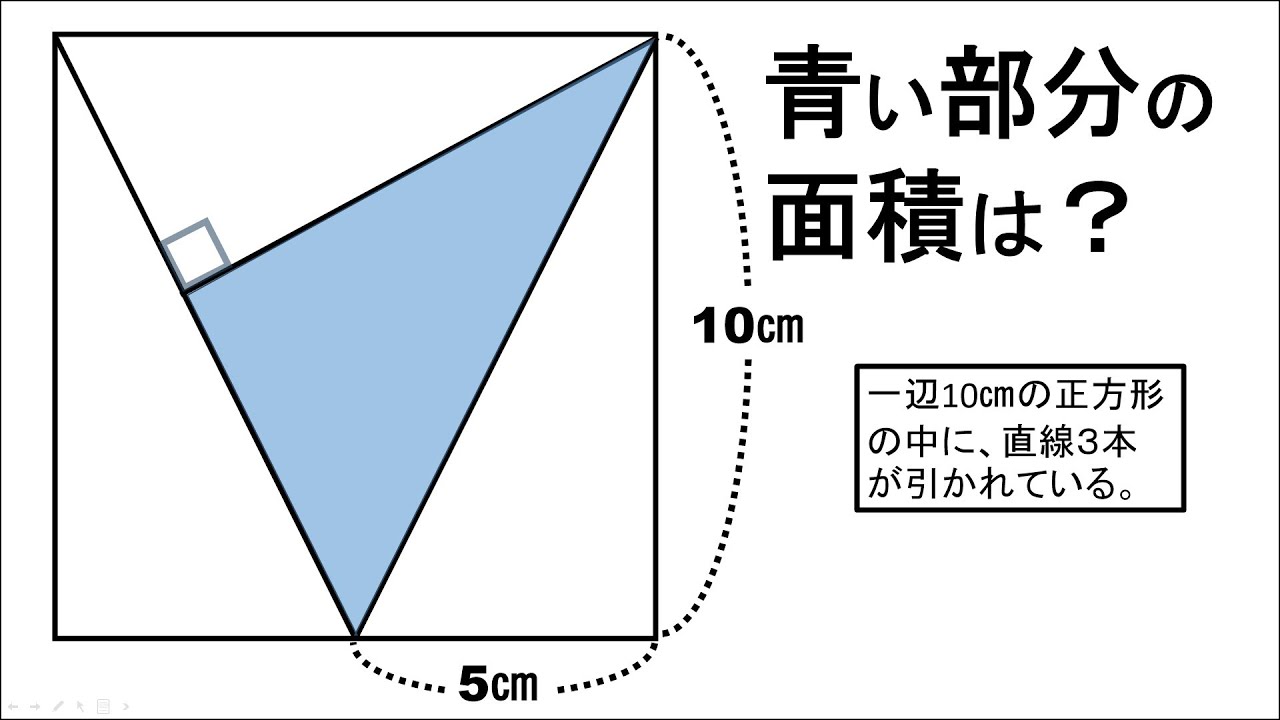
問題文全文(内容文)：
分数の足し算引き算の便利な解き方紹介動画です
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
分数の足し算引き算の便利な解き方紹介動画です
投稿日：2022.03.13

＜関連動画＞

【算数パズル】気づけば一瞬！「角ADEの大きさは？？」

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積#図形の移動
指導講師： いつもの先生
問題文全文(内容文)：
角ADEの大きさは？

＊図は動画内参照
この動画を見る　

ある事実に気づけば一瞬！正十角形と正方形の性質を上手く使う良問！【中学受験算数】【入試問題】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#角度と面積
指導講師： こばちゃん塾
問題文全文(内容文)：
2023豊島岡女子学園中学校
下図のように正十角形ABCDEFGHIJがあり、ACを1辺とする正方形ACPQを正十角形の内側につくります。このとき、角CPEの大きさは何度？
＊図は動画内参照
この動画を見る　

【受験対策】　　数学－規則性③

アイキャッチ画像
単元： #算数(中学受験)#その他
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、奇数のカードを1，3，5…という
順番で、1段目が1枚、2段目が2枚、3段目が3枚、…と上から規則的に並べていきます。

①1段目から5段目までのカードに書かれた数の和は？

②6段目の右端に並ぶカードに書かれた数は？

③17段目の右端に並ぶカードの左隣にあるカードに書かれた数は？
※図は動画内参照
この動画を見る　

高評価か？低評価か？

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算
指導講師： 数学を数楽に
問題文全文(内容文)：
$1 \div (\frac{1}{3})^3 =$
この動画を見る　

【解けなきゃ小学生以下！？】工夫次第で鮮やかに解ける面積パズル５選！

アイキャッチ画像
単元： #算数(中学受験)#平面図形#平面図形その他
指導講師： こばちゃん塾
問題文全文(内容文)：
初級①
xの面積=?
中級①
xの面積=?
中級②
xの面積=?
上級①
xの面積=?
上級②
xの面積=?

＊図は動画内参照
この動画を見る　
トップへ戻る