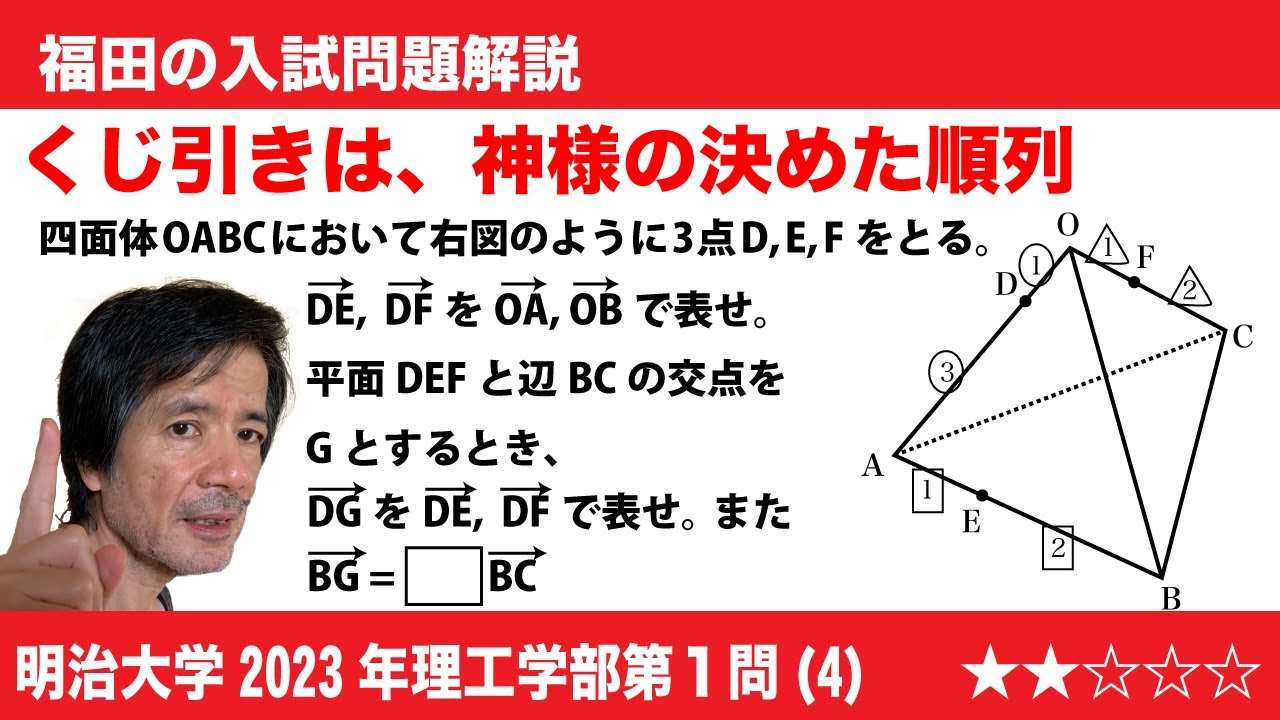
問題文全文(内容文):
球面の方程式の解釈と求め方について解説します。
球面の方程式の解釈と求め方について解説します。
単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
3rd School
問題文全文(内容文):
球面の方程式の解釈と求め方について解説します。
球面の方程式の解釈と求め方について解説します。
投稿日:2022.05.18