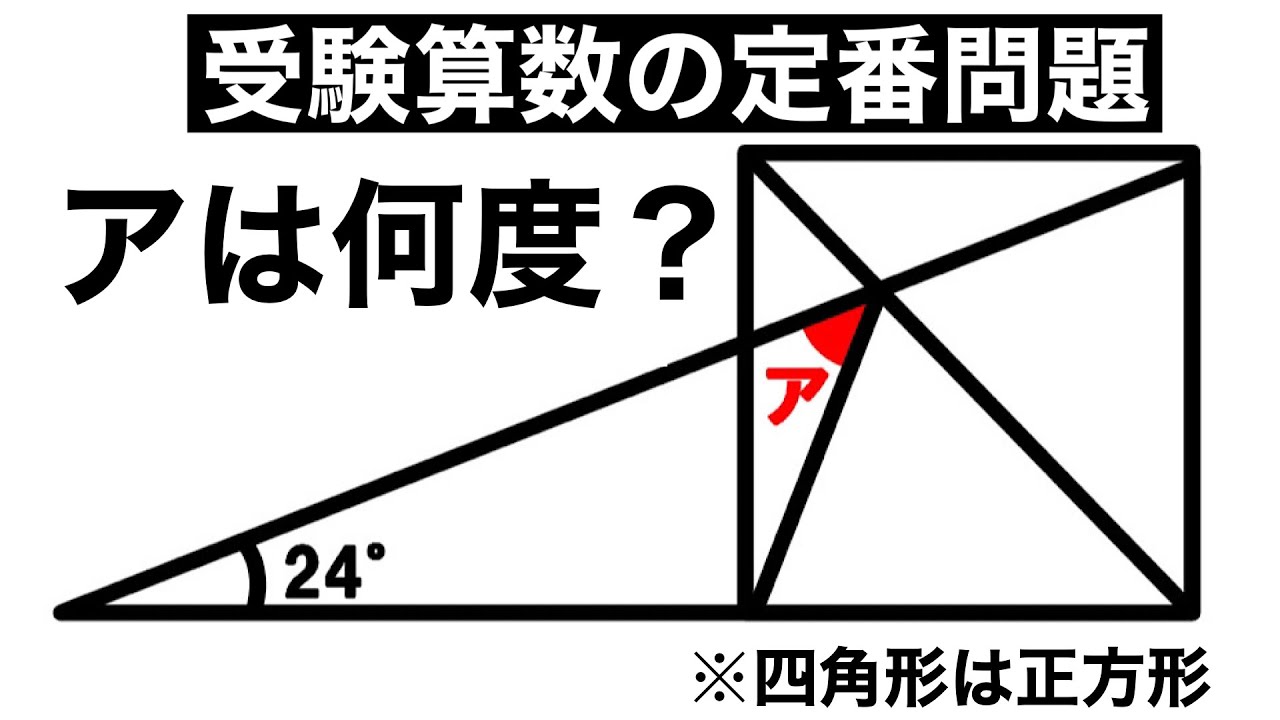
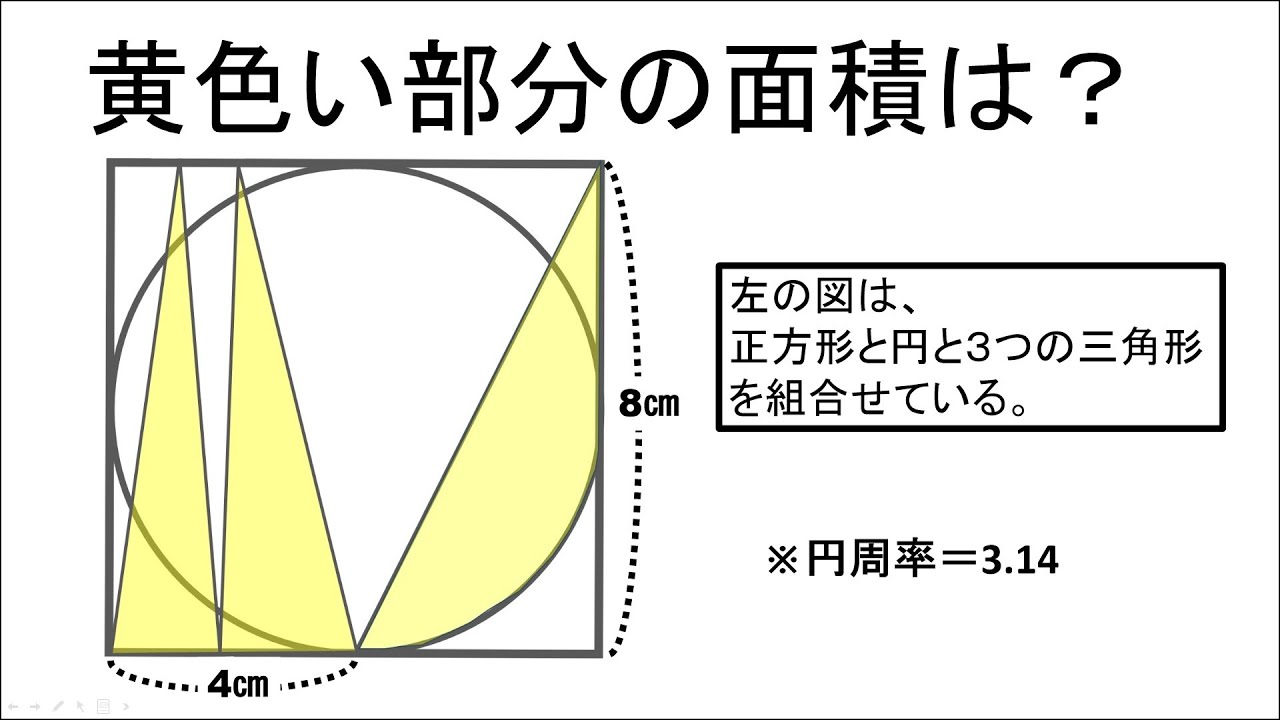
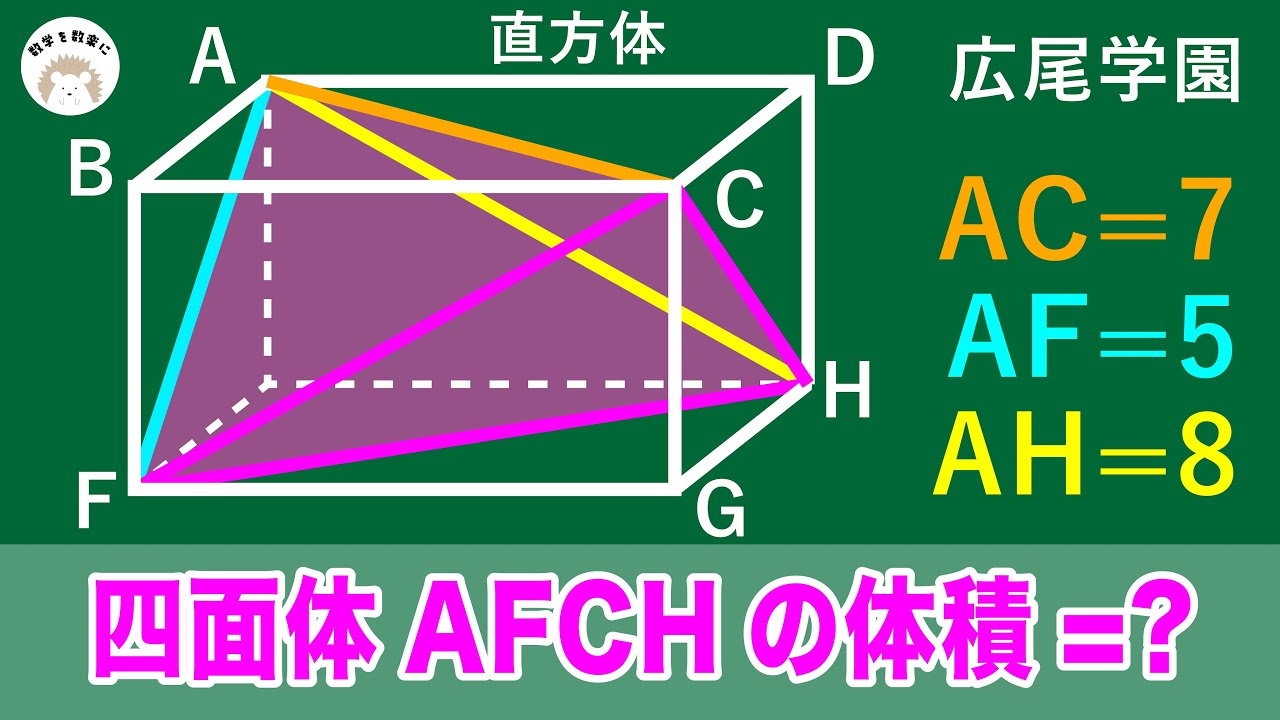
問題文全文(内容文):
ある中学校の生徒数を調べたところ、1年生は全体の36%で、2年生は全体の28%よりも10人多く、3年生は全体の1/3よりも4人少ないことがわかりました。これについて、次の問いに答えなさい。
(1)生徒数は3学年合わせて何人ですか。
(2)2年生と3年生の生徒数の差は何人ですか。
ある中学校の生徒数を調べたところ、1年生は全体の36%で、2年生は全体の28%よりも10人多く、3年生は全体の1/3よりも4人少ないことがわかりました。これについて、次の問いに答えなさい。
(1)生徒数は3学年合わせて何人ですか。
(2)2年生と3年生の生徒数の差は何人ですか。
チャプター:
0:00 オープニング・問題文
0:15 (1)解説
2:30 (2)解説
単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある中学校の生徒数を調べたところ、1年生は全体の36%で、2年生は全体の28%よりも10人多く、3年生は全体の1/3よりも4人少ないことがわかりました。これについて、次の問いに答えなさい。
(1)生徒数は3学年合わせて何人ですか。
(2)2年生と3年生の生徒数の差は何人ですか。
ある中学校の生徒数を調べたところ、1年生は全体の36%で、2年生は全体の28%よりも10人多く、3年生は全体の1/3よりも4人少ないことがわかりました。これについて、次の問いに答えなさい。
(1)生徒数は3学年合わせて何人ですか。
(2)2年生と3年生の生徒数の差は何人ですか。
投稿日:2025.10.06