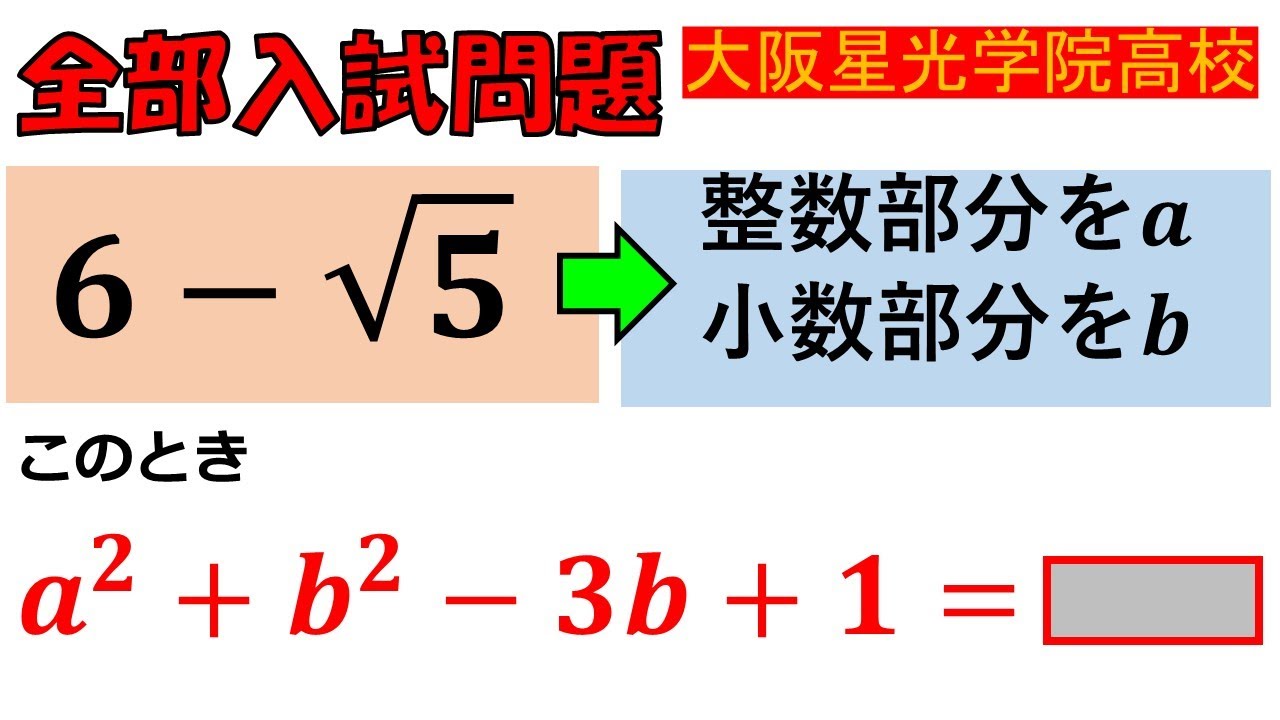
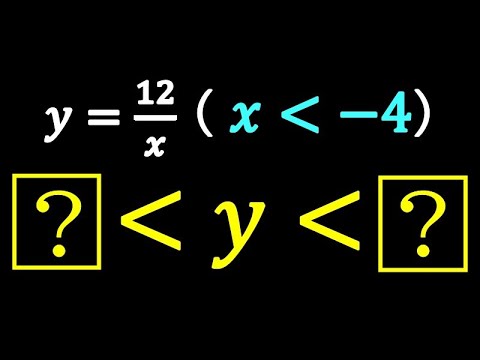問題文全文(内容文):
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
中1~第24回規則性と文字式~
例題
「規則の問題はほとんど、 次の図のように棒を並べて正三角形を次々と作っていきます。
(1)正三角形を5個作るとき、棒は何本使いますか。
(2)正三角形をn個作るとき、棒は何本使いますか。
投稿日:2020.10.16