【受験算数】数の性質：東京都市大学付属(2020年度)第1回大問1-1 次の計算をしよう。1/15+1/24+1/35+1/48+1/63

【受験算数】数の性質：東京都市大学付属(2020年度)第1回大問1-1　次の計算をしよう。1/15+1/24+1/35+1/48+1/63

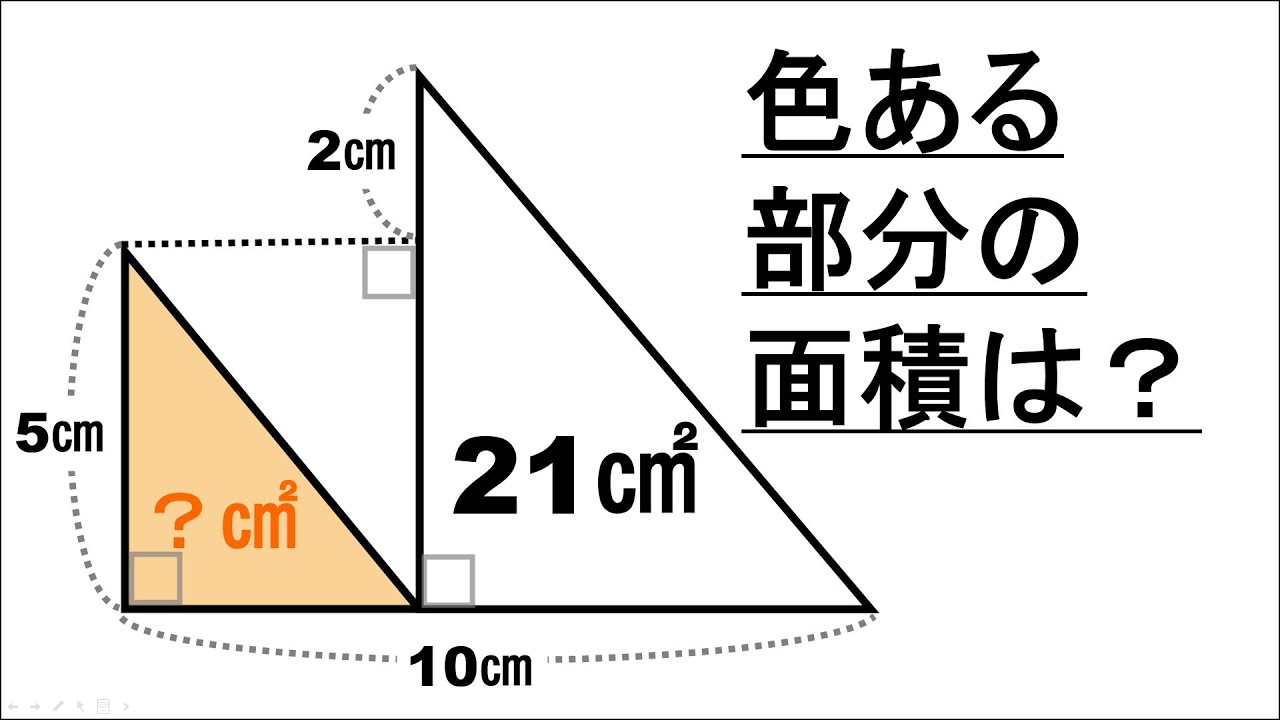
問題文全文(内容文)：
次の計算をしよう。

\frac{1}{15} + \frac{1}{24} + \frac{1}{35} + \frac{1}{48} + \frac{1}{63}

チャプター：

0:00 オープニング
0:05 問題文
0:11 問題解説
2:17 名言

単元： #算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#東京都市大学付属中学

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の計算をしよう。

\frac{1}{15} + \frac{1}{24} + \frac{1}{35} + \frac{1}{48} + \frac{1}{63}

投稿日：2021.02.08

＜関連動画＞

【中学受験問題に挑戦】97　（”大人”は頭の体操）　三角形の中におうぎ形（面積問題）

単元： #算数(中学受験)#平面図形

指導講師：算数・数学ちゃんねる

問題文全文(内容文)：
緑色の部分の面積を求めよ。
三角形とおうぎ形2つを組み合わせ、
AM=BMは対等です。

※上記は辺の長さの関係です。
※円周率=3.14

※図は動画内参照

この動画を見る　

【小6算数手元解説】得票数（応用）途中開票【問題文は概要欄】

単元： #算数(中学受験)#場合の数#場合の数

指導講師：理数個別チャンネル

問題文全文(内容文)：
120人が投票して４人の委員を選ぶ選挙をします。A、B、C、D、E、Fの6人が立候補しました。得票の上位4人を当選とします。次の問に答えなさい。

１）A君が他の5人の得票と関係なく当選するには、最低何票あればよいでしょうか。

２）開票の途中でA君は19票、B君は28票、C君は18票、D君は11票、E君は15票、F君は12票になりました。A君はあと何票あれば当選となりますか。

この動画を見る　

2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

単元： #算数(中学受験)#文章題#売買損益と食塩水

指導講師：重吉

問題文全文(内容文)：
容器

A

には6%の食塩水が300g,容器

B

には12%の食塩水が500g入っています.
両方の容器から同じ量の食塩水を同時に取り出し,それぞれもう一方の容器に入れたところ,

A

に入っている食塩水の濃さは10%になりました.

B

に入っている食塩水の濃さは

になります.

を求めよ.

2024年明治大付属明治中過去問

この動画を見る　

マリオがブロックを破壊するすごさ計算してみた...

単元： #算数(中学受験)#立体図形#立体図形その他#理科(中学生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
マリオがブロックを破壊するすごさ計算してみた...

この動画を見る　

上底・下底・高さ、全てが分からない台形の面積って求められるの？⇒はい、可能です！【中学受験算数】【慶應義塾普通部】

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾普通部

指導講師：こばちゃん塾

問題文全文(内容文)：
・下図の四角形ABCDは正方形で曲線は円の一部です。
このとき、おうぎ形ABDの周の長さは？

・右下の図で、3つの正方形はすべて同じ大きさです。また、ADとBCは平行です。
このとき、台形ABCDの面積は？

＊図は動画内参照

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【受験算数】数の性質：東京都市大学付属(2020年度)第1回 大問1-1 次の計算をしよう。1/15+1/24+1/35+1/48+1/63

＜関連動画＞

【中学受験問題に挑戦】97 （”大人”は頭の体操） 三角形の中におうぎ形（面積問題）

【小6算数手元解説】得票数（応用）途中開票【問題文は概要欄】

2024年明治大付属明治中算数「食塩水濃度」中学受験指導歴20年以上のプロ解説

マリオがブロックを破壊するすごさ計算してみた...

上底・下底・高さ、全てが分からない台形の面積って求められるの？⇒はい、可能です！【中学受験算数】【慶應義塾普通部】

【受験算数】数の性質：東京都市大学付属(2020年度)第1回大問1-1　次の計算をしよう。1/15+1/24+1/35+1/48+1/63

【中学受験問題に挑戦】97　（”大人”は頭の体操）　三角形の中におうぎ形（面積問題）