問題文全文(内容文):
問2
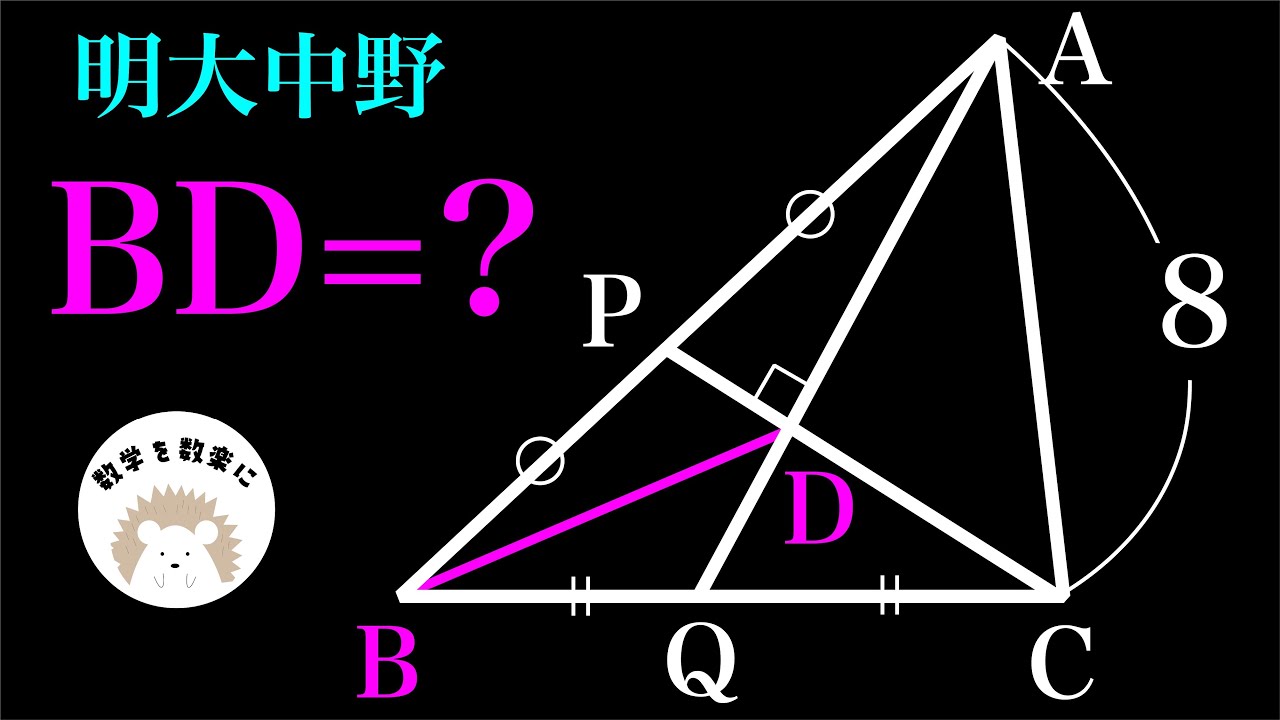
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
単元:
#数学(中学生)#中1数学#中3数学#空間図形#三平方の定理
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
問2
右の図の正四面体は、1辺の長さが8cmである。辺$BC$、$CD$の中点をそれぞれ点$P$、Q、 点$Q$から$AP$にひいた垂線と$AP$との交点を$R$とする。次の(1)~(4)に答えなさい。
(1) $AQ$の長さを求めなさい。
(2) $△APQ$の面積を求めなさい。
(3) $QR$の長さを求めなさい。
(4) 三角すい$RBCD$の体積は、正四面体$ABCD$の体積の何倍か、求めなさい
投稿日:2019.01.19