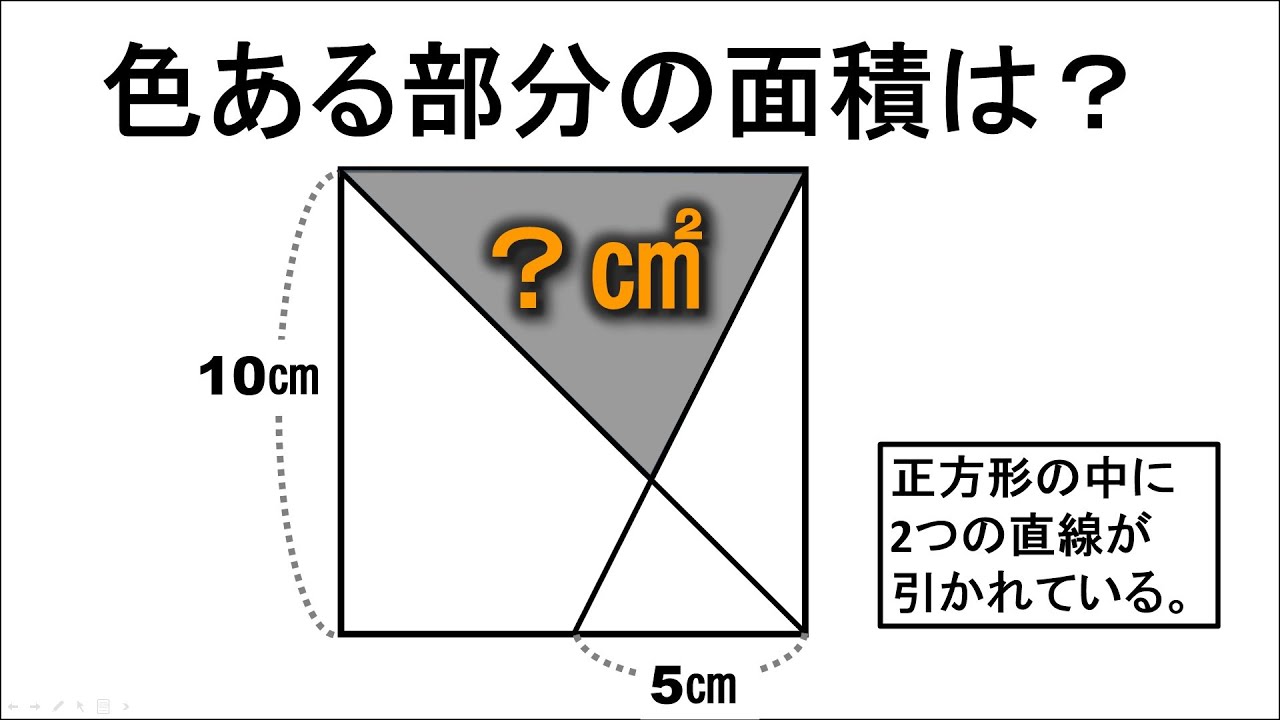
問題文全文(内容文):
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
チャプター:
00:00 スタート
00:10 (1)解説
03:54 (2)解説
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
投稿日:2025.07.11