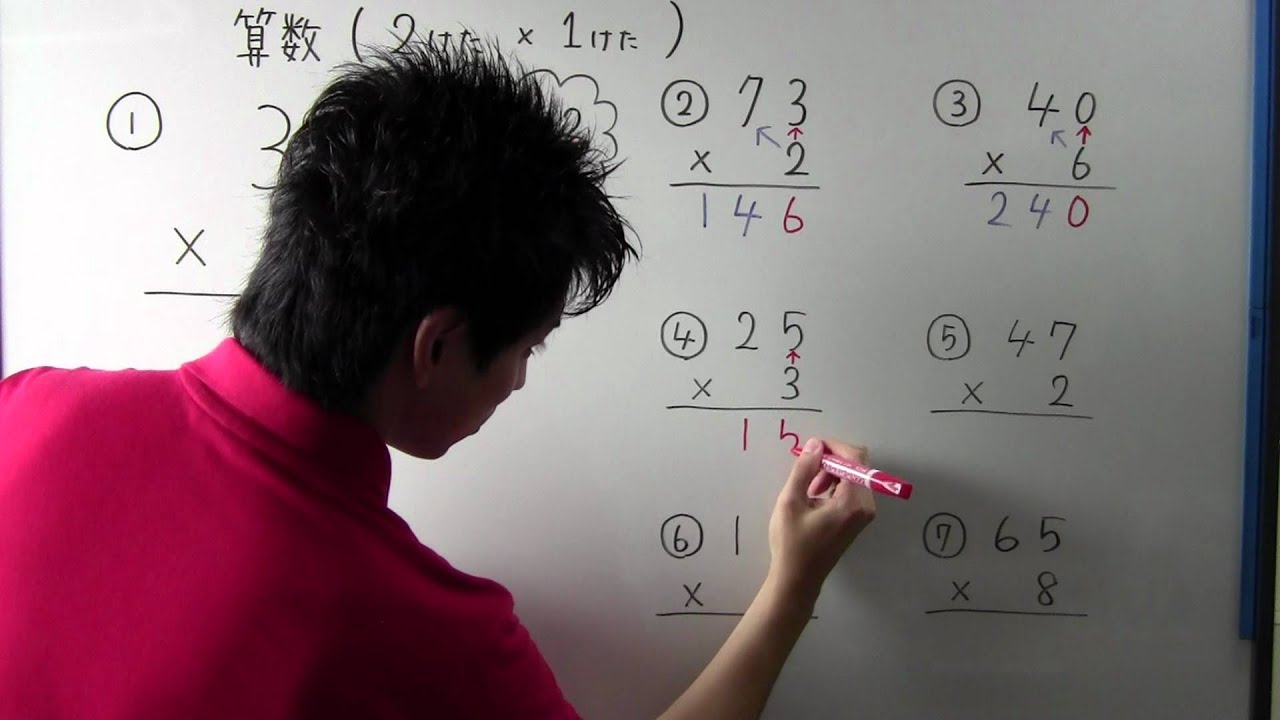【小４ 算数】 小４－３３ 計算のくふう③ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 計算と数の性質 > いろいろな計算 > 【小４　算数】　　小４－３３　　計算のくふう③

【小４　算数】　　小４－３３　　計算のくふう③

問題文全文(内容文)：
小４　算数　計算のくふう③
以下の問に答えよ
Q　$8\times4=32$ をもとにすると
① $8\times40=$
② $80\times4=$
③ $80\times40=$
④ $8\times400=$
Q　$17\times3=51$ をもとにすると
⑤ $17\times30=$
⑥ $1700\times3=$
⑦ $170\times300=$
⑧ $17000\times3000=$
※図は動画内参照
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
小４　算数　計算のくふう③
以下の問に答えよ
Q　$8\times4=32$ をもとにすると
① $8\times40=$
② $80\times4=$
③ $80\times40=$
④ $8\times400=$
Q　$17\times3=51$ をもとにすると
⑤ $17\times30=$
⑥ $1700\times3=$
⑦ $170\times300=$
⑧ $17000\times3000=$
※図は動画内参照
投稿日：2012.10.22

＜関連動画＞

大人には難しすぎる！？超面白い工夫ができる一題！【中学受験算数】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師： こばちゃん塾
問題文全文(内容文)：
左図でEBの長さは？
＊図は動画内参照
この動画を見る　

1+1=1になります。なぜ？

アイキャッチ画像
単元： #その他
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
1+1=1になる理由解説
この動画を見る　

換気せんの面積　　名古屋高校

アイキャッチ画像
単元： #数学(中学生)#中１数学#中３数学#円#平面図形#角度と面積#平面図形#高校入試過去問(数学)
指導講師： 数学を数楽に
問題文全文(内容文)：
斜線部の面積=?
＊図は動画内参照

名古屋高等学校
この動画を見る　

この計算方法知ってた？

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
この計算方法知ってた？
※問題文は動画内参照
この動画を見る　

中学受験算数「地図と縮尺①（長さ）」小学４年生～６年生対象【毎日配信】

アイキャッチ画像
単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第83回地図と縮尺①(長さ)

例1 実際には1kmの距離を、縮尺1/50000の地図上で表すと、 何cmになりますか。

例2 縮尺 1/2000の地図上で10cmで表されている距離は、 実際には何mありますか。

例3 実際には100mの距離を4cmで表されている地図の縮尺を、 分数で求めなさい。
この動画を見る　
PAGE TOP