問題文全文(内容文):
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
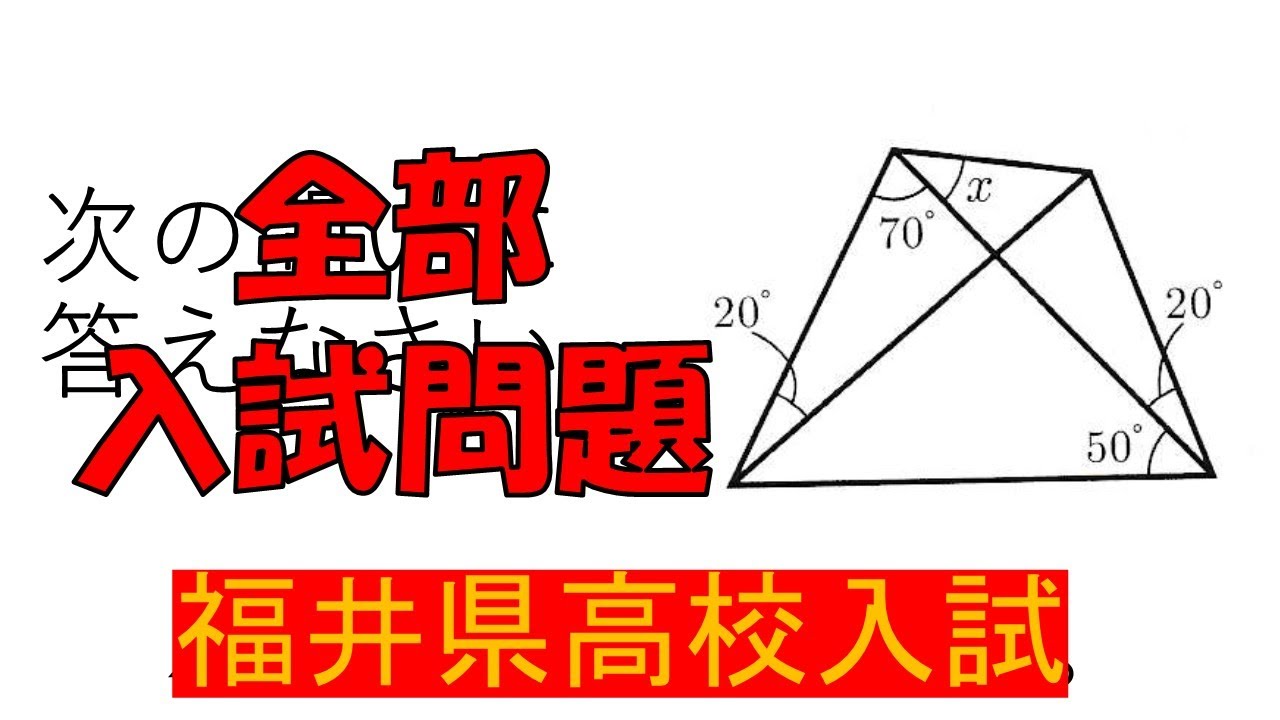
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#空間図形#1次関数#2次関数#円#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
$ \boxed{1}$
(1)$ 9xy^2\div \left(-\dfrac{3}{2}xy\right)^3\times \dfrac{3}{4}x^4y$を計算せよ.
(2)$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{4}x+\dfrac{y}{2}=1 \\
2x-3y=1
\end{array}
\right.
\end{eqnarray}$ を解け.
(3)図の円$ O $において,$ \angle x $の大きさを求めよ.
$ \boxed{2}$
放物線$ y=x^2 $上に5点$ A,B,C,D,E $があり,それぞれのx座標は,$ a,-5,-2,2,4 $である.(ただし,$ a\lt -5 $)
さらに,線分$ CE $の中点$ F $は直線$ AD $上にあるとき,あとの問いに答えよ.
(1)点$ F $の座標を求めよ.
(2)$ a $の値を求めよ.
(3)$ \triangle ABD $と$ \triangle AED $の面積の比の最も簡単な整数の比で表せ.
$ \boxed{3}$
図のように,直方体$ ABCD-EFGH $があり,$ AB=3,AD=6,AE=2$である.
点$G$からこの直方体の対角線$CE$に垂線を引き,その交点を$P$とする.
このとき,次の各問いに答えよ.
(1)線分$ GP $の長さを求めよ.
(2)三角錐$ P-GEF$の体積を求めよ.
(3)辺$ AD $の中点を$Q$とし,辺$FG$上に$FR=2$となる点$R$をとる.
3点$B,Q,R $を通る平面と線分$EG$の交点を$S$とするとき,三角錐$P-GSR $の体積を求めよ.
投稿日:2023.02.02