問題文全文(内容文):
小6 算数 反比例の式
以下の問に答えよ
[ポイント] $y$ が $x$ に反比例するとき $y =$ 決まった数 $\div x$ ( $y$ ①__ $x$ で計算)
◎面積が決まっている平行四辺形について。
<表:底辺の長さ $x$ と たかさ $y$ >
② $x$と $y$ の関係を式にすると?
③ $x$ の値が $10$ のとき、$y$ はいくつ?
④ $y$ の値が $7.5$ のとき、$x$ はいくつ?
◎ 48 L あるジュースをみんなで分けます。
<人数 $x$ (人)と、1 人分の量 $y$ (L) の表>
⑤ $x$ と $y$ の関係を式にすると?
◎反比例するのはどれ?
[ア] 100 このアメを等分するときの人数( $x$ 人)と、1 人分の個数( $y$ こ)
[イ] 1 m が 15 g の針金の長さ( $x$ m)と その重さ( $y$ g)
[ウ] 面積が 20 ㎠ の長方形のたて( $x$ cm)と横( $y$ cm)
→ ⑧___
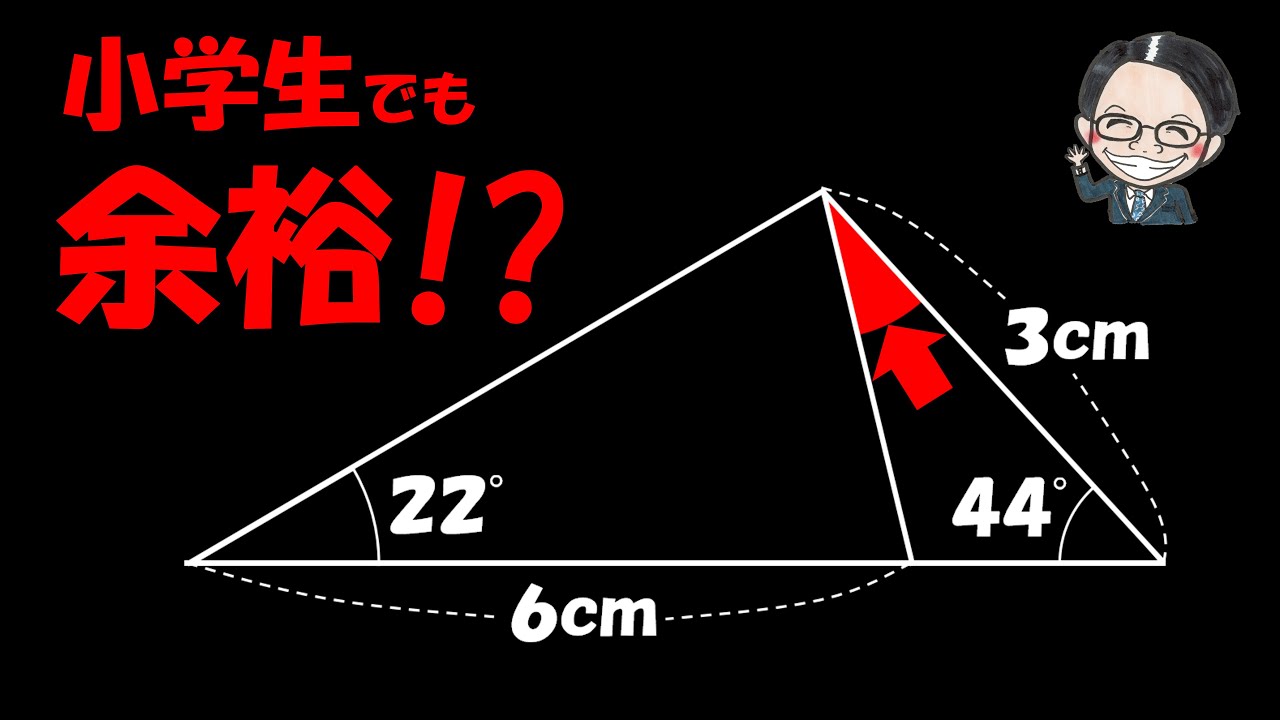
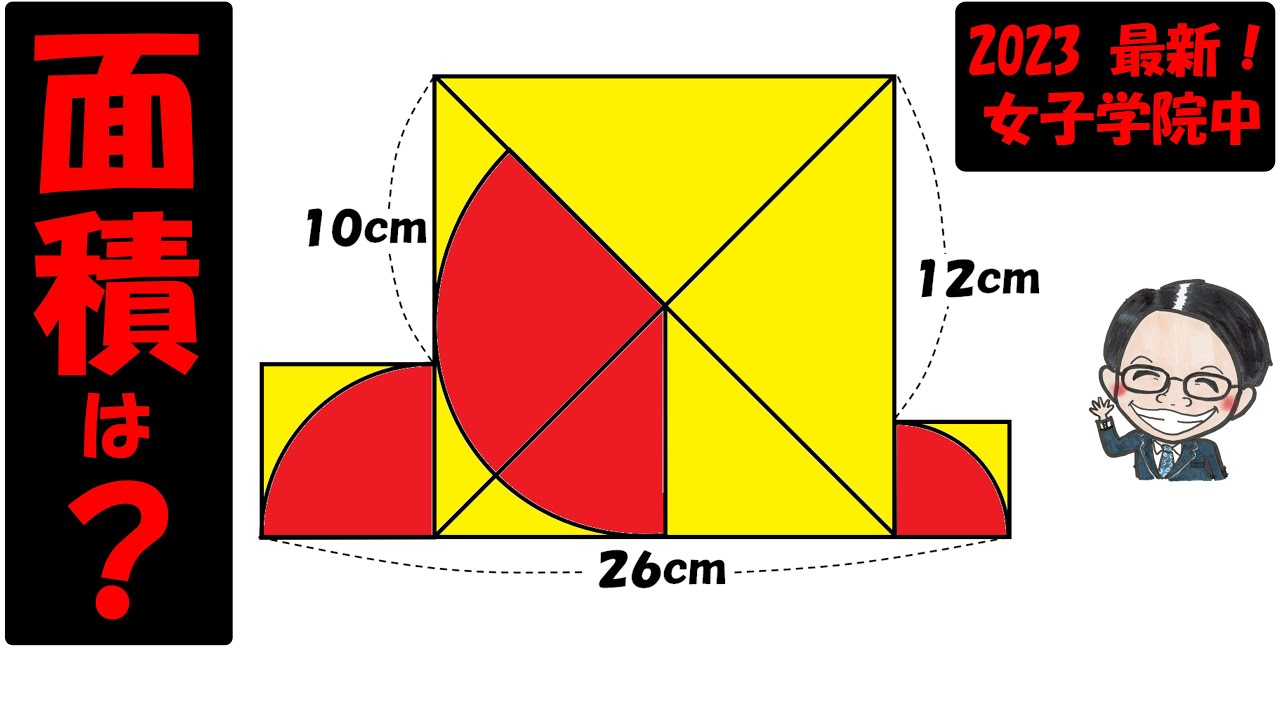
※図は動画内参照
小6 算数 反比例の式
以下の問に答えよ
[ポイント] $y$ が $x$ に反比例するとき $y =$ 決まった数 $\div x$ ( $y$ ①__ $x$ で計算)
◎面積が決まっている平行四辺形について。
<表:底辺の長さ $x$ と たかさ $y$ >
② $x$と $y$ の関係を式にすると?
③ $x$ の値が $10$ のとき、$y$ はいくつ?
④ $y$ の値が $7.5$ のとき、$x$ はいくつ?
◎ 48 L あるジュースをみんなで分けます。
<人数 $x$ (人)と、1 人分の量 $y$ (L) の表>
⑤ $x$ と $y$ の関係を式にすると?
◎反比例するのはどれ?
[ア] 100 このアメを等分するときの人数( $x$ 人)と、1 人分の個数( $y$ こ)
[イ] 1 m が 15 g の針金の長さ( $x$ m)と その重さ( $y$ g)
[ウ] 面積が 20 ㎠ の長方形のたて( $x$ cm)と横( $y$ cm)
→ ⑧___
※図は動画内参照
単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
小6 算数 反比例の式
以下の問に答えよ
[ポイント] $y$ が $x$ に反比例するとき $y =$ 決まった数 $\div x$ ( $y$ ①__ $x$ で計算)
◎面積が決まっている平行四辺形について。
<表:底辺の長さ $x$ と たかさ $y$ >
② $x$と $y$ の関係を式にすると?
③ $x$ の値が $10$ のとき、$y$ はいくつ?
④ $y$ の値が $7.5$ のとき、$x$ はいくつ?
◎ 48 L あるジュースをみんなで分けます。
<人数 $x$ (人)と、1 人分の量 $y$ (L) の表>
⑤ $x$ と $y$ の関係を式にすると?
◎反比例するのはどれ?
[ア] 100 このアメを等分するときの人数( $x$ 人)と、1 人分の個数( $y$ こ)
[イ] 1 m が 15 g の針金の長さ( $x$ m)と その重さ( $y$ g)
[ウ] 面積が 20 ㎠ の長方形のたて( $x$ cm)と横( $y$ cm)
→ ⑧___
※図は動画内参照
小6 算数 反比例の式
以下の問に答えよ
[ポイント] $y$ が $x$ に反比例するとき $y =$ 決まった数 $\div x$ ( $y$ ①__ $x$ で計算)
◎面積が決まっている平行四辺形について。
<表:底辺の長さ $x$ と たかさ $y$ >
② $x$と $y$ の関係を式にすると?
③ $x$ の値が $10$ のとき、$y$ はいくつ?
④ $y$ の値が $7.5$ のとき、$x$ はいくつ?
◎ 48 L あるジュースをみんなで分けます。
<人数 $x$ (人)と、1 人分の量 $y$ (L) の表>
⑤ $x$ と $y$ の関係を式にすると?
◎反比例するのはどれ?
[ア] 100 このアメを等分するときの人数( $x$ 人)と、1 人分の個数( $y$ こ)
[イ] 1 m が 15 g の針金の長さ( $x$ m)と その重さ( $y$ g)
[ウ] 面積が 20 ㎠ の長方形のたて( $x$ cm)と横( $y$ cm)
→ ⑧___
※図は動画内参照
投稿日:2012.11.07