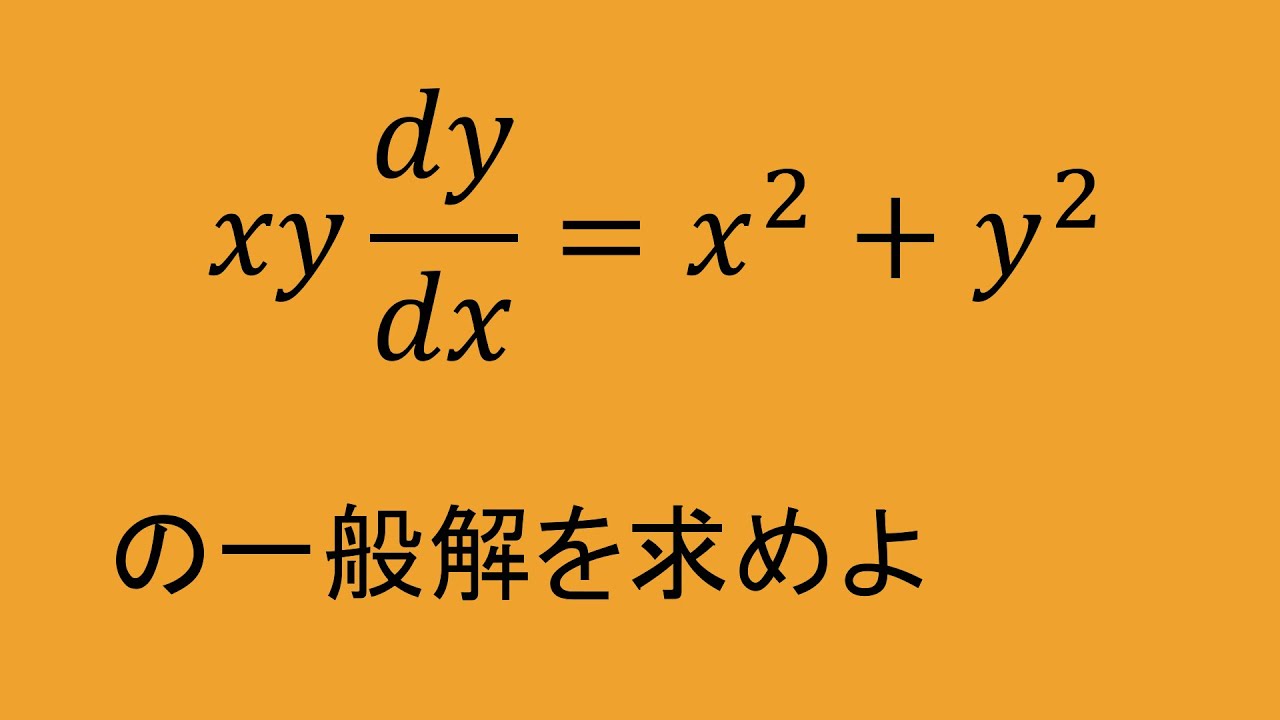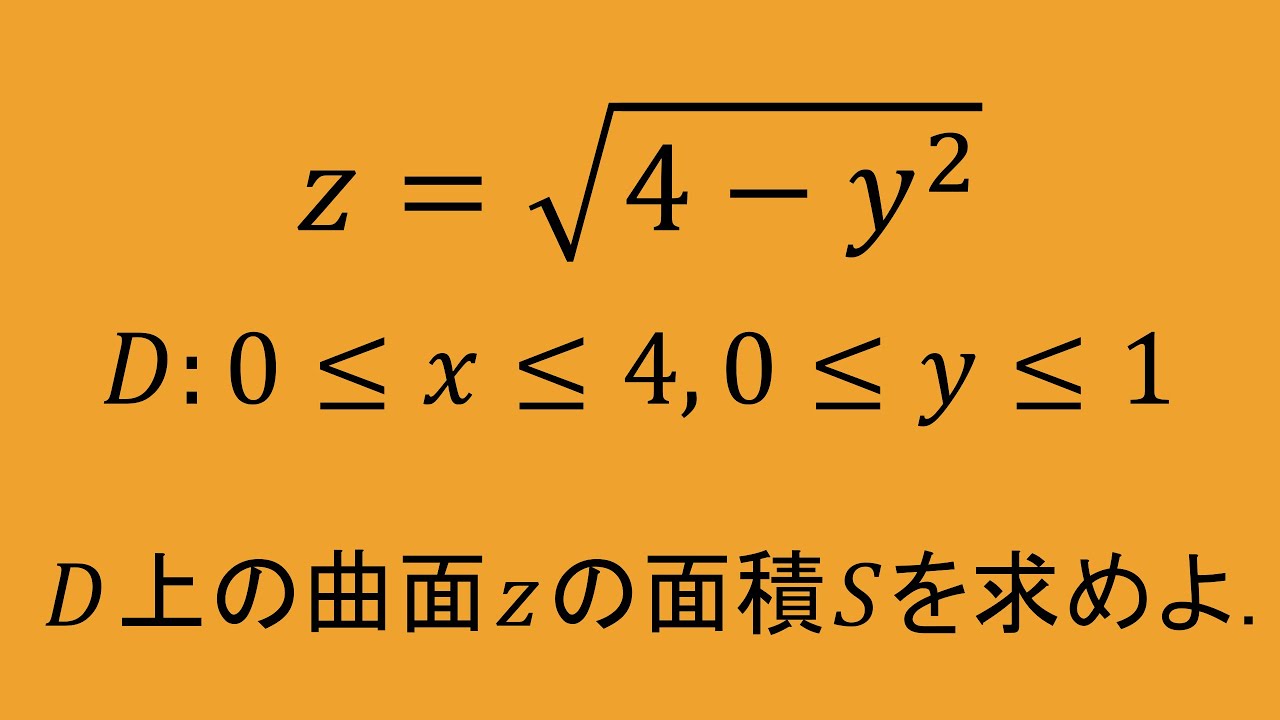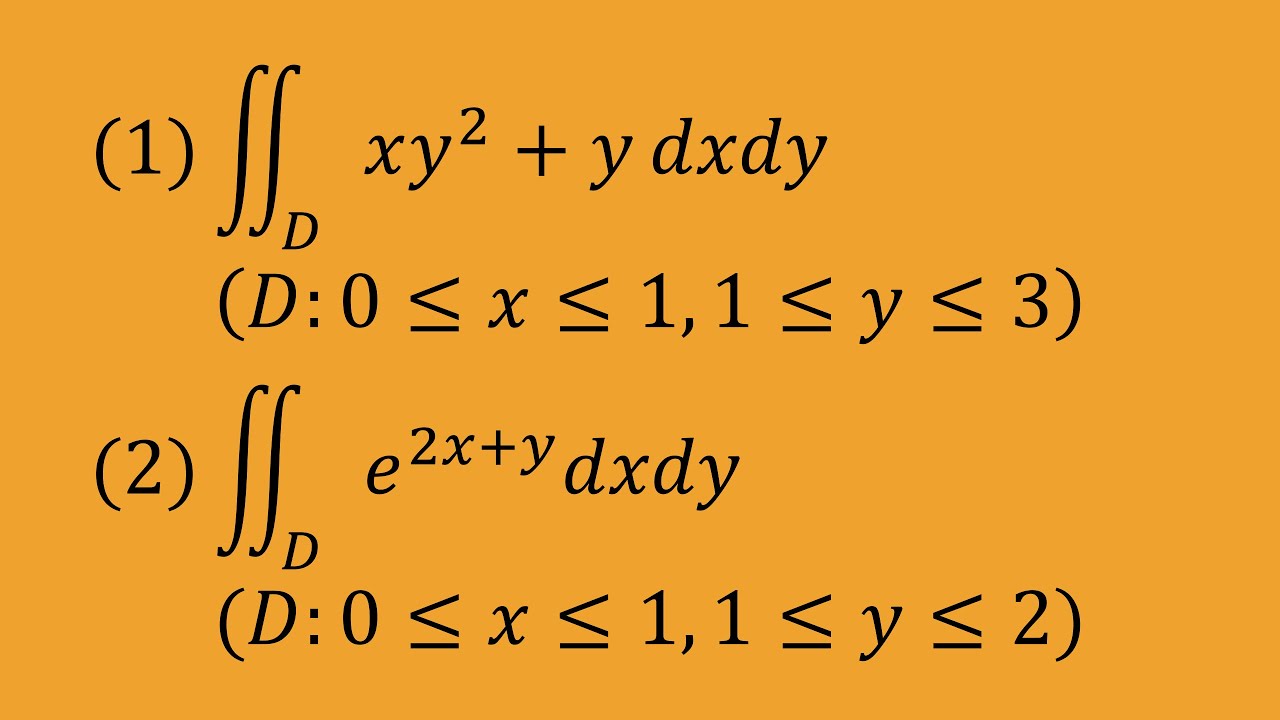問題文全文(内容文):
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定1級#その他#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
$\int_0^\infty e{-x^2}dx = \frac{\sqrt x}{2}$
(1)$\int_1^\infty e^{-(x-1)^2}dx$
(2)$\frac{1}{\sqrt{2x}} \int_{-\infty}^\infty e^{- \frac{x^2}{2}}dx$
(3)$\frac{1}{\sigma \sqrt{2x}} \int_{-\infty}^\infty xe^{-\frac{(x-\mu)^2}{2 \sigma^2}}dx$
投稿日:2020.11.17