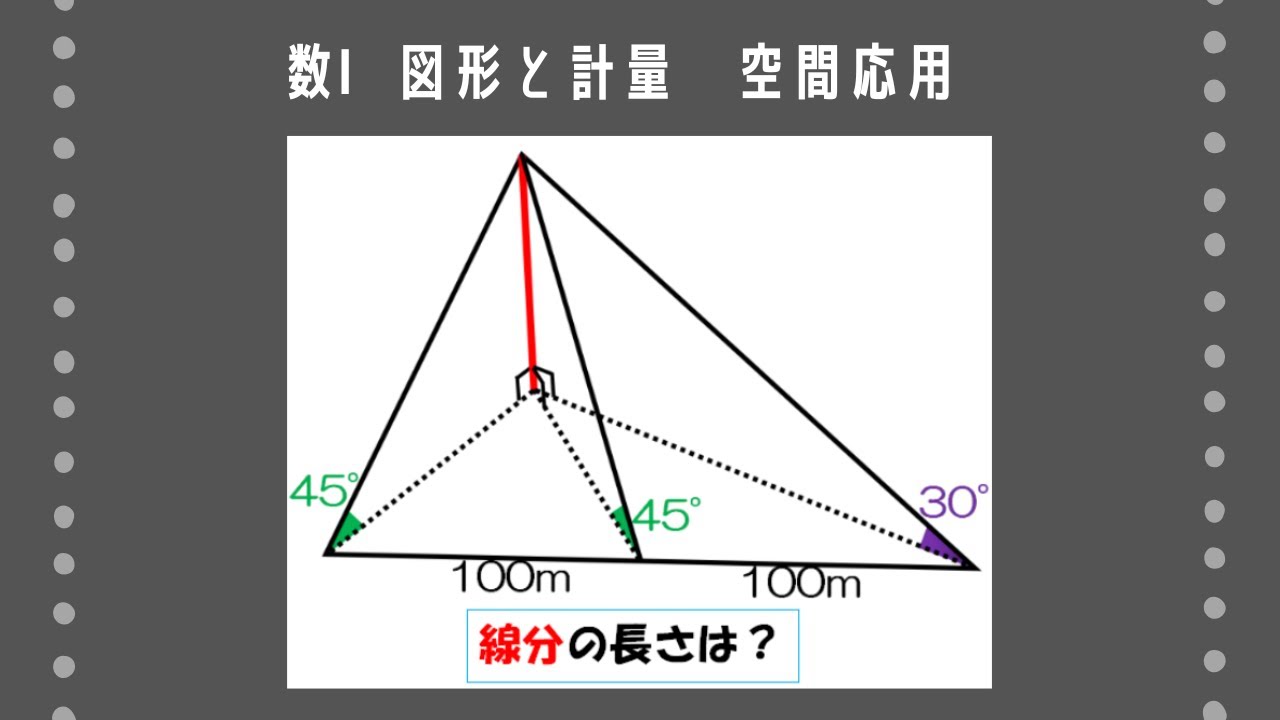
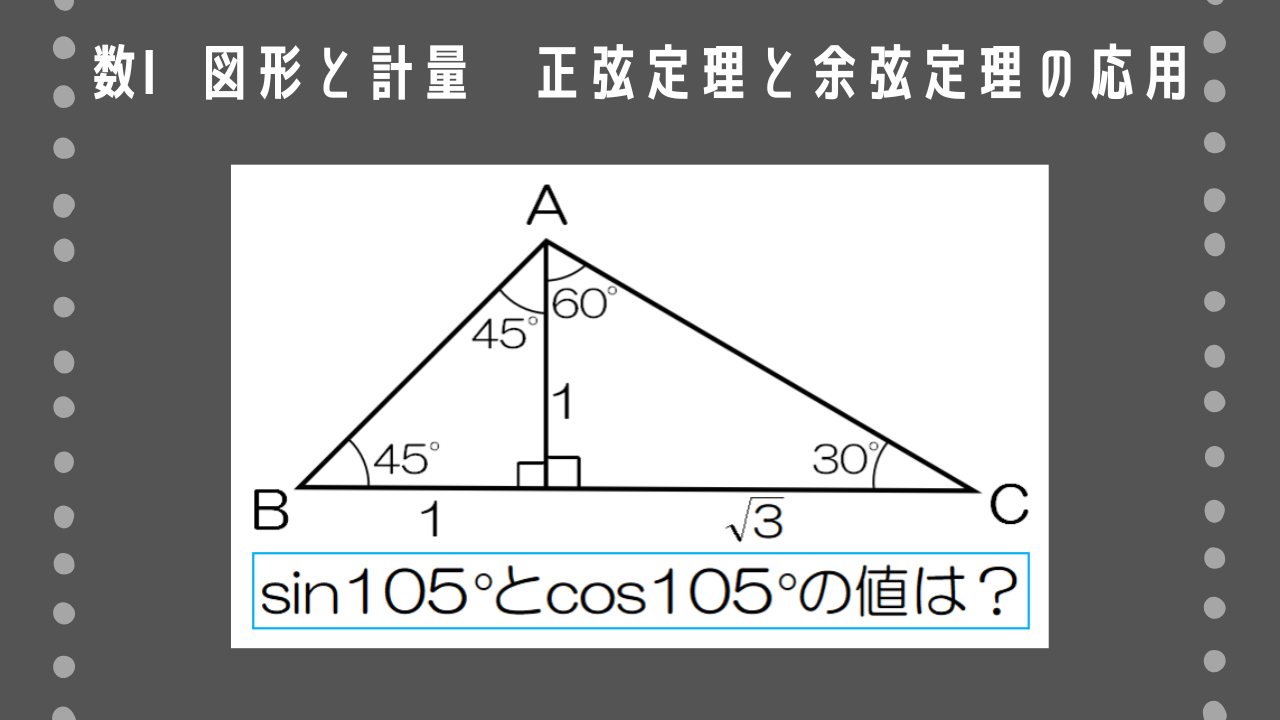
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
投稿日:2022.08.10