これなにしてるん？

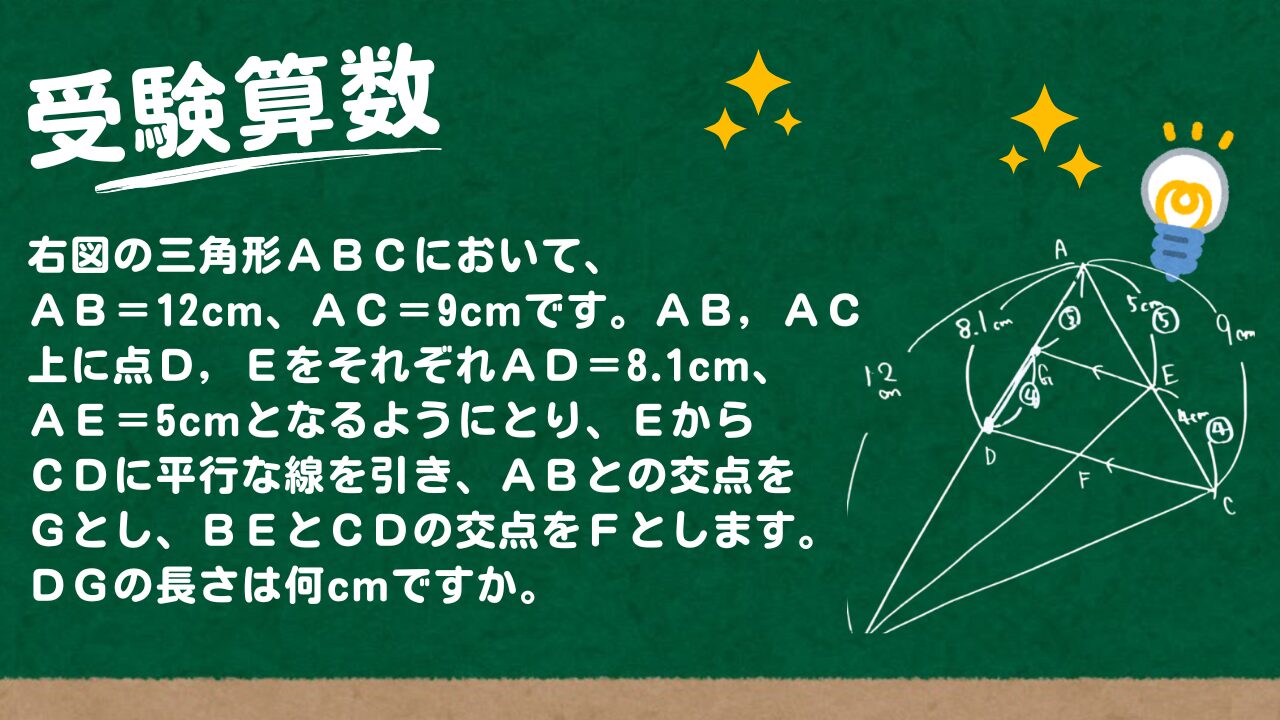
問題文全文(内容文)：
円に内接する正多角形

単元： #算数(中学受験)#数学(中学生)#中１数学#数Ⅰ#図形と計量#平面図形#図形の移動#平面図形その他#平面図形#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
円に内接する正多角形

投稿日：2024.11.03

＜関連動画＞

連除法【続編】中学受験算数「最小公倍数と最大公約数を完全マスター！」

単元： #算数(中学受験)#計算と数の性質#約数・倍数を利用する問題

指導講師：中学受験算数・高校受験数学けいたくチャンネル

問題文全文(内容文)：
三つの連除法【続編】

12と42と72の最大公約数と最小公倍数は?

この動画を見る　

【小６　算数】　　小６－１２　　対称な形①

単元： #算数(中学受験)#平面図形その他

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
ある形に折り目を作って、両側がピッタリ重なる形を① ＿＿＿といってその折り目を② ＿＿＿っていうんだ！

頂点Bに対応するのは③ ＿＿＿で、
辺$CD$に対応するのは④ ＿＿＿。
ちなみに、頂点$C$とFをつなぐと、
直線アイと⑤ ＿＿＿に交わる。
⑥ ① ＿＿＿＿＿＿な形を書こう！！
（コンパス→青、定規→赤）
※図は動画内参照

この動画を見る　

小６基礎トレ６月１８日⑧「線分の比」

単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例

指導講師：重吉

問題文全文(内容文)：
線分の比に関して解説していきます.

この動画を見る　

【中学受験問題に挑戦】88　（”大人”は頭の体操）　面積から角度

単元： #算数(中学受験)#平面図形#角度と面積

指導講師：算数・数学ちゃんねる

問題文全文(内容文)：
問題文
角Cの面積は？
「A」と「B」の面積は等しい。
※図は動画内参照

この動画を見る　

四谷大塚予習シリーズ「有名校対策」P108練習問題①

単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算

指導講師：重吉

問題文全文(内容文)：
（1）
Aくんが問題を解き終わったときのBくんの残っている問題数を求めよ

（2）
問題を全部解く日数の比を求めよ

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> これなにしてるん？

＜関連動画＞

連除法【続編】中学受験算数「最小公倍数と最大公約数を完全マスター！」

【小６ 算数】 小６－１２ 対称な形①

小６基礎トレ６月１８日⑧「線分の比」

【中学受験問題に挑戦】88 （”大人”は頭の体操） 面積から角度

四谷大塚予習シリーズ「有名校対策」P108練習問題①