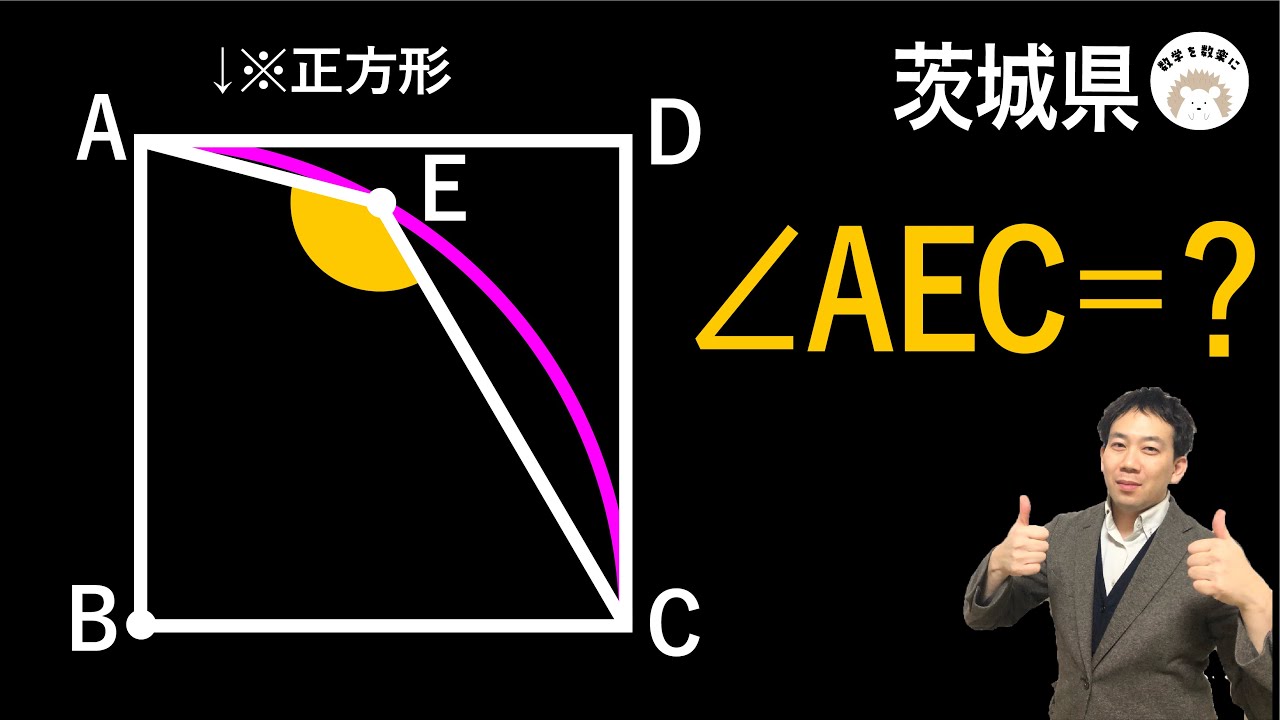
問題文全文(内容文):
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
第1問\ [3] 外接円の半径が3である$\triangle ABC$を考える。点Aから直線BCへ引いた垂線と直線BC
との交点をDとする。
(1)$AB=5, AC=4$とする。このとき$\sin\angle ABC=\frac{\boxed{ソ}}{\boxed{タ}}, AD=\frac{\boxed{チツ}}{\boxed{テ}}$ である。
(2) 2辺AB,ACの長さの間に$2AB+AC=14$の関係があるとする。
このとき、ABの長さの取り得る値の範囲は$\boxed{ト} \leqq AB \leqq \boxed{ナ}$であり、
$AD=\frac{\boxed{ニヌ}}{\boxed{ネ}}AB^2+\frac{\boxed{ノ}}{\boxed{ハ}}AB$と表せるので、ADの長さの最大値は$\boxed{ヒ}$である。
2022共通テスト数学過去問
投稿日:2022.01.16