【受験算数】平面図形：東京都市大学付属2020年度第4回 大問4 比の問題！ - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 算数(中学受験) > 平面図形 > 相似と相似を利用した問題 > 【受験算数】平面図形：東京都市大学付属2020年度第4回 大問4　比の問題！

【受験算数】平面図形：東京都市大学付属2020年度第4回 大問4　比の問題！

問題文全文(内容文)：
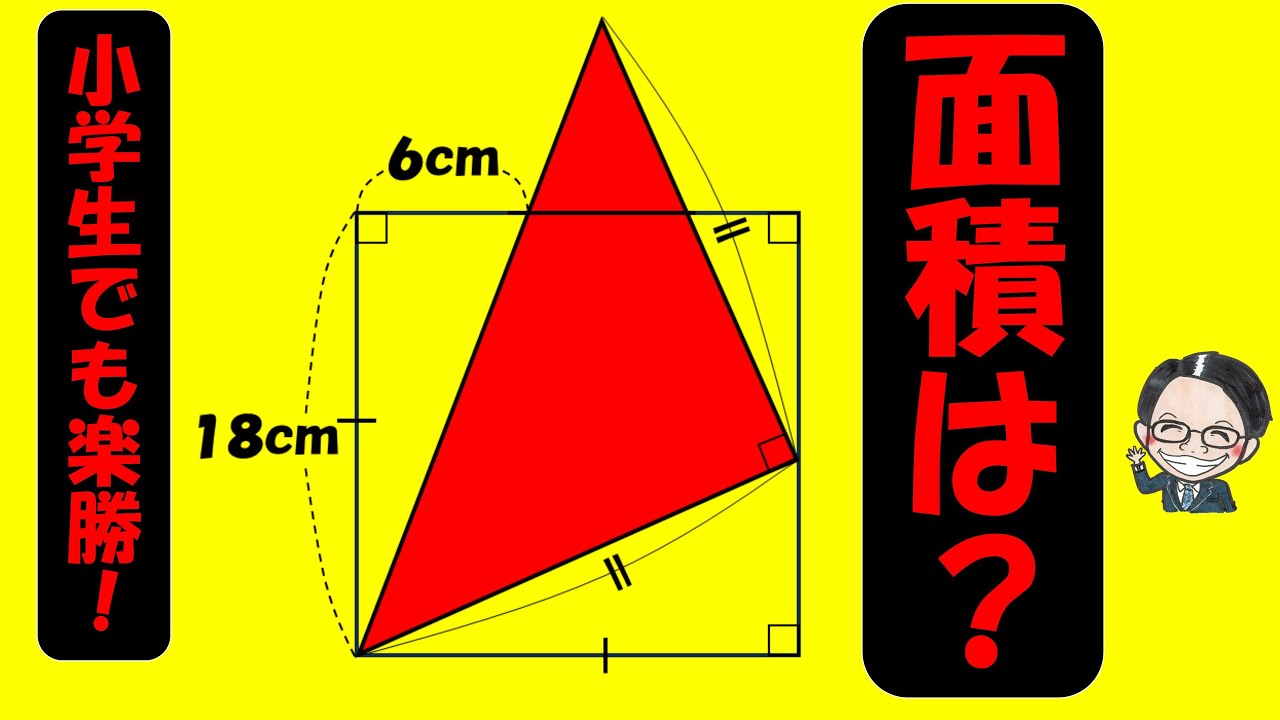
下の図のように、長方形ABCDとAE=EFである直角二等辺三角形AEFを組み合わせで、点E,Fはそれぞれ辺BC上、辺CD上にあります。また辺AD上、辺BC上にそれぞれ点G,Hを、四角形ABHGが正方形になるように取り、AFとGHが交わった点をIとすると、GI：IH=1：3になります。
(問1)BE：EHを、もっとも簡単な整数の比で答えよう。
(問2)直角二等辺三角形AEFの面積は、正方形ABHGの何倍ですか。
チャプター：

0:00 オープニング
0:05 問題文
0:20 補助線を引く発想
0:50 問題解説(1)
1:57 問題解説(2)
2:53 名言

単元： #算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#東京都市大学付属中学
指導講師： 理数個別チャンネル
問題文全文(内容文)：
下の図のように、長方形ABCDとAE=EFである直角二等辺三角形AEFを組み合わせで、点E,Fはそれぞれ辺BC上、辺CD上にあります。また辺AD上、辺BC上にそれぞれ点G,Hを、四角形ABHGが正方形になるように取り、AFとGHが交わった点をIとすると、GI：IH=1：3になります。
(問1)BE：EHを、もっとも簡単な整数の比で答えよう。
(問2)直角二等辺三角形AEFの面積は、正方形ABHGの何倍ですか。
投稿日：2021.02.14

＜関連動画＞

【SPX小5算数51-F04】速さに関する問題(A1)：学校に行く 【SPX W-支援】

アイキャッチ画像
単元： #算数(中学受験)#速さ#旅人算・通過算・流水算
教材： #SPX#中学受験教材#5年算数W-支援
指導講師： 受験算数の森
問題文全文(内容文)：
兄と弟は同時に家を出発して、家から1800m離れた学校までそれぞれ一定の速さで進みました。兄が学校についたとき、弟は学校まであと300mのところにいました。兄と弟の速さの比は何対何ですか。
この動画を見る　

中学受験算数「相似②」小学４年生～６年生対象【毎日配信】

アイキャッチ画像
単元： #算数(中学受験)#平面図形#相似と相似を利用した問題
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
第46回相似②

例題
次の図の平行四辺形ABCDで、AE:ED＝2:3 であるとき、次の線分の長さの比を、 最も簡単 な 整数の比で表しなさい。
この動画を見る　

50%＋50はいくらですか？

アイキャッチ画像
単元： #算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
50%＋50はいくらか解説していきます。
この動画を見る　

【受験算数】場合の数：不定方程式！　Aは1個35円、Bは1個45円です。律子は1260円の所持金をちょうど全部使って2種類とも買うつもりです。A,Bをそれぞれ何個ずつ買うことができますか。

アイキャッチ画像
単元： #算数(中学受験)#場合の数#場合の数
教材： #SPX#6年算数W-支援#中学受験教材
指導講師： 理数個別チャンネル
問題文全文(内容文)：
A,Bの2種類の品物があります。Aは1個35円、Bは1個45円です。律子は1260円の所持金をちょうど全部使って、2種類とも買うつもりです。A,Bをそれぞれ何個ずつ買うことができますか。すべての場合を答えなさい。
この動画を見る　

【受験算数】四則計算：7/8-5/6×(□-3/4)=1/2：神大附属(2019年度)の過去問を使って四則演算の逆算の手順をマスター！

アイキャッチ画像
単元： #算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#神奈川大学附属中学
指導講師： 理数個別チャンネル
問題文全文(内容文)：
$\dfrac{7}{8}-\dfrac{5}{6}\times \left(\Box-\dfrac{3}{4}\right)=\dfrac{1}{2}$
これを解け.
この動画を見る　
PAGE TOP