問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
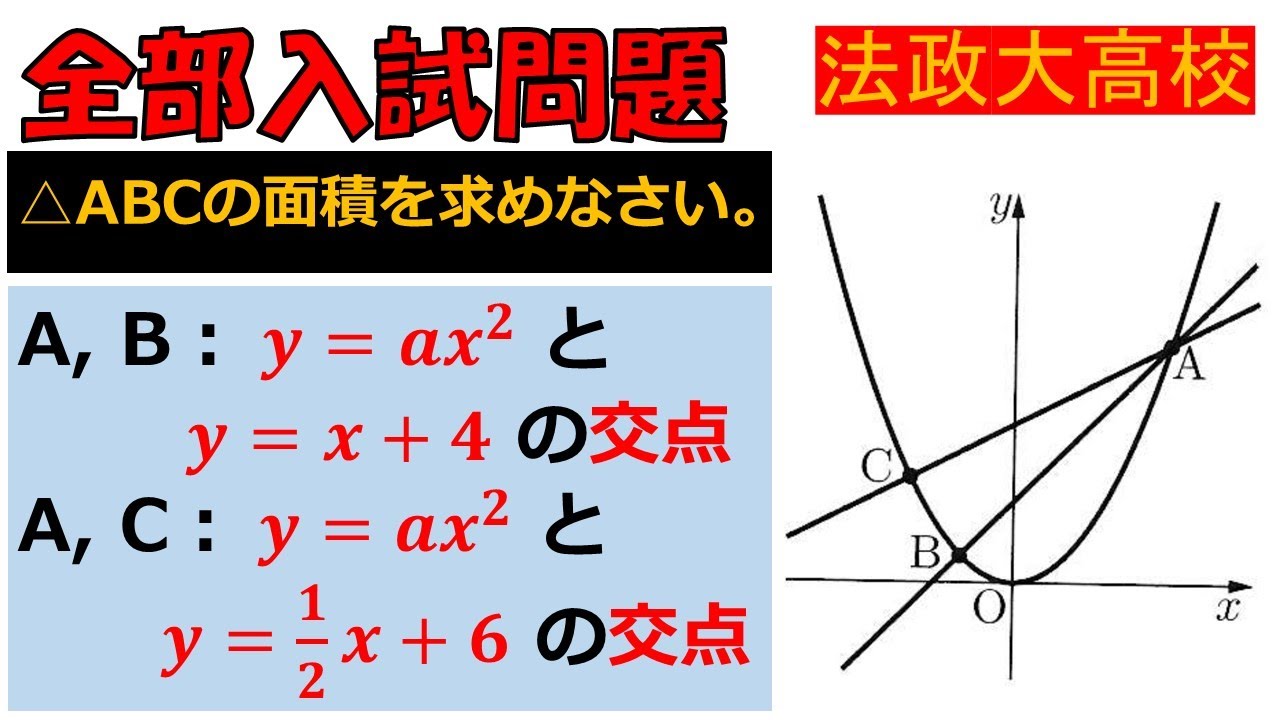
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
入試問題 大阪教育大学附属高等学校池田校舎
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
入試問題 大阪教育大学附属高等学校池田校舎
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
投稿日:2021.02.25