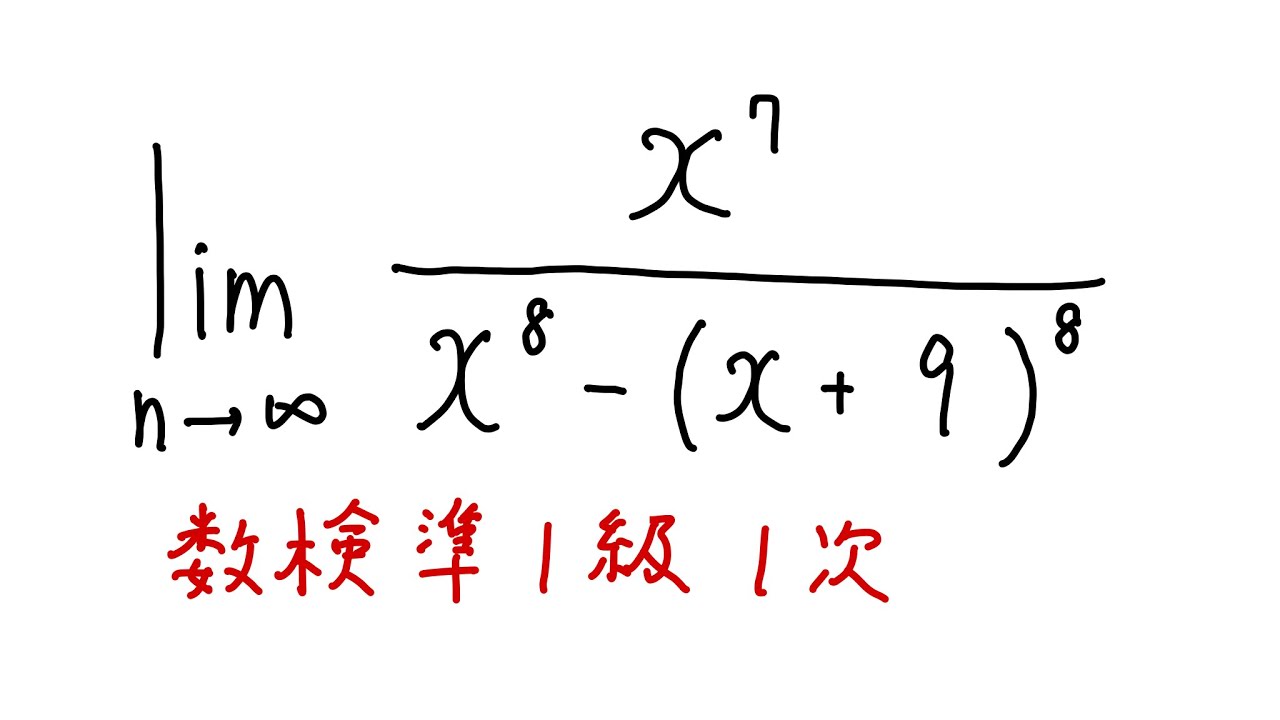問題文全文(内容文):
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
投稿日:2019.01.23