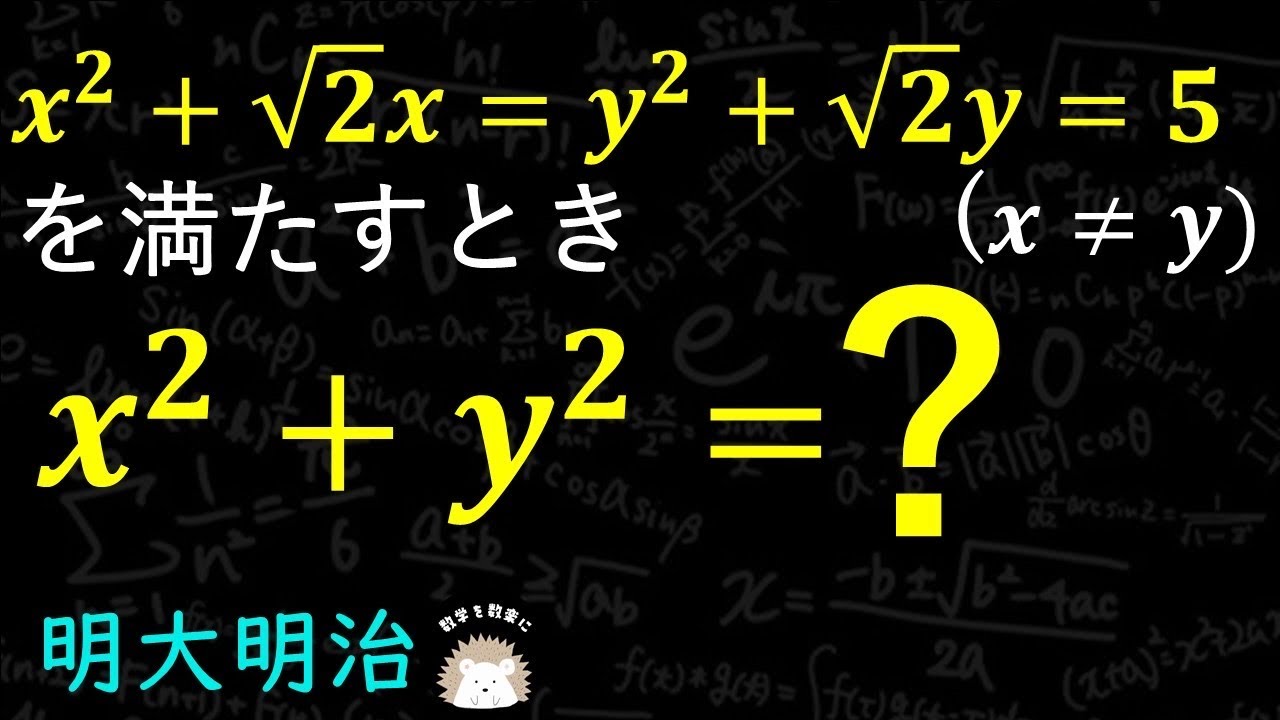【#6】【因数分解100問】基礎から応用まで！(51)〜(60)【解説付き】

問題文全文(内容文)：
(51)

a^{2} (b + c) + b^{2} (c + a) + c^{2} (a + b) + 3 a b c

(52)

a b (a + b) + b c (b + c) + c a (c + a) + 3 a b c

(53)

x^{4} - 15 x^{2} + 9

(54)

x^{4} + x^{2} y^{2} + y^{4}

(55)

x^{4} + 4 y^{4}

(56)

(a^{2} + a + 1) (a^{2} - a + 1)

(57)

(x + 1) (x - 1) (x + 3) (x - 3)

(58)

(x - 3)^{3}

(59)

(x + 2) (x - 2) (x - 3)

(60)

(2 x^{2} + 4 x y + 2 y^{2} + 2 x + 2 y + 1) (2 x + 2 y + 1)

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
(51)

a^{2} (b + c) + b^{2} (c + a) + c^{2} (a + b) + 3 a b c

(52)

a b (a + b) + b c (b + c) + c a (c + a) + 3 a b c

(53)

x^{4} - 15 x^{2} + 9

(54)

x^{4} + x^{2} y^{2} + y^{4}

(55)

x^{4} + 4 y^{4}

(56)

(a^{2} + a + 1) (a^{2} - a + 1)

(57)

(x + 1) (x - 1) (x + 3) (x - 3)

(58)

(x - 3)^{3}

(59)

(x + 2) (x - 2) (x - 3)

(60)

(2 x^{2} + 4 x y + 2 y^{2} + 2 x + 2 y + 1) (2 x + 2 y + 1)

投稿日：2022.04.06

＜関連動画＞

2023高校入試解説37問目早稲田実業最初の一問　因数分解

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
因数分解せよ

(x + 1) a^{2} - 2 x a + x - 1

2023早稲田実業学校

この動画を見る　

30秒ほどで高校入試の悪問を解説する動画～全国入試問題解法 #shorts #数学 #高校受験

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：高校入試から見た数学の世界「全部入試問題」by しろたん

問題文全文(内容文)：

(x^{2} + 2022)^{2} - 4092529 x^{2}

を因数分解しなさい.

中大杉並高校過去問

この動画を見る　

気付けば一瞬！！2通りで解説。式の値　2023駒込高校

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：

x = \frac{- b + \sqrt{b^{2} + 4 a}}{2 a}

のとき

a x^{2} + b x = ?

2023駒込高等学校

この動画を見る　

式の値　昭和学院秀英

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：

x^{2} y + x y^{2} = 1

\frac{y}{x} + \frac{x}{y} = 6

のとき　x+y=?

昭和学院秀英高等学校

この動画を見る　

これでも高校入試　因数分解　久留米大附設

単元： #数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)

指導講師：数学を数楽に

問題文全文(内容文)：
因数分解せよ

x^{2} + (a + 7) x - 6 (a - 2) (a + 1)

久留米大学附設高等学校

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 【#6】【因数分解100問】基礎から応用まで！(51)〜(60)【解説付き】

＜関連動画＞

2023高校入試解説37問目 早稲田実業最初の一問 因数分解

30秒ほどで高校入試の悪問を解説する動画～全国入試問題解法 #shorts #数学 #高校受験

気付けば一瞬！！2通りで解説。式の値 2023駒込高校

式の値 昭和学院秀英

これでも高校入試 因数分解 久留米大附設