 中3数学
中3数学
 中3数学
中3数学
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円錐の側面の距離

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、底面の直径ABが6㎝、母線の長さが12㎝の円錐がある。母線OA上に点CをOC=4√2㎝となるようにとり、点Cから点Bまでの最短コースで結ぶとき、次の問いに答えなさい。
(1)この最短コースの長さを求めなさい。
(2)線分AC,弧AB、最短コースCBで囲まれる部分(図の斜線部分)の面積を求めなさい。
この動画を見る
右の図のように、底面の直径ABが6㎝、母線の長さが12㎝の円錐がある。母線OA上に点CをOC=4√2㎝となるようにとり、点Cから点Bまでの最短コースで結ぶとき、次の問いに答えなさい。
(1)この最短コースの長さを求めなさい。
(2)線分AC,弧AB、最短コースCBで囲まれる部分(図の斜線部分)の面積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 柱の展開

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、辺ADと辺BCが平行で、AD=10㎝、BC=4㎝、AB=CD=5㎝の台形ABCDを底面とし、AE=BF=CG=DH=7cmを高さとする四角柱である。このとき、次の問いに答えなさい。
(1)この四角柱の側面上に、頂点Eから辺BFと辺CGに交わるように、頂点Dまで引く。このような線のうち、最も短い線の長さを求めなさい。
(2)平行な2つの線分AD,FGを含む平面でこの四角柱を切り、2つの立体に分けるとき、頂点Bを含む立体の体積を求めなさい。
この動画を見る
右の図は、辺ADと辺BCが平行で、AD=10㎝、BC=4㎝、AB=CD=5㎝の台形ABCDを底面とし、AE=BF=CG=DH=7cmを高さとする四角柱である。このとき、次の問いに答えなさい。
(1)この四角柱の側面上に、頂点Eから辺BFと辺CGに交わるように、頂点Dまで引く。このような線のうち、最も短い線の長さを求めなさい。
(2)平行な2つの線分AD,FGを含む平面でこの四角柱を切り、2つの立体に分けるとき、頂点Bを含む立体の体積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円柱と四角錐
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
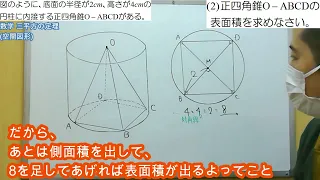
右の図のように、底面の半径が2cm、高さが4cmの円柱に内接する正四角錐O-ABCDがある。
(1)正四角錐O-ABCDの底面積を求めなさい。
(2)正四角錐O-ABCDの表面積を求めなさい。
この動画を見る
右の図のように、底面の半径が2cm、高さが4cmの円柱に内接する正四角錐O-ABCDがある。
(1)正四角錐O-ABCDの底面積を求めなさい。
(2)正四角錐O-ABCDの表面積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円錐と球

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、底面の半径が5㎝、高さが12㎝の円錐に、球Oが内接している。このとき、次の問いに答えなさい。
(1)球Oの半径を求めなさい。
(2)球Oが側面と接している部分の曲線の長さを求めなさい。
この動画を見る
右の図のように、底面の半径が5㎝、高さが12㎝の円錐に、球Oが内接している。このとき、次の問いに答えなさい。
(1)球Oの半径を求めなさい。
(2)球Oが側面と接している部分の曲線の長さを求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 正四面体
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
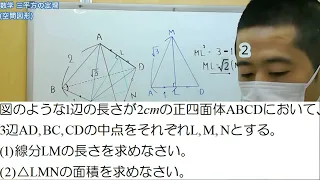
右の図のような1辺の長さが2㎝の正四面体ABCDにおいて、3辺AD,BC,CDの中点をそれぞれL,M,Nとする。
(1)線分LMの長さを求めなさい。
(2)△LMNの面積を求めなさい。
この動画を見る
右の図のような1辺の長さが2㎝の正四面体ABCDにおいて、3辺AD,BC,CDの中点をそれぞれL,M,Nとする。
(1)線分LMの長さを求めなさい。
(2)△LMNの面積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 関数上の外接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数y=-2x+4のグラフがx軸と交わる点をA,y軸と交わる点をBとする。Oを原点とするとき、△OABの外接円の半径を求めなさい。
この動画を見る
関数y=-2x+4のグラフがx軸と交わる点をA,y軸と交わる点をBとする。Oを原点とするとき、△OABの外接円の半径を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 放物線と直線の交点の面積

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、放物線$y=\displaystyle \frac{x^2}{2}$と直線$y=\displaystyle \frac{x}{2}+6$が2点A, Bで交わっていて、原点O(0,0)から直線ABに引いた垂線をOHとする。
(1)△OABの面積を求めなさい。
(2)垂線OHの長さを求めなさい。
この動画を見る
右の図のように、放物線$y=\displaystyle \frac{x^2}{2}$と直線$y=\displaystyle \frac{x}{2}+6$が2点A, Bで交わっていて、原点O(0,0)から直線ABに引いた垂線をOHとする。
(1)△OABの面積を求めなさい。
(2)垂線OHの長さを求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 放物線と直線の交点の距離

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の放物線と直線は異なる2点で交わる。その交点をそれぞれA, Bとするとき、線分ABの長さを求めなさい。
(1)$y=x^2$, $y=x+2$
(2)$y=-\displaystyle \frac{x^2}{2}$, $y=-x-4$
この動画を見る
次の放物線と直線は異なる2点で交わる。その交点をそれぞれA, Bとするとき、線分ABの長さを求めなさい。
(1)$y=x^2$, $y=x+2$
(2)$y=-\displaystyle \frac{x^2}{2}$, $y=-x-4$
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 垂線の長さ

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2点A,Bを通る直線に原点O(0,0)から引いた垂線OHの長さを求めなさい。
(1)$A(2,0)$, $B(0,6)$
(2)$A(\dfrac{25}{3},0)$, $B(0,\dfrac{25}{4})$
この動画を見る
次の2点A,Bを通る直線に原点O(0,0)から引いた垂線OHの長さを求めなさい。
(1)$A(2,0)$, $B(0,6)$
(2)$A(\dfrac{25}{3},0)$, $B(0,\dfrac{25}{4})$
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 長方形の回転

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=4cm, BC=6cmの長方形ABCDがある。直線L上において、この長方形を右の図のように、点Bが再び直線L上にくるまですべることなく転がす。
(1)点Bの軌跡の長さを求めなさい。
(2)長方形ABCDの対角線の交点をOとするとき、点Oの軌跡の長さを求めなさい。
この動画を見る
AB=4cm, BC=6cmの長方形ABCDがある。直線L上において、この長方形を右の図のように、点Bが再び直線L上にくるまですべることなく転がす。
(1)点Bの軌跡の長さを求めなさい。
(2)長方形ABCDの対角線の交点をOとするとき、点Oの軌跡の長さを求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 直角三角形の回転

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、AB=$1+\sqrt{3}$ cm、∠90°の直角二等辺三角形OABを、Oを中心として、時計の針の回転と同じ向きに30°だけ回転した図形を△OCDとする。AOとCDの交点をPとするとき、△PDOの面積を求めなさい。
この動画を見る
右の図のように、AB=$1+\sqrt{3}$ cm、∠90°の直角二等辺三角形OABを、Oを中心として、時計の針の回転と同じ向きに30°だけ回転した図形を△OCDとする。AOとCDの交点をPとするとき、△PDOの面積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 合同の利用
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
この動画を見る
右の図において、四角形の頂点A,B,C,DはBDを直径とする円Oの周上にあり、Eは直線BAとCDの交点で、辺DAは∠BDEを2等分している。DC=3cm、BD=6cmであるとき、辺DAの長さを求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形2

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
この動画を見る
右の図は、1辺の長さが9cmの正方形ABCDを、頂点Aが辺DC上の点Eに重なるように折り返したもので、PQは折り目の線である。
DE=3cmであるとき、次の問いに答えなさい。
(1)線分APの長さを求めなさい。
(2)線分BQの長さを求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 折り返した図形1
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
この動画を見る
右の図のように、円A,B,Cは縦4cm,横6cmの長方形の辺に接し、円AとCおよび円BとCはそれぞれ外接している。円A,Bの半径がともに1cmであるとき、円Cの半径を求めなさい。
【数学】中高一貫校問題集 幾何:三平方の定理:平面図形 内接円の半径2

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さがAB=7cm,BC=8cm,CA=9cmの△ABCがあり、円Oは△ABCに内接している。
(1)Aから辺BCに引いた垂線の長さを求めなさい。
(2)円Oの半径を求めなさい。
この動画を見る
3辺の長さがAB=7cm,BC=8cm,CA=9cmの△ABCがあり、円Oは△ABCに内接している。
(1)Aから辺BCに引いた垂線の長さを求めなさい。
(2)円Oの半径を求めなさい。
【数学】中高一貫校問題集 幾何:三平方の定理:平面図形 内接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図において、円Oは∠A=90°の直角三角形ABCに内接している。このとき、内接円Oの半径を求めなさい。
この動画を見る
右の図において、円Oは∠A=90°の直角三角形ABCに内接している。このとき、内接円Oの半径を求めなさい。
【数学】中高一貫校問題集2幾何179:三平方の定理:平面図形 外接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の△ABCについて、外接円の半径を求めなさい。
この動画を見る
次の△ABCについて、外接円の半径を求めなさい。
【数学】中高一貫校問題集2幾何178:三平方の定理:平面図形 2円の交点の長さ

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径が1cmの円Oと半径が$\sqrt{2}$cmの円O´が2点A,Bで交わっている。中心間の距離がOO´=2cmであるとき、線分ABの長さを求めなさい。
この動画を見る
半径が1cmの円Oと半径が$\sqrt{2}$cmの円O´が2点A,Bで交わっている。中心間の距離がOO´=2cmであるとき、線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何177:三平方の定理:平面図形 共通接線の長さ2
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
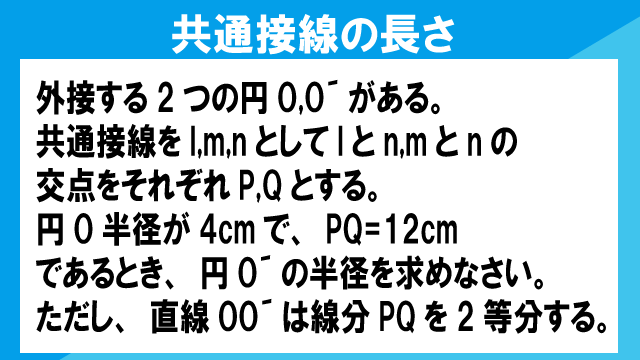
右の図のように、外接する2つの円O,O´がある。共通接線をl,m,nとしてlとn,mとnの交点をそれぞれP,Qとする。円O半径が4cmで、PQ=12cmであるとき、円O´の半径を求めなさい。ただし、直線OO´は線分PQを2等分する。
この動画を見る
右の図のように、外接する2つの円O,O´がある。共通接線をl,m,nとしてlとn,mとnの交点をそれぞれP,Qとする。円O半径が4cmで、PQ=12cmであるとき、円O´の半径を求めなさい。ただし、直線OO´は線分PQを2等分する。
ルートのかけ算はこうする?

ボボボーボ・ボーボボを因数分解すると?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
ボボボーボ・ボーボボを因数分解すると?
この動画を見る
下記質問の解説動画です
ボボボーボ・ボーボボを因数分解すると?
【数学】中高一貫校問題集2幾何176:三平方の定理:平面図形 共通接線の長さ1

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
この動画を見る
(1)図1で、2つの円O,O´は外接しており、A,Bは共通接線の接点である。O,O´の半径がそれぞれ5cm,2cmであるとき、線分ABの長さを求めなさい。
(2)図2で、A,Bは、2つの円O,O´の共通接線の接点である。O,O´の半径がそれぞれ5cm,3cmで、2つの円の中心間の距離が10cmであるとき、線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何175:三平方の定理:平面図形 四角形の面積

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(代数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
この動画を見る
次の四角形ABCDの面積を求めなさい。ただし、(1)で、AD//BCである。
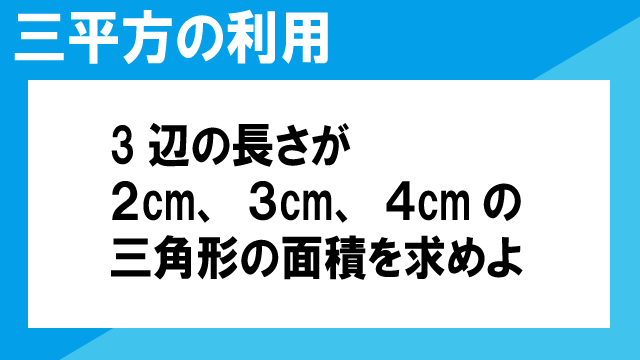
【数学】中高一貫校問題集2幾何174:三平方の定理:平面図形 三角形の面積+ヘロンの公式
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
この動画を見る
次の△ABCの面積を求めなさい。(3辺の長さが2cm、3cm、4cmの三角形の面積を求めよ)
この手があったか!分母の有理化

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{21}{\sqrt 7}=$
この動画を見る
$\frac{21}{\sqrt 7}=$
たすき掛けの裏技が使えないときは?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
たすき掛けの裏技が使えないときは?
$3x^2+15x+12=??$
この動画を見る
下記質問の解説動画です
たすき掛けの裏技が使えないときは?
$3x^2+15x+12=??$
これわかる?

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)$4xy^2+6x^2y^2-2xy$
(2)$x^2-x-12$
(3)$6x^2-6x-12$
この動画を見る
(1)$4xy^2+6x^2y^2-2xy$
(2)$x^2-x-12$
(3)$6x^2-6x-12$
【フル】因数分解の必殺技を伝授します
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
因数分解の必殺技を伝授します
(1)$4xy^2+6x^2y^2-2xy$
(2)$x^2-x-12$
(3)$6x^2-6x-12$
この動画を見る
因数分解の必殺技を伝授します
(1)$4xy^2+6x^2y^2-2xy$
(2)$x^2-x-12$
(3)$6x^2-6x-12$
【数学】中高一貫校問題集2幾何158:三平方の定理:線分の長さ

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
この動画を見る
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何157:三平方の定理:三角形の面積

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
この動画を見る
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
