問題文全文(内容文):
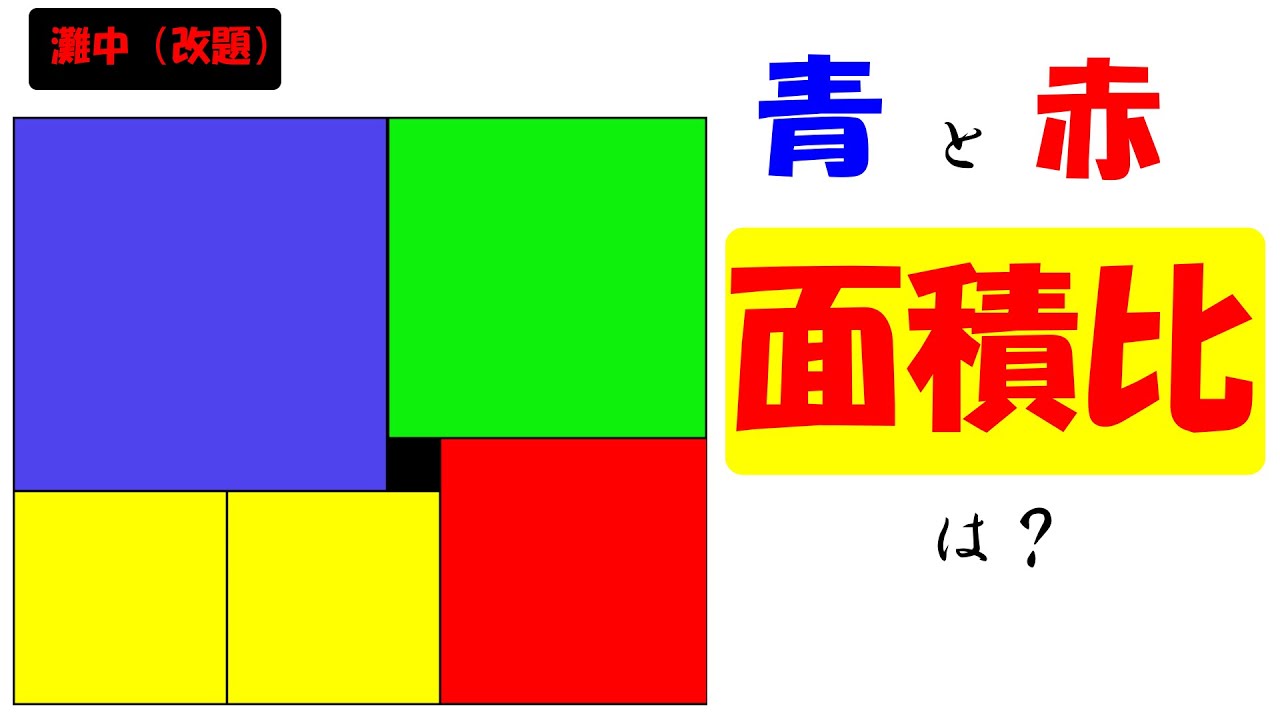
例1 面積は?
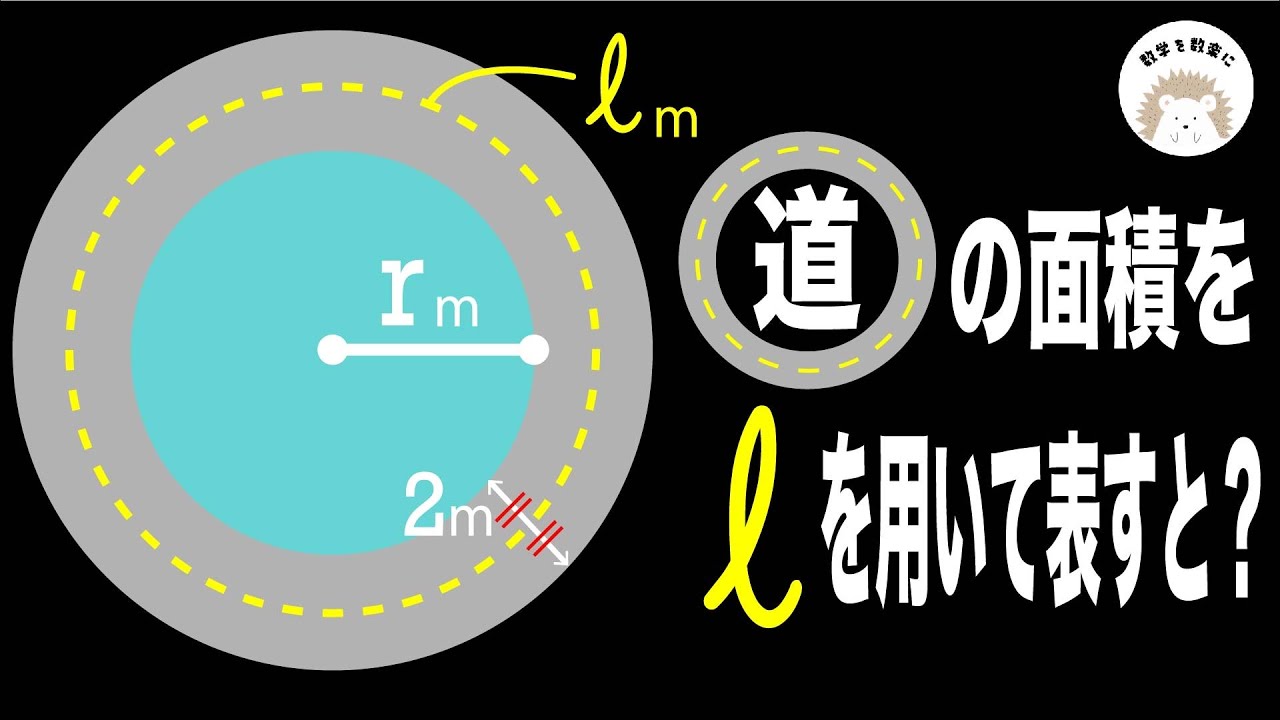
例2 面積は?
例3 斜線部の面積は?
単元卒業テスト
四角形ABQPの面積は?
*図は動画内参照
例1 面積は?
例2 面積は?
例3 斜線部の面積は?
単元卒業テスト
四角形ABQPの面積は?
*図は動画内参照
チャプター:
0:00 オープニング
0:13 今日の内容説明
1:46 30度がある時の基本法則
2:47 基本法則が成り立つ理由
4:34 例題1 30度・60度・90度の三角形の面積を求める
6:43 例題2 頂角が30度の二等辺三角形の面積を求める
8:35 例題3 頂角が150度の二等辺三角形の面積を求める
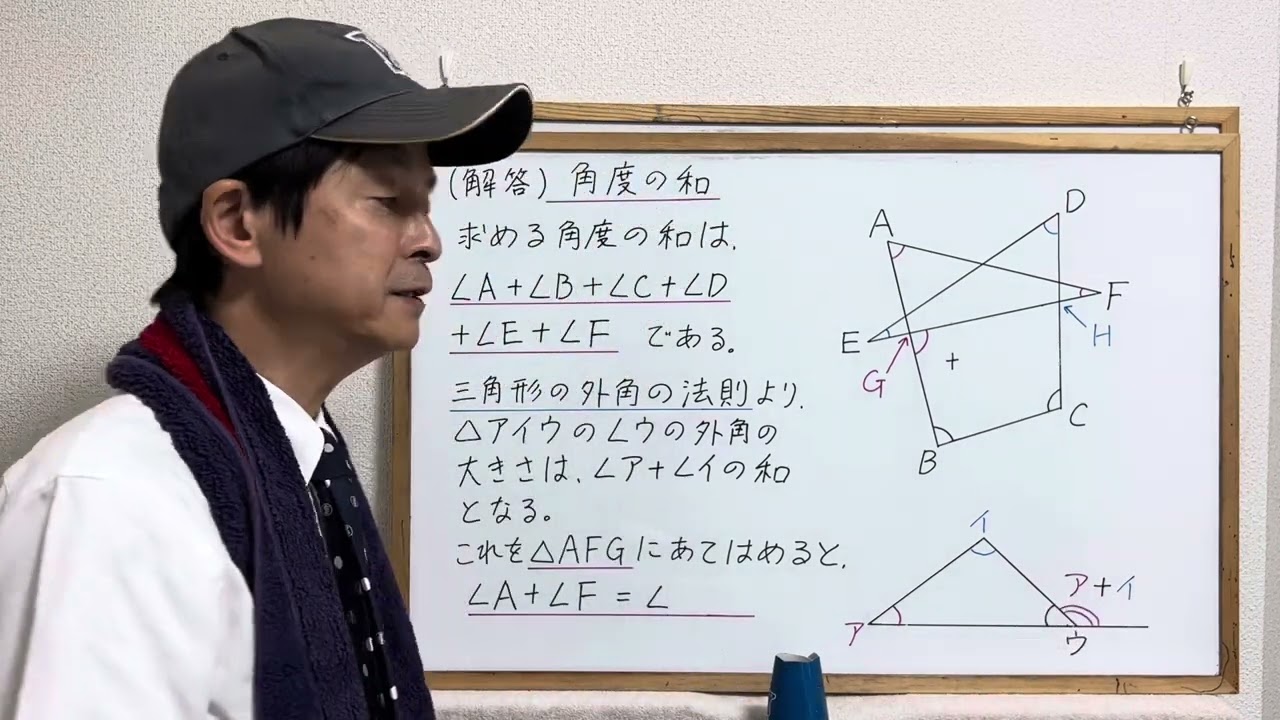
11:19 単元卒業テスト(応用問題) 問題提示
11:57 単元卒業テスト(応用問題) 問題解説
17:00 まとめ
17:41 家庭教師のアスピレーション 生徒募集のご案内
18:46 おすすめ動画紹介(ピアノ演奏付き)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
例1 面積は?
例2 面積は?
例3 斜線部の面積は?
単元卒業テスト
四角形ABQPの面積は?
*図は動画内参照
例1 面積は?
例2 面積は?
例3 斜線部の面積は?
単元卒業テスト
四角形ABQPの面積は?
*図は動画内参照
投稿日:2022.06.03