 【ゼロから理解できる】高校数学・物理
【ゼロから理解できる】高校数学・物理
 【ゼロから理解できる】高校数学・物理
【ゼロから理解できる】高校数学・物理
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【丁寧に解説】テストによく出る繁分数式(分数の中に分数)を解説!
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
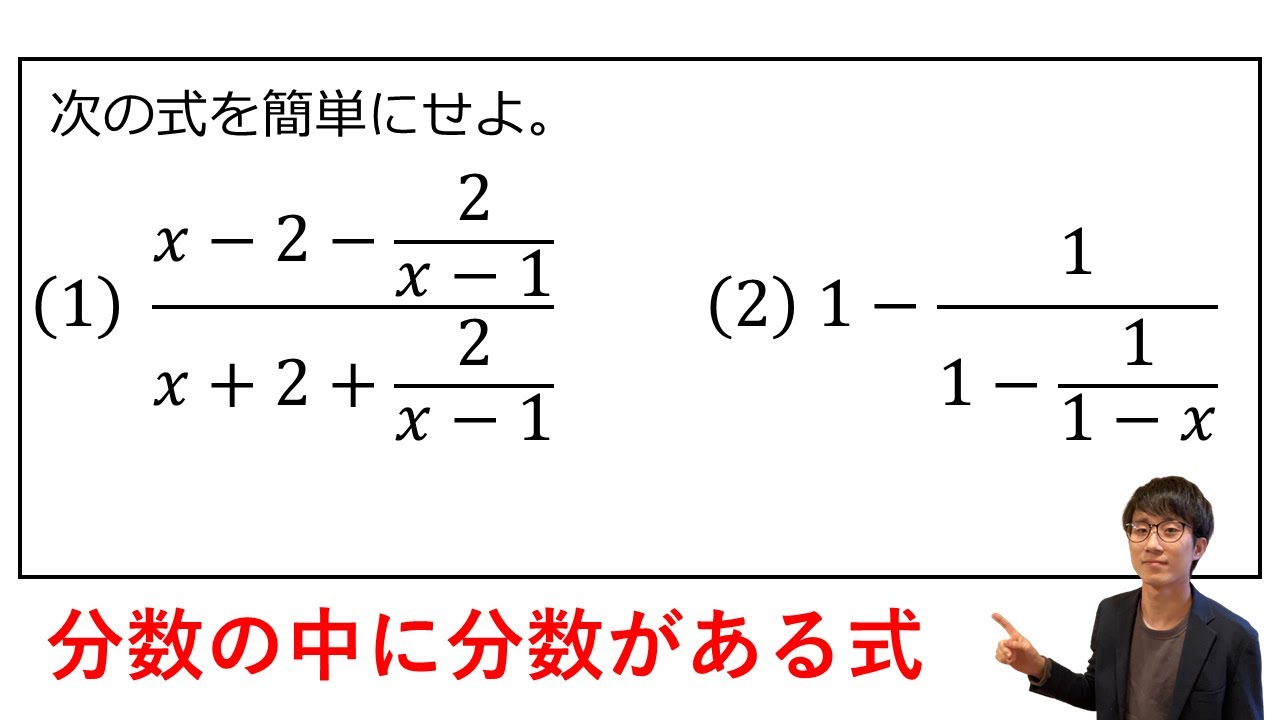
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)
$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)
$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
【ゼロからわかる】整式の割り算②(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
この動画を見る
次の問いに答えよ。
(1)
$x^2-6x+3$で割ると、商が$2x-3,$余りが$3x$である整数$A$を求めよ。
(2)
$x^3+3x^2+2x+1$を$B$で割ると、商が$x+1,$余りが$x+2$になる。
整数$B$を求めよ。
【ゼロからわかる】整式の割り算(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
この動画を見る
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
【わかりやすく】高校で習う展開公式②(高校数学Ⅰ)

【わかりやすく】高校で習う展開公式①(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ。
(1)$(x+2)(x^2-2x+4)$
(2)$(x-3y)(x^2+3xy+9y^2)$
この動画を見る
次の式を展開せよ。
(1)$(x+2)(x^2-2x+4)$
(2)$(x-3y)(x^2+3xy+9y^2)$
【ゼロからわかる】3乗の展開公式(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
この動画を見る
次の式を展開せよ。
(1)$(x+2)^3$
(2)$(3x-1)^3$
(3)$(2a-3b)^3$
【わかりやすく解説】中学の「展開」をおさらい!

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を展開せよ
(1)$(x+3)(2x-1)$
(2)$(x+3y)(x-3y)$
(3)$(x-5y)^2$
この動画を見る
次の式を展開せよ
(1)$(x+3)(2x-1)$
(2)$(x+3y)(x-3y)$
(3)$(x-5y)^2$
【ゼロからわかる】二項定理を3項で利用する(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式における、[ ]内の項の係数を求めよ。
$(x+2y-z)^6$ $[x^3y^2z]$
この動画を見る
次の式の展開式における、[ ]内の項の係数を求めよ。
$(x+2y-z)^6$ $[x^3y^2z]$
【わかりやすく解説】数学Ⅱ 二項定理で項の係数を求めよう!

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式における、[ ]内の項の係数を求めよ。
(1)
$(x+3)^5$ $[x^3]$
(2)
$(2x-3y)^6$ $[x^2y^4]$
この動画を見る
次の式の展開式における、[ ]内の項の係数を求めよ。
(1)
$(x+3)^5$ $[x^3]$
(2)
$(2x-3y)^6$ $[x^2y^4]$
【ゼロからわかる】二項定理の基本(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式を求めよ。
(1)
$(x+3)^4$
(2)
$(2a-b)^5$
この動画を見る
次の式の展開式を求めよ。
(1)
$(x+3)^4$
(2)
$(2a-b)^5$
【数学Ⅱ/積分】絶対値を含む定積分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の定積分を求めよ
$\displaystyle \int_{0}^{3} |x^2-1|dx$
この動画を見る
次の定積分を求めよ
$\displaystyle \int_{0}^{3} |x^2-1|dx$
【数学Ⅱ/積分】関数の決定(定積分)

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=3x^2+4x+\displaystyle \int_{-1}^{1} f(t) dt$
この動画を見る
次の等式を満たす関数$f(x)$を求めよ。
$f(x)=3x^2+4x+\displaystyle \int_{-1}^{1} f(t) dt$
【数学Ⅱ/積分】定積分で表された関数を求める

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の等式を満たす関数$f(x),$および定数$a$の値を求めよ。
$\displaystyle \int_{a}^{x} f(t) dt=x^2-3x-4$
この動画を見る
次の等式を満たす関数$f(x),$および定数$a$の値を求めよ。
$\displaystyle \int_{a}^{x} f(t) dt=x^2-3x-4$
【数学Ⅱ/積分】定積分で表された関数を微分

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の$x$の関数を微分せよ。
(1)
$\displaystyle \int_{1}^{x} (t^2-3t+2)dt$
(2)
$\displaystyle \int_{x}^{2} (3t^2-1)dt$
この動画を見る
次の$x$の関数を微分せよ。
(1)
$\displaystyle \int_{1}^{x} (t^2-3t+2)dt$
(2)
$\displaystyle \int_{x}^{2} (3t^2-1)dt$
【数学Ⅱ/積分】定積分の基本

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の定積分を求めよ。
(1)
$\displaystyle \int_{1}^{3} (-4x)dx$
(2)
$\displaystyle \int_{1}^{2} (x^2+3x+2)dx$
(3)
$\displaystyle \int_{-1}^{2} (x^2+3x)dx-\displaystyle \int_{-1}^{2} (x^2-x)dx$
この動画を見る
次の定積分を求めよ。
(1)
$\displaystyle \int_{1}^{3} (-4x)dx$
(2)
$\displaystyle \int_{1}^{2} (x^2+3x+2)dx$
(3)
$\displaystyle \int_{-1}^{2} (x^2+3x)dx-\displaystyle \int_{-1}^{2} (x^2-x)dx$
【数学Ⅱ/積分】原始関数を求める

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$F'(x)=6x^2+4x+3,F(0)=1$を満たす関数$F(x)$を求めよ。
この動画を見る
$F'(x)=6x^2+4x+3,F(0)=1$を満たす関数$F(x)$を求めよ。
【数学Ⅱ/積分】不定積分の基本

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不定積分を求めよ。
(1)
$\displaystyle \int (-2)dx$
(2)
$\displaystyle \int (3x+4)dx$
(3)
$\displaystyle \int (2t-1)^2dx$
この動画を見る
次の不定積分を求めよ。
(1)
$\displaystyle \int (-2)dx$
(2)
$\displaystyle \int (3x+4)dx$
(3)
$\displaystyle \int (2t-1)^2dx$
【数学Ⅰ/三角比】円に内接する四角形②
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
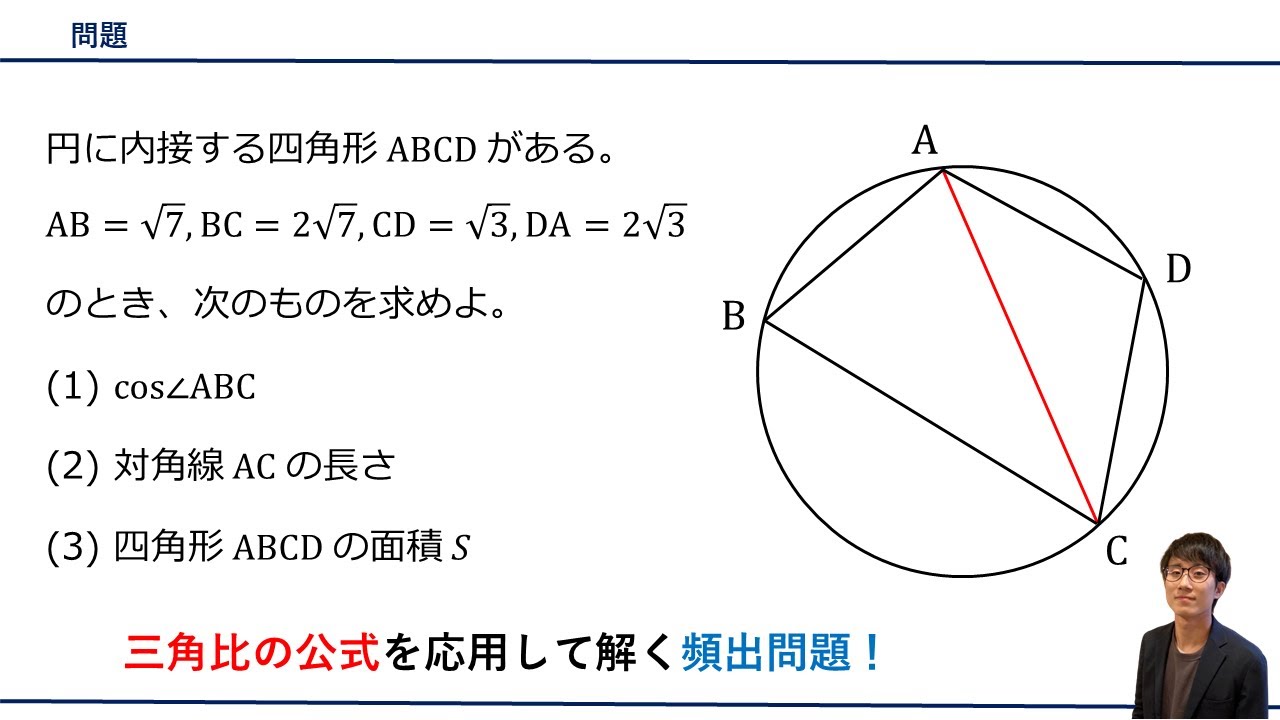
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
この動画を見る
円に内接する四角形$ABCD$がある。
$AB=\sqrt{ 7 },BC=2\sqrt{ 7 },CD=\sqrt{ 3 },DA=2\sqrt{ 3 }$のとき、次のものを求めよ。
(1)
$\cos\angle ABC$
(2)
対角線$AC$の長さ
(3)
四角形$ABCD$の面積$S$
【数学Ⅰ/三角比】円に内接する四角形①
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
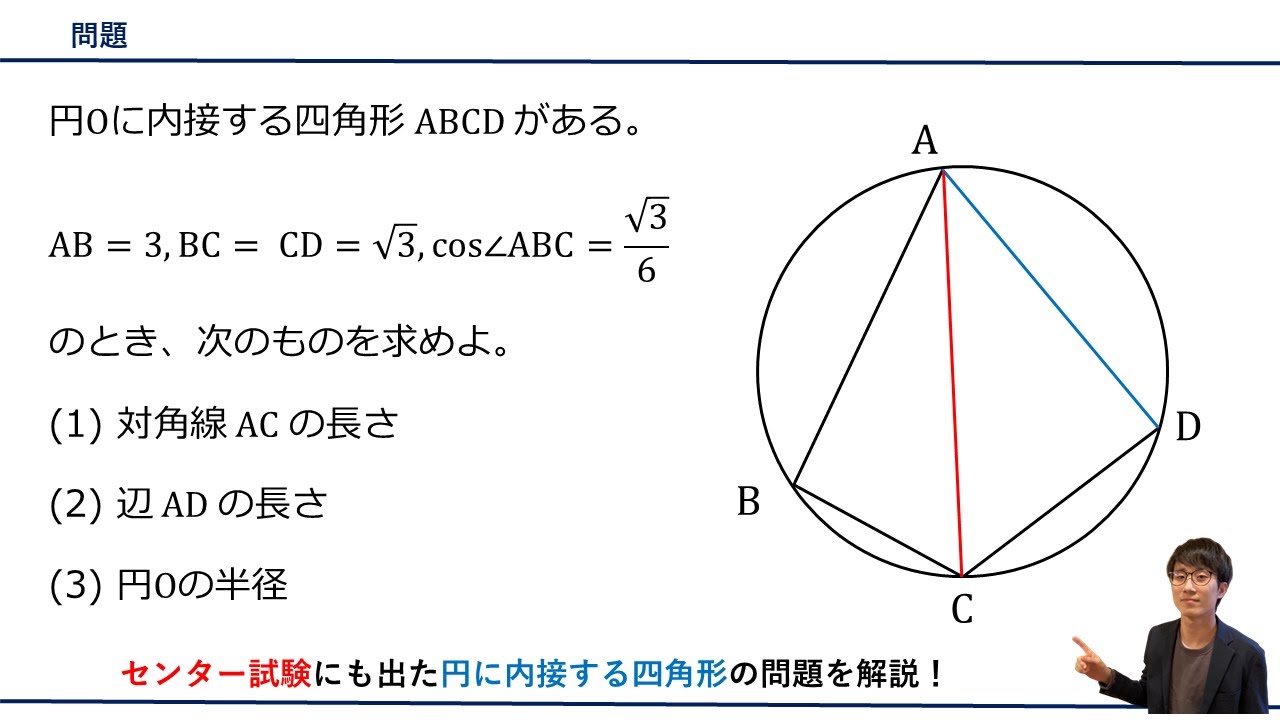
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
この動画を見る
円$O$に内接する四角形$ABCD$がある。
$AB=3,$ $BC=CD=\sqrt{ 3 },$ $\cos\angle ABC=\displaystyle \frac{\sqrt{ 3 }}{6}$のとき、次のものを求めよ。
(1)対角線$AC$の長さ
(2)辺$AD$の長さ
(3)円$O$の半径
【数学Ⅰ/三角比】正弦定理を使って辺の比を求める問題

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、$\displaystyle \frac{\sin A}{4}=\displaystyle \frac{\sin B}{5}=\displaystyle \frac{\sin C}{2}$が成立しているとき、次の問いに答えよ。
(1)3辺の比$a:b:c$を求めよ。
(2)$\cos B$の値を求めよ。
この動画を見る
$\triangle ABC$において、$\displaystyle \frac{\sin A}{4}=\displaystyle \frac{\sin B}{5}=\displaystyle \frac{\sin C}{2}$が成立しているとき、次の問いに答えよ。
(1)3辺の比$a:b:c$を求めよ。
(2)$\cos B$の値を求めよ。
【数学Ⅰ/三角比】余弦定理の使い方

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、次の値を求めよ。
(1)$a=2\sqrt{ 3 },b=3,c=30^{ \circ }$のとき、$C$。
(2)$a=8,b=5,c=7$のとき、$C$。
この動画を見る
$\triangle ABC$において、次の値を求めよ。
(1)$a=2\sqrt{ 3 },b=3,c=30^{ \circ }$のとき、$C$。
(2)$a=8,b=5,c=7$のとき、$C$。
【数学Ⅰ/三角比】正弦定理の使い方

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$\triangle ABC$において、$a=2\sqrt{ 2 },b=2,A=45^{ \circ }$のとき、$B$および外接円の半径$R$を求めよ。
この動画を見る
$\triangle ABC$において、$a=2\sqrt{ 2 },b=2,A=45^{ \circ }$のとき、$B$および外接円の半径$R$を求めよ。
【数学A/整数】 n進法→10進法(小数)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の数を10進法の小数で表せ。
(1)$0.101_{(2)}$
(2)$0.24_{(5)}$
この動画を見る
次の数を10進法の小数で表せ。
(1)$0.101_{(2)}$
(2)$0.24_{(5)}$
【数学A/整数】10進法をn進法で表す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の10進法を[ ]内の表し方で表せ。
(1)57 [2進法]
(2)83 [5進法]
この動画を見る
次の10進法を[ ]内の表し方で表せ。
(1)57 [2進法]
(2)83 [5進法]
◆わかりやすく◆数学A・整数 n進法を10進法で表す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の数を10進法で表せ。
(1)$1101_{(2)}$
(2)$231_{(4)}$
この動画を見る
次の数を10進法で表せ。
(1)$1101_{(2)}$
(2)$231_{(4)}$
【数学A/整数】方程式の整数解を求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
方程式$xy-3x+y+2=0$を満たす整数の組$(x,y)$を全て求めよ。
この動画を見る
方程式$xy-3x+y+2=0$を満たす整数の組$(x,y)$を全て求めよ。
【わかりやすく解説】等式を満たす自然数を求める(数学A・整数)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
等式$3x+4y=45$を満たす自然数$x,y$の組を全て求めよ。
この動画を見る
等式$3x+4y=45$を満たす自然数$x,y$の組を全て求めよ。
【テストによく出る】数学A 一次不定方程式(ユークリッドの互除法を使って特殊解を求める)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
不定方程式$90x-37y=1$の整数解を求めよ。
この動画を見る
不定方程式$90x-37y=1$の整数解を求めよ。
【0から理解できる】一次不定方程式を解説しました!(数学A・整数)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の不定方程式の整数解を求めよ。
(1)$5x-3y=1$
(2)$5x-3y=4$
この動画を見る
次の不定方程式の整数解を求めよ。
(1)$5x-3y=1$
(2)$5x-3y=4$
【数学A/整数】ユークリッドの互除法(文字式)

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。
この動画を見る
$7n+6$と$2n+3$の最大公約数が$3$になるような$20$以下の自然数$n$をすべて求めよ。


