 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式5 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次方程式$x^2+ax+b=0$の2つの解に、それぞれ1を加えた数を解に持つ2次方程式が$x^2+bx+aー6=0$であるという。定数a、bを求めよ。
2次方程式$x^2-px+2=0$の2つの解の和と積を2つの解に持つ2次方程式が$x^2-5x+q=0$であるという。定数a、bの値を求めよ。
Aさんは2次方程式の定数項を違えたために$x=-3±\sqrt{14}$ という解を導き、Bさんは同じ2次方程式の1次の項の係数を読み違えたために、x=1、5という解を導いた。もとの正しい2次方程式の解を求めよ。
この動画を見る
2次方程式$x^2+ax+b=0$の2つの解に、それぞれ1を加えた数を解に持つ2次方程式が$x^2+bx+aー6=0$であるという。定数a、bを求めよ。
2次方程式$x^2-px+2=0$の2つの解の和と積を2つの解に持つ2次方程式が$x^2-5x+q=0$であるという。定数a、bの値を求めよ。
Aさんは2次方程式の定数項を違えたために$x=-3±\sqrt{14}$ という解を導き、Bさんは同じ2次方程式の1次の項の係数を読み違えたために、x=1、5という解を導いた。もとの正しい2次方程式の解を求めよ。
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式4 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
pを実数とする。次の2次方程式の解の1つが[ ]内の数であるとき、他の解を求めよ。また、定数pの値を求めよ。
(1) $2x^2+10x+p=0$ $[\displaystyle \frac{1}{2}
] $
(2)$x^2+px+4=0$ $[1+\sqrt{3}i]$
2次方程式$x^2-2x+7=0$の2つの解をα,βとするとき、次の2数を解とする2次方程式を作れ。
(1) α+2,β+2
(2) -2α, -2β
(3) α², β²
2次方程式$x^2-5x+5=0$は異なる2つの実数解をもつ。2つの実数解の小数部分を解とする2次方程式を作れ。
この動画を見る
pを実数とする。次の2次方程式の解の1つが[ ]内の数であるとき、他の解を求めよ。また、定数pの値を求めよ。
(1) $2x^2+10x+p=0$ $[\displaystyle \frac{1}{2}
] $
(2)$x^2+px+4=0$ $[1+\sqrt{3}i]$
2次方程式$x^2-2x+7=0$の2つの解をα,βとするとき、次の2数を解とする2次方程式を作れ。
(1) α+2,β+2
(2) -2α, -2β
(3) α², β²
2次方程式$x^2-5x+5=0$は異なる2つの実数解をもつ。2つの実数解の小数部分を解とする2次方程式を作れ。
【受験算数】ニュートン算 行列がなくなる2【問題文は概要欄】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるスタジアムの入場口に、入場開始時刻に3000人の行列ができています。この 行列には、1分に30人の割合で後から並ぶ人がきます。入場ゲートが1か所だと、 入場開始から行列がなくなるまで75分かかります。入場開始から5分で行列がなく なるようにするには、入場ゲートを何か所にすればよいですか。
この動画を見る
あるスタジアムの入場口に、入場開始時刻に3000人の行列ができています。この 行列には、1分に30人の割合で後から並ぶ人がきます。入場ゲートが1か所だと、 入場開始から行列がなくなるまで75分かかります。入場開始から5分で行列がなく なるようにするには、入場ゲートを何か所にすればよいですか。
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式3 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a、b、cは実数の定数とする。2次方程式ax²+bx+c=0は次の場合において、虚数解をもたないことを示せ。
(1) b=a+c
(2)a+c=0
(3)aとcが異符号
次の2次方程式の解の種類を判別せよ。ただし、a、bは実数の定数とする。
13x²-2(2a-3b)x+a²+b²=0
この動画を見る
a、b、cは実数の定数とする。2次方程式ax²+bx+c=0は次の場合において、虚数解をもたないことを示せ。
(1) b=a+c
(2)a+c=0
(3)aとcが異符号
次の2次方程式の解の種類を判別せよ。ただし、a、bは実数の定数とする。
13x²-2(2a-3b)x+a²+b²=0
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式2 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
この動画を見る
2つの2次方程式x²+mx+m=0, x²+mx+1=0がともに虚数解をもつとき、定数mの値の範囲を定めよ。
2つの2次方程式x²+2mx-2m=0, x²+(m-1)x+m²=0が次の条件を満たすとき、定数mの値の範囲を定めよ。
(1)少なくとも一方が実数解をもつ
(2)一方だけが実数解をもつ
【数Ⅱ】【複素数と方程式】2次方程式の解と判別式1 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2次方程式を解け。
(1)$3(x+1)^2-2(x+1)-1=0$
(2)$2(x-1)^2-4(x-1)+3=0$
(3)$x^2-\sqrt{2} x+\sqrt{2} -1=0$
(4)$x^2-2x+9+2\sqrt{15}=0$
kは定数とする。次の方程式の解の種類を判別せよ。
(1)$kx^2-3x+1=0$
(2)$(k^2-1) x^2+2(k-1)+2=0$
この動画を見る
次の2次方程式を解け。
(1)$3(x+1)^2-2(x+1)-1=0$
(2)$2(x-1)^2-4(x-1)+3=0$
(3)$x^2-\sqrt{2} x+\sqrt{2} -1=0$
(4)$x^2-2x+9+2\sqrt{15}=0$
kは定数とする。次の方程式の解の種類を判別せよ。
(1)$kx^2-3x+1=0$
(2)$(k^2-1) x^2+2(k-1)+2=0$
【数Ⅱ】【複素数と方程式】複素数の純虚数、共役 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
この動画を見る
2つの複素数a+biと2-3iの和が純虚数、積が実数となるように、実数a, bの値を定めよ。
虚数α、βの和、積がともに実数ならば、α、βは互いに共役であることを示せ。
【数Ⅱ】【複素数と方程式】複素数基本 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
この動画を見る
(1)$\left({\displaystyle \frac{3-2i}{2+3i}}\right)^2$
(2)$\left({\displaystyle \frac{-1+\sqrt{3}i}{2}}\right)^2$
(3)$(2+i)^3+(2-i)^3$
(4)$\left(\displaystyle \frac{1}{i}-i\right)\left(\displaystyle \frac{2}{i}+i\right)i^3$
(5)$\displaystyle \frac{2+3i}{3-2i}+\displaystyle \frac{2-3i}{3+2i}$
(6)$\displaystyle \frac{1}{i}+1-i+i²-i³+i⁴$
$x=\displaystyle \frac{-1+\sqrt{5}i}{2}$,$y=\displaystyle \frac{-1-\sqrt{5}i}{2}$であるとき、次の式の値を求めよ。
(1)$x+y$
(2)$xy$
(3)$x^2+y^2$
(4)$x^3+y^3+x^2y+xy^2$
次の等式を満たす実数x,yの値を求めよ。
(1)$(2i+3)x+(2-3i)y=5-i$
(2)$(1-2i)(x+yi)=2+6i$
(3)$(1+xi)^2+(x+i)^2=0$
(4)$\displaystyle \frac{1}{2+i}+\displaystyle \frac{1}{x+yi}=\displaystyle \frac{1}{2}$
【数A】【整数の性質】n進法 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の数を[ ]内の表し方で表せ。
(1)1100101(2) [3進法]
(2)12121(3) [2進法]
(3)1234(5) [2進法]
nは2以上の自然数とする。10進法の数72をn進法で表すと132(n)となる。nを求めよ。
次の個数を10進法の数で答えよ。
(1)2進法で表したとき,6桁(この6は10進法の数)となるような数
(2)5進法で表したとき,4桁(この4は10進法の数)となるような数
この動画を見る
次の数を[ ]内の表し方で表せ。
(1)1100101(2) [3進法]
(2)12121(3) [2進法]
(3)1234(5) [2進法]
nは2以上の自然数とする。10進法の数72をn進法で表すと132(n)となる。nを求めよ。
次の個数を10進法の数で答えよ。
(1)2進法で表したとき,6桁(この6は10進法の数)となるような数
(2)5進法で表したとき,4桁(この4は10進法の数)となるような数
【高校物理】平面運動の相対速度【毎週土曜日16時更新!】

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
水平な直線状のレールを、速さ5.0m/sで走っている電車内の人が、地面に対して鉛直下向きに降る雨を見る。このとき、雨滴は、鈴直方向と30°の角をなして落下しているように見えた。地面に対する雨滴の落下の速さを求めよ。
この動画を見る
水平な直線状のレールを、速さ5.0m/sで走っている電車内の人が、地面に対して鉛直下向きに降る雨を見る。このとき、雨滴は、鈴直方向と30°の角をなして落下しているように見えた。地面に対する雨滴の落下の速さを求めよ。
【高校化学】フェノールの製法【毎週土曜日16時更新!】

単元:
#化学#有機#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
フェノールの合成の流れを図に示す。(図は本編中)図中のA~Dにあてはまる化合物の構造と名称を答えよ。また、(1)の工業的製法の名称を答えよ。
この動画を見る
フェノールの合成の流れを図に示す。(図は本編中)図中のA~Dにあてはまる化合物の構造と名称を答えよ。また、(1)の工業的製法の名称を答えよ。
【受験算数】ニュートン算 行列がなくなる【問題文は概要欄】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるスタジアムの入場口に、入場開始時刻に2000人の行列ができています。この 行列には、1分に40人の割合で後から並ぶ人がきます。入場ゲートが1か所だと、 入場開始から行列がなくなるまで25分かかります。入場ゲートが7か所だと、入場開始から行列がなくなるまで何分何秒かかりますか。
この動画を見る
あるスタジアムの入場口に、入場開始時刻に2000人の行列ができています。この 行列には、1分に40人の割合で後から並ぶ人がきます。入場ゲートが1か所だと、 入場開始から行列がなくなるまで25分かかります。入場ゲートが7か所だと、入場開始から行列がなくなるまで何分何秒かかりますか。
【数A】【整数の性質】合同式 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものを求めよ。
(1)$37^{100}$を6で割った余り
(2$)5^{80}$を8で割った余り
(3)$3^{100}$を13で割った余り
(4)$4^{200}$を9で割った余り
nを整数とする。合同式を用いて、次のものを求めよ。
(1)nを8で割った余りが3であるとき、n²+2n+5を8で割った余り
(2)nを17で割った余りが15であるとき、3n²+5n+9を17で割った余り
(3)nを35で割った余りが2であるとき、n⁴+3n³+4を35で割った余り
(4)nを41で割った余りが38であるとき、n³+7n²+8を41で割った余り
合同式を用いて、次のものを求めよ。
(1)$123^{122}$の一の位
(2)$7^{251}$の下2桁
この動画を見る
次のものを求めよ。
(1)$37^{100}$を6で割った余り
(2$)5^{80}$を8で割った余り
(3)$3^{100}$を13で割った余り
(4)$4^{200}$を9で割った余り
nを整数とする。合同式を用いて、次のものを求めよ。
(1)nを8で割った余りが3であるとき、n²+2n+5を8で割った余り
(2)nを17で割った余りが15であるとき、3n²+5n+9を17で割った余り
(3)nを35で割った余りが2であるとき、n⁴+3n³+4を35で割った余り
(4)nを41で割った余りが38であるとき、n³+7n²+8を41で割った余り
合同式を用いて、次のものを求めよ。
(1)$123^{122}$の一の位
(2)$7^{251}$の下2桁
【数A】【整数の性質】座標の考え方 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
平らな広場の地点Oを原点として,東の方向をx軸の正の向き,北の方向をy軸の正の向きとする座標平面を考える。また,1mを1の長さとする。
地点A,Bの座標をそれぞれ(-4,1),(3,-5)とする。
(1)地点Aから東に5m進み,南に7m進んだ位置にある点の座標を答えよ。
(2)地点Bから西に4m進み,北に1m進んだ位置にある点の座標を答えよ。
平らな広場の地点Oを原点として,東の方向をx軸の正の向き,北の方向をy軸の正の向き,真上の方向をz軸の正の向きとする座標空間を考える。また,1mを1の長さとする。この広場の上空に気球Pが浮かんでいる。レーザー距離計で,次のように測定した。ただし,気球Pは1つの点とみなす。
[1]地点Oから東へ15m,北へ1m進んだ地点A(15,1,0)から,Pまでの距離を測ると41m
[2]地点Oから北へ21m進んだ地点B(0,21,0)から,Pまでの距離を測ると56m
[3]地点Oから南へ11m進んだ地点C(0,-11,0)から,Pまでの距離を測ると56m
このとき,気球Pの位置を求めよ。
座標空間において,A(3,2,0),B(3,4,-2),C(1,2,-2)を頂点とする三角形は,正三角形であることを示せ。
この動画を見る
平らな広場の地点Oを原点として,東の方向をx軸の正の向き,北の方向をy軸の正の向きとする座標平面を考える。また,1mを1の長さとする。
地点A,Bの座標をそれぞれ(-4,1),(3,-5)とする。
(1)地点Aから東に5m進み,南に7m進んだ位置にある点の座標を答えよ。
(2)地点Bから西に4m進み,北に1m進んだ位置にある点の座標を答えよ。
平らな広場の地点Oを原点として,東の方向をx軸の正の向き,北の方向をy軸の正の向き,真上の方向をz軸の正の向きとする座標空間を考える。また,1mを1の長さとする。この広場の上空に気球Pが浮かんでいる。レーザー距離計で,次のように測定した。ただし,気球Pは1つの点とみなす。
[1]地点Oから東へ15m,北へ1m進んだ地点A(15,1,0)から,Pまでの距離を測ると41m
[2]地点Oから北へ21m進んだ地点B(0,21,0)から,Pまでの距離を測ると56m
[3]地点Oから南へ11m進んだ地点C(0,-11,0)から,Pまでの距離を測ると56m
このとき,気球Pの位置を求めよ。
座標空間において,A(3,2,0),B(3,4,-2),C(1,2,-2)を頂点とする三角形は,正三角形であることを示せ。
【数A】【整数の性質】進数応用 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3桁の自然数Nを7進法で表すと3桁の数a0b(7)となり,5進法で表すと逆の並びの3桁の数b0a(5)となるという。a,bを求めよ。また,Nを10進法で表せ。
自然数Nを5進法と7進法で表すと,それぞれ3桁の数abc(5),cab(7)になるという。a,b,cを求めよ。また,Nを10進法で表せ。
5種類の数字0,1,2,3,4を用いて表される自然数を,次のように小さい方から順に並べる。
1,2,3,4,10,11,12,13,14,20,21,22,……
(1) 2020番目の数をいえ。
(2) 2020は何番目の数か。
この動画を見る
3桁の自然数Nを7進法で表すと3桁の数a0b(7)となり,5進法で表すと逆の並びの3桁の数b0a(5)となるという。a,bを求めよ。また,Nを10進法で表せ。
自然数Nを5進法と7進法で表すと,それぞれ3桁の数abc(5),cab(7)になるという。a,b,cを求めよ。また,Nを10進法で表せ。
5種類の数字0,1,2,3,4を用いて表される自然数を,次のように小さい方から順に並べる。
1,2,3,4,10,11,12,13,14,20,21,22,……
(1) 2020番目の数をいえ。
(2) 2020は何番目の数か。
【数A】【整数の性質】ユークリッドの互除法の利用 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)3で割ると1余り,7で割ると3余るような自然数のうち,3桁で最大のものと最小のものを求めよ。
(2)8で割ると4余り,13で割ると9余るような自然数のうち,4桁で最大のものと最小のものを求めよ。
次の等式を満たす自然数x,yの組をすべて求めよ。
(1)7x+2y=41
(2)3x+4y=36
(3)4x+5y=100
所持金660円で1個50円の商品Aと1個80円の商品Bを買う。所持金をちょうど使い切るとき,商品Aと商品Bをそれぞれ何個買えばよいか。ただし,消費税は考えないものとする。
この動画を見る
(1)3で割ると1余り,7で割ると3余るような自然数のうち,3桁で最大のものと最小のものを求めよ。
(2)8で割ると4余り,13で割ると9余るような自然数のうち,4桁で最大のものと最小のものを求めよ。
次の等式を満たす自然数x,yの組をすべて求めよ。
(1)7x+2y=41
(2)3x+4y=36
(3)4x+5y=100
所持金660円で1個50円の商品Aと1個80円の商品Bを買う。所持金をちょうど使い切るとき,商品Aと商品Bをそれぞれ何個買えばよいか。ただし,消費税は考えないものとする。
【数A】【整数の性質】ユークリッドの互除法最大公約数を考える問題 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす自然数nをすべて求めよ。
(1)14n+52と4n+17の最大公約数が5になるような50以下のn
(2)11n+39と6n+20の最大公約数が7になるような100以下のn
nは自然数とする。n²+7n+36とn+5の最大公約数として考えられる数をすべて求めよ。
この動画を見る
次の条件を満たす自然数nをすべて求めよ。
(1)14n+52と4n+17の最大公約数が5になるような50以下のn
(2)11n+39と6n+20の最大公約数が7になるような100以下のn
nは自然数とする。n²+7n+36とn+5の最大公約数として考えられる数をすべて求めよ。
【数A】【整数の性質】ユークリッドの互除法図形を用いる問題 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
縦の長さが864,横の長さが1357である長方形において,長方形をできるだけ大きい正方形で切り取れるだけ切り取る。残った部分の長方形も同様に,その長方形をできるだけ大きい正方形で切り取れるだけ切り取る。この作業を,最初の長方形がすべて正方形で切り取られるまで繰り返す。
(1)最初に切り取られる正方形の1辺の長さを求めよ。また,残った部分の短辺の長さを求めよ。
(2)切り取られた正方形のうち,最も小さい正方形の面積を求めよ。
(3)切り取られた正方形は何種類か。
(4)切り取られた正方形の個数を求めよ。
縦の長さが1,横の長さが$\sqrt{3}$である長方形ABCDにおいて,長方形をできるだけ大きい正方形で切り取れるだけ切り取る。残った部分の長方形も同様に,その長方形をできるだけ大きい正方形で切り取れるだけ切り取る。右の図はこの作業を何回か繰り返したときの図である。この図の中にある長方形で,長方形ABCDと相似である長方形を見つけ,それを用いて$\sqrt{3}$が無理数であることを証明せよ。
この動画を見る
縦の長さが864,横の長さが1357である長方形において,長方形をできるだけ大きい正方形で切り取れるだけ切り取る。残った部分の長方形も同様に,その長方形をできるだけ大きい正方形で切り取れるだけ切り取る。この作業を,最初の長方形がすべて正方形で切り取られるまで繰り返す。
(1)最初に切り取られる正方形の1辺の長さを求めよ。また,残った部分の短辺の長さを求めよ。
(2)切り取られた正方形のうち,最も小さい正方形の面積を求めよ。
(3)切り取られた正方形は何種類か。
(4)切り取られた正方形の個数を求めよ。
縦の長さが1,横の長さが$\sqrt{3}$である長方形ABCDにおいて,長方形をできるだけ大きい正方形で切り取れるだけ切り取る。残った部分の長方形も同様に,その長方形をできるだけ大きい正方形で切り取れるだけ切り取る。右の図はこの作業を何回か繰り返したときの図である。この図の中にある長方形で,長方形ABCDと相似である長方形を見つけ,それを用いて$\sqrt{3}$が無理数であることを証明せよ。
【数A】【整数の性質】素因数分解、素数について ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは自然数とする。2310/nが素数となるnは何個あるか。
nは自然数とする。n²-14n+40が素数となるようなnをすべて求めよ。
次の問いに答えよ。
(1)(ア)5以上の素数を小さい方から順に10個あげよ。
(イ)(ア)であげた素数から予想できることについて,下の文章の□に当てはまる自然数のうち,最大のものを求めよ。ただし,□には同じ自然数が入るものとする。
5以上の素数は,□の倍数から1引いた数か,□の倍数に1足した数である。
(2)(1)(イ)の予想が正しいことを証明せよ。
この動画を見る
nは自然数とする。2310/nが素数となるnは何個あるか。
nは自然数とする。n²-14n+40が素数となるようなnをすべて求めよ。
次の問いに答えよ。
(1)(ア)5以上の素数を小さい方から順に10個あげよ。
(イ)(ア)であげた素数から予想できることについて,下の文章の□に当てはまる自然数のうち,最大のものを求めよ。ただし,□には同じ自然数が入るものとする。
5以上の素数は,□の倍数から1引いた数か,□の倍数に1足した数である。
(2)(1)(イ)の予想が正しいことを証明せよ。
【受験算数】ニュートン算の基本 入れる・出す・減る【問題文は概要欄】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(1)~(4)の□にあてはまる数を答えなさい。
(1) 給水管と排水管がついている水そうがあり、1200Lの水が入っています。いま。 給水管からは毎分15L.排水管からは毎分40Lの水を流します。水そうが空 になるのは□分後です。
(2) 給水管と排水管がついている水そうがあり、□Lの水が入っています。給 水管からは毎分20L、排水管からは毎分50Lの水を流すと、水そうが空にな るのは15分後です。
(3) 給水管と排水管がついている水そうがあり、120Lの水が入っています。給水管からは毎分□L、排水管からは毎分25Lの水を流すと、水そうが空にな るのは10分後です。
(4) 給水管と排水管がついている水そうがあり、1920Lの水が入っています。給 水管からは毎分2L、排水管からは毎分□Lの水を流すと、水そうが空に なるのは40分後です。
この動画を見る
次の(1)~(4)の□にあてはまる数を答えなさい。
(1) 給水管と排水管がついている水そうがあり、1200Lの水が入っています。いま。 給水管からは毎分15L.排水管からは毎分40Lの水を流します。水そうが空 になるのは□分後です。
(2) 給水管と排水管がついている水そうがあり、□Lの水が入っています。給 水管からは毎分20L、排水管からは毎分50Lの水を流すと、水そうが空にな るのは15分後です。
(3) 給水管と排水管がついている水そうがあり、120Lの水が入っています。給水管からは毎分□L、排水管からは毎分25Lの水を流すと、水そうが空にな るのは10分後です。
(4) 給水管と排水管がついている水そうがあり、1920Lの水が入っています。給 水管からは毎分2L、排水管からは毎分□Lの水を流すと、水そうが空に なるのは40分後です。
【数A】【整数の性質】素因数分解を利用する問題 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような自然数の個数を求めよ。
(1)108以下の自然数で,108と互いに素である自然数
(2)600以下の自然数で,600と互いに素である自然数
(1)1から240までの240個の自然数の積N=1・2・3・・・240について,Nを素因数分解したとき,素因数3の個数を求めよ。
(2)1から450までの450個の自然数の積N=1・2・3・・・450について,Nを素因数分解したとき,素因数7の個数を求めよ。
次のような自然数の積Nを計算すると,末尾には0が連続して何個並ぶか
(1)1から125までの125個の自然数の積N=1・2・3・・・125
(2)1から300までの300個の自然数の積N=1・2・3・・・300
この動画を見る
次のような自然数の個数を求めよ。
(1)108以下の自然数で,108と互いに素である自然数
(2)600以下の自然数で,600と互いに素である自然数
(1)1から240までの240個の自然数の積N=1・2・3・・・240について,Nを素因数分解したとき,素因数3の個数を求めよ。
(2)1から450までの450個の自然数の積N=1・2・3・・・450について,Nを素因数分解したとき,素因数7の個数を求めよ。
次のような自然数の積Nを計算すると,末尾には0が連続して何個並ぶか
(1)1から125までの125個の自然数の積N=1・2・3・・・125
(2)1から300までの300個の自然数の積N=1・2・3・・・300
【数A】【整数の性質】最小公倍数、最大公約数の基本2 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
みかんが435個,りんごが268個ある。何人かの子どもに,みかんもりんごも平等に,できるだけ多く配ったところ,みかんは45個,りんごは34個余った。子どもの人数を求めよ。
(1)nは自然数で,n/20,n/42がともに自然数となるという。このようなnのうちで最も小さいものを求めよ。
(2)42/5, 21/10, 35/16,のいずれに掛けても積が自然数となる分数のうち,最も小さいものを求めよ。
この動画を見る
みかんが435個,りんごが268個ある。何人かの子どもに,みかんもりんごも平等に,できるだけ多く配ったところ,みかんは45個,りんごは34個余った。子どもの人数を求めよ。
(1)nは自然数で,n/20,n/42がともに自然数となるという。このようなnのうちで最も小さいものを求めよ。
(2)42/5, 21/10, 35/16,のいずれに掛けても積が自然数となる分数のうち,最も小さいものを求めよ。
【数A】【整数の性質】最小公倍数、最大公約数の基本1 ※問題文は概要欄

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#整数の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
この動画を見る
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
【受験算数】平面図形:合同な図形を探す 【洛南高附中2019】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#洛南高校附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
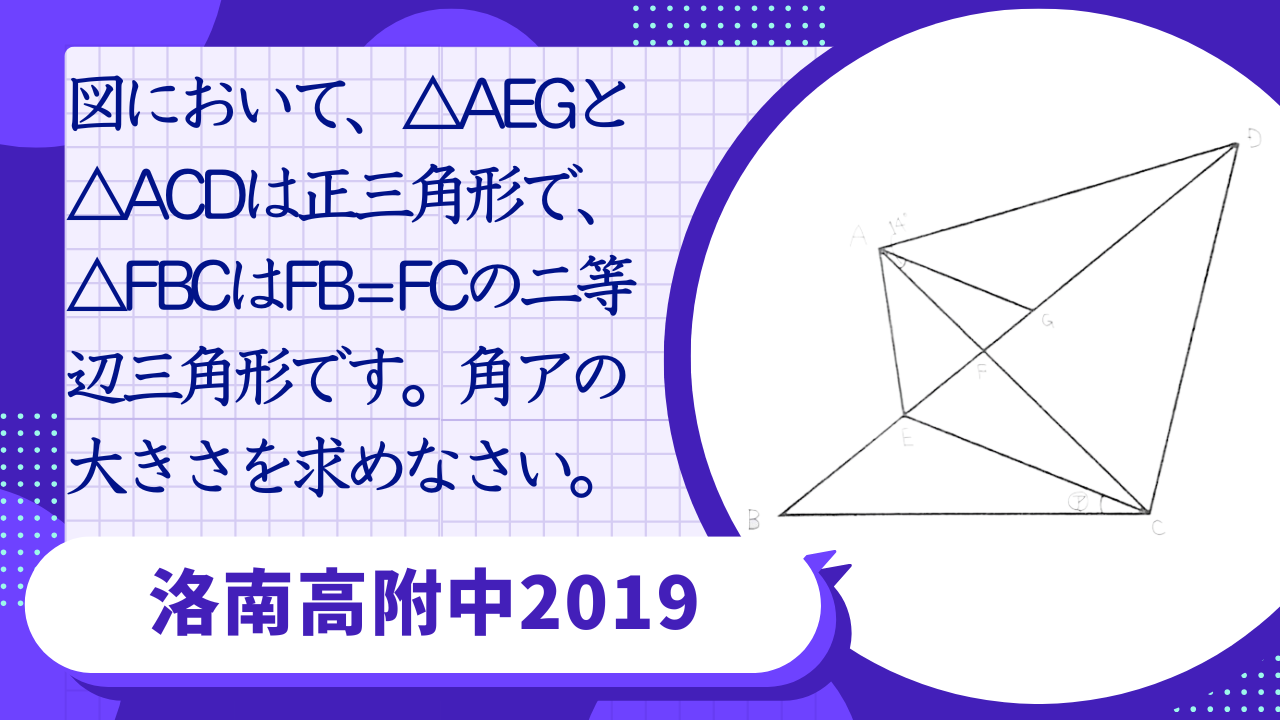
図において、△AEGと△ACDは正三角形で、△FBCはFB=FCの二等辺三角形です。角アの大きさを求めなさい。
この動画を見る
図において、△AEGと△ACDは正三角形で、△FBCはFB=FCの二等辺三角形です。角アの大きさを求めなさい。
【受験算数】平面図形:折り返した図形 【大阪星光中2020】

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#大阪星光学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、長方形の紙テープを2回折りました。角アの大きさを求めなさい。
この動画を見る
図のように、長方形の紙テープを2回折りました。角アの大きさを求めなさい。
【数Ⅲ】【微分とその応用】不等式の応用6 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。次の方程式の異なる実数解の個数を求めよ。
(2)では、必要ならば$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{e^x} =0$を用いてよい。
(1) $x^3-ax+2a$=0
(2) $2x-1=ae^{ -x }$
この動画を見る
aは定数とする。次の方程式の異なる実数解の個数を求めよ。
(2)では、必要ならば$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{e^x} =0$を用いてよい。
(1) $x^3-ax+2a$=0
(2) $2x-1=ae^{ -x }$
【数Ⅲ】【微分とその応用】不等式の応用5 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のことが成り立つことを証明せよ。
$0≦x≦1$のとき
$1-x+x²e^x≦e^x≦1+x+\displaystyle \frac{1}{2}
x²e^x$
この動画を見る
次のことが成り立つことを証明せよ。
$0≦x≦1$のとき
$1-x+x²e^x≦e^x≦1+x+\displaystyle \frac{1}{2}
x²e^x$
【数Ⅲ】【微分とその応用】不等式の応用4 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x→∞$のとき、$y=x$が$y=\log x$と比較して、
より急速に増大すること、すなわち
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{\log x} =\infty$
が成り立つことを証明せよ。
ただし、まずは次の①~③のどれか1つを証明し、それを利用せよ。
①$x≧4$のとき、$x^2>\log x$が成り立つ
②$x≧4$のとき、$x>\log x$が成り立つ
③$x≧4$のとき、$\sqrt{x}>\log x$が成り立つ
この動画を見る
$x→∞$のとき、$y=x$が$y=\log x$と比較して、
より急速に増大すること、すなわち
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x}{\log x} =\infty$
が成り立つことを証明せよ。
ただし、まずは次の①~③のどれか1つを証明し、それを利用せよ。
①$x≧4$のとき、$x^2>\log x$が成り立つ
②$x≧4$のとき、$x>\log x$が成り立つ
③$x≧4$のとき、$\sqrt{x}>\log x$が成り立つ
【数Ⅲ】【微分とその応用】不等式の応用3 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
すべての正の数xに対して、
不等式$\sqrt{x}>a\log x$が成り立つような定数aの値の範囲を求めよ。
この動画を見る
すべての正の数xに対して、
不等式$\sqrt{x}>a\log x$が成り立つような定数aの値の範囲を求めよ。
【数Ⅲ】【微分とその応用】不等式の応用2 ※問題文は概要欄

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のことが成り立つことを証明せよ。
(1) $b≧a>0$のとき $logb-loga≧\displaystyle \frac{2(b-a)}{(b+a)}$
(2) $0<α<β≦\displaystyle \frac{π}{2}$のとき $\displaystyle \frac{α}{β}<\displaystyle \frac{sin α}{sin β}$
この動画を見る
次のことが成り立つことを証明せよ。
(1) $b≧a>0$のとき $logb-loga≧\displaystyle \frac{2(b-a)}{(b+a)}$
(2) $0<α<β≦\displaystyle \frac{π}{2}$のとき $\displaystyle \frac{α}{β}<\displaystyle \frac{sin α}{sin β}$




