 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】平面図形:半円とおうぎ形【六甲学院中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#六甲学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
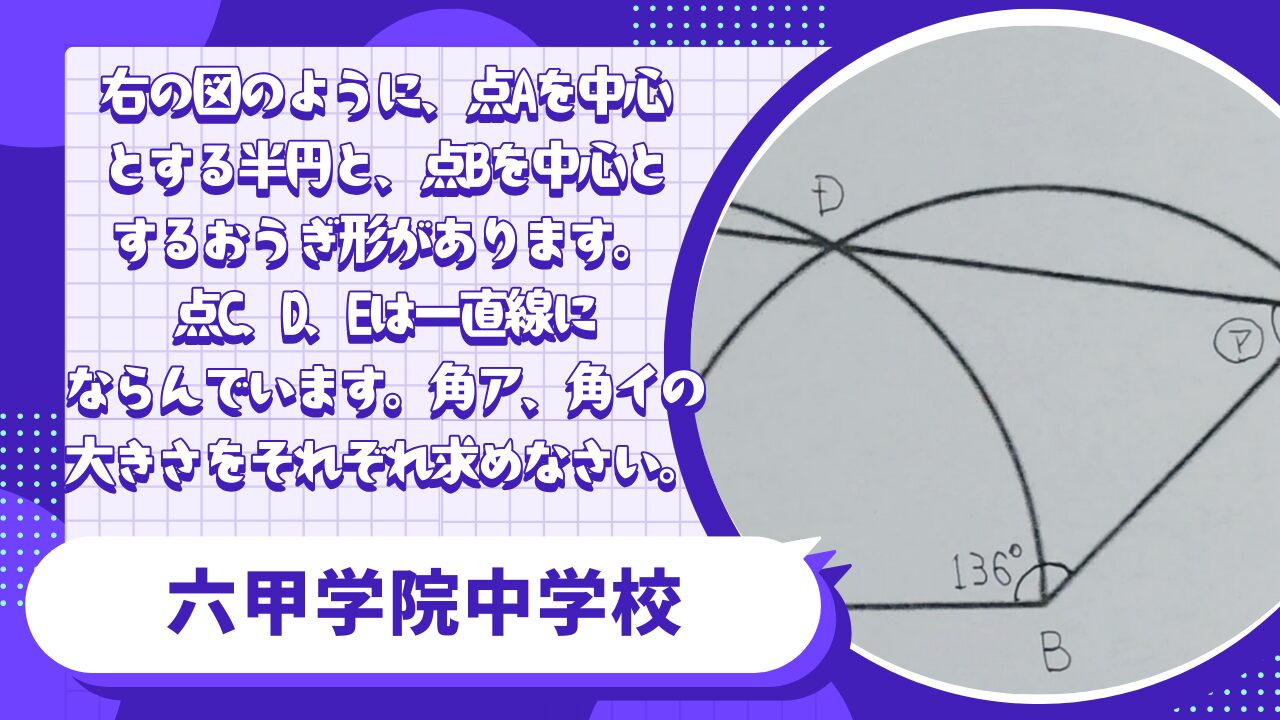
右の図のように、点Aを中心とする半円と、点Bを中心とするおう ぎ形があります。点C、D、Eは一直線にならんでいます。角ア、角イの大きさをそれぞれ求めなさい。
この動画を見る
右の図のように、点Aを中心とする半円と、点Bを中心とするおう ぎ形があります。点C、D、Eは一直線にならんでいます。角ア、角イの大きさをそれぞれ求めなさい。
複素数と方程式 数Ⅱ 剰余の定理と因数定理2【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
多項式P(x)を(x-1)(x+2)で割ると余りが3x-1である。P(x)をx-1およびx-2で割ったときの余りを、それぞれ求めよ。
多項式P(x)をx-2で割ると余りが5, x-3で割ると余りが9である。P(x)を(x-2)(x-3)で割ったときの余りを求めよ。
多項式P(x)をx²-3x+2で割ると余りが-x+4, x²-4x+3で割ると余りが3xである。P(x)をx²-5x+6で割ったときの余りを求めよ。
この動画を見る
多項式P(x)を(x-1)(x+2)で割ると余りが3x-1である。P(x)をx-1およびx-2で割ったときの余りを、それぞれ求めよ。
多項式P(x)をx-2で割ると余りが5, x-3で割ると余りが9である。P(x)を(x-2)(x-3)で割ったときの余りを求めよ。
多項式P(x)をx²-3x+2で割ると余りが-x+4, x²-4x+3で割ると余りが3xである。P(x)をx²-5x+6で割ったときの余りを求めよ。
複素数と方程式 数Ⅱ 剰余の定理と因数定理1【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の有理数の範囲で因数分解せよ。
(1) 4x³+x+1
(2) 2x³-x²+9
(3) 3x³+8x²-1
次の式を因数分解せよ。
(1) x⁴+5x³+5x²-5x-6
(2) x⁴+4x³-x²-16x-12
P(x)=x³+ax²+bx+cとする。P(x)はx²-1で割り切れ、また、P(x)をx-2で割ると余りが3である。このとき、定数a, b, cの値を求めよ。
この動画を見る
次の有理数の範囲で因数分解せよ。
(1) 4x³+x+1
(2) 2x³-x²+9
(3) 3x³+8x²-1
次の式を因数分解せよ。
(1) x⁴+5x³+5x²-5x-6
(2) x⁴+4x³-x²-16x-12
P(x)=x³+ax²+bx+cとする。P(x)はx²-1で割り切れ、また、P(x)をx-2で割ると余りが3である。このとき、定数a, b, cの値を求めよ。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円錐の側面の距離

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、底面の直径ABが6㎝、母線の長さが12㎝の円錐がある。母線OA上に点CをOC=4√2㎝となるようにとり、点Cから点Bまでの最短コースで結ぶとき、次の問いに答えなさい。
(1)この最短コースの長さを求めなさい。
(2)線分AC,弧AB、最短コースCBで囲まれる部分(図の斜線部分)の面積を求めなさい。
この動画を見る
右の図のように、底面の直径ABが6㎝、母線の長さが12㎝の円錐がある。母線OA上に点CをOC=4√2㎝となるようにとり、点Cから点Bまでの最短コースで結ぶとき、次の問いに答えなさい。
(1)この最短コースの長さを求めなさい。
(2)線分AC,弧AB、最短コースCBで囲まれる部分(図の斜線部分)の面積を求めなさい。
複素数と方程式 数Ⅱ 2次方程式の解と判別式6【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次方程式$x^2+ax+b=0$の2つの解に、それぞれ1を加えた数を解に持つ2次方程式が$x^2+bx+aー6=0$であるという。定数a、bを求めよ。
2次方程式$x^2-px+2=0$の2つの解の和と積を2つの解に持つ2次方程式が$x^2-5x+q=0$であるという。定数a、bの値を求めよ。
Aさんは2次方程式の定数項を違えたために$x=-3±\sqrt{14}$ という解を導き、Bさんは同じ2次方程式の1次の項の係数を読み違えたために、x=1、5という解を導いた。もとの正しい2次方程式の解を求めよ。
この動画を見る
2次方程式$x^2+ax+b=0$の2つの解に、それぞれ1を加えた数を解に持つ2次方程式が$x^2+bx+aー6=0$であるという。定数a、bを求めよ。
2次方程式$x^2-px+2=0$の2つの解の和と積を2つの解に持つ2次方程式が$x^2-5x+q=0$であるという。定数a、bの値を求めよ。
Aさんは2次方程式の定数項を違えたために$x=-3±\sqrt{14}$ という解を導き、Bさんは同じ2次方程式の1次の項の係数を読み違えたために、x=1、5という解を導いた。もとの正しい2次方程式の解を求めよ。
複素数と方程式 数Ⅱ 2次方程式の解と判別式5【ホーン・フィールドがていねいに解説】

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
pを実数とする。次の2次方程式の解の1つが[ ]内の数であるとき、他の解を求めよ。また、定数pの値を求めよ。
(1) $2x^2+10x+p=0$ $[\displaystyle \frac{1}{2}
] $
(2)$x^2+px+4=0$ $[1+\sqrt{3}i]$
2次方程式$x^2-2x+7=0$の2つの解をα,βとするとき、次の2数を解とする2次方程式を作れ。
(1) α+2,β+2
(2) -2α, -2β
(3) α², β²
2次方程式$x^2-5x+5=0$は異なる2つの実数解をもつ。2つの実数解の小数部分を解とする2次方程式を作れ。
この動画を見る
pを実数とする。次の2次方程式の解の1つが[ ]内の数であるとき、他の解を求めよ。また、定数pの値を求めよ。
(1) $2x^2+10x+p=0$ $[\displaystyle \frac{1}{2}
] $
(2)$x^2+px+4=0$ $[1+\sqrt{3}i]$
2次方程式$x^2-2x+7=0$の2つの解をα,βとするとき、次の2数を解とする2次方程式を作れ。
(1) α+2,β+2
(2) -2α, -2β
(3) α², β²
2次方程式$x^2-5x+5=0$は異なる2つの実数解をもつ。2つの実数解の小数部分を解とする2次方程式を作れ。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 柱の展開

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図は、辺ADと辺BCが平行で、AD=10㎝、BC=4㎝、AB=CD=5㎝の台形ABCDを底面とし、AE=BF=CG=DH=7cmを高さとする四角柱である。このとき、次の問いに答えなさい。
(1)この四角柱の側面上に、頂点Eから辺BFと辺CGに交わるように、頂点Dまで引く。このような線のうち、最も短い線の長さを求めなさい。
(2)平行な2つの線分AD,FGを含む平面でこの四角柱を切り、2つの立体に分けるとき、頂点Bを含む立体の体積を求めなさい。
この動画を見る
右の図は、辺ADと辺BCが平行で、AD=10㎝、BC=4㎝、AB=CD=5㎝の台形ABCDを底面とし、AE=BF=CG=DH=7cmを高さとする四角柱である。このとき、次の問いに答えなさい。
(1)この四角柱の側面上に、頂点Eから辺BFと辺CGに交わるように、頂点Dまで引く。このような線のうち、最も短い線の長さを求めなさい。
(2)平行な2つの線分AD,FGを含む平面でこの四角柱を切り、2つの立体に分けるとき、頂点Bを含む立体の体積を求めなさい。
確率分布と統計的推測 数B 推定1【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある町で、1つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者400人に対して行ったところ、政策支持者は216人であった。この町の有権者1万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95%の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度95%、信頼区間の幅4点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅2点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は15点としてよいことはわかっているものとする。
(1) 確率変数Zが標準正規分布に従うとき、P(|Z|≦◻︎)=0.99が成り立つ。◻︎に当てはまる最も適切な値を、次の①〜④のうちから1つ選べ。
①1.75 ②1.96 ③2.33 ④2.58
(2) ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度99%で推定せよ。
この動画を見る
ある町で、1つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者400人に対して行ったところ、政策支持者は216人であった。この町の有権者1万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95%の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度95%、信頼区間の幅4点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅2点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は15点としてよいことはわかっているものとする。
(1) 確率変数Zが標準正規分布に従うとき、P(|Z|≦◻︎)=0.99が成り立つ。◻︎に当てはまる最も適切な値を、次の①〜④のうちから1つ選べ。
①1.75 ②1.96 ③2.33 ④2.58
(2) ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度99%で推定せよ。
確率分布と統計的推測 数B 母集団分布【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本X1,X2を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均X(バー)の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出、非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、|X/n-1/2|≦0.01となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。100未満を切り上げて答えよ。
この動画を見る
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本X1,X2を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均X(バー)の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出、非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、|X/n-1/2|≦0.01となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。100未満を切り上げて答えよ。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円柱と四角錐
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
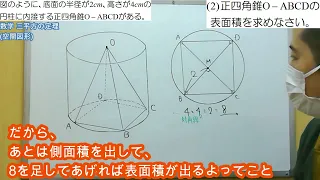
右の図のように、底面の半径が2cm、高さが4cmの円柱に内接する正四角錐O-ABCDがある。
(1)正四角錐O-ABCDの底面積を求めなさい。
(2)正四角錐O-ABCDの表面積を求めなさい。
この動画を見る
右の図のように、底面の半径が2cm、高さが4cmの円柱に内接する正四角錐O-ABCDがある。
(1)正四角錐O-ABCDの底面積を求めなさい。
(2)正四角錐O-ABCDの表面積を求めなさい。
【高校数学】数Ⅱ:微分法と積分法:定積分の計算(同じ積分範囲)【NI・SHI・NOがていねいに解説】

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
この動画を見る
次の定積分を求めよ。
$\displaystyle \int_{-2}^{3}(2x^2+4x-3)dx-2 \int_{-2}^{3}(x^2+4x+3)dx$
【受験算数】平面図形:正方形とおうぎ形【大妻中2021】

単元:
#算数(中学受験)#平面図形#角度と面積#大妻中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図1は、長方形、おうぎ形、半円が重なったものです。図2において、角アの大きさを求めなさい。
この動画を見る
右の図1は、長方形、おうぎ形、半円が重なったものです。図2において、角アの大きさを求めなさい。
指数対数 数Ⅱ 対数関数グラフ、方程式、不等式【ゆう☆たろうがていねいに解説】

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#指数関数と対数関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。
(1)$y=log_2{(x-2)}$
(2)$y=log_{\frac{1}{3}}{x}+1$
(3)$y=log_{10}{(-x)}$
次の数の大小を不当号を用いて表せ。
(1)$log_{0.3}{4}$, $log_2{4}$, $log_3{4}$
(2)$log_{0.3}{0.5}$, $log_2{0.5}$, $log_3{0.5}$
(3)$log_4{9}$, $log_9{25}$, $1.5$
次の方程式を解け
(1)$log_{10}{(x+2)(x+5)}=1$
(2)$log_{\frac{1}{3}}{(9+x-x^2)}=-1$
次の方程式を解け
(1)$log_2{x}+log_2{(x+3)}=2$
(2)$log_4{(2x+3)}+log_4{(4x+1)}=2log_4{5}$
(3)$log_2{(3-x)}=log_4{(2x+18)}$
この動画を見る
次の関数のグラフをかけ。
(1)$y=log_2{(x-2)}$
(2)$y=log_{\frac{1}{3}}{x}+1$
(3)$y=log_{10}{(-x)}$
次の数の大小を不当号を用いて表せ。
(1)$log_{0.3}{4}$, $log_2{4}$, $log_3{4}$
(2)$log_{0.3}{0.5}$, $log_2{0.5}$, $log_3{0.5}$
(3)$log_4{9}$, $log_9{25}$, $1.5$
次の方程式を解け
(1)$log_{10}{(x+2)(x+5)}=1$
(2)$log_{\frac{1}{3}}{(9+x-x^2)}=-1$
次の方程式を解け
(1)$log_2{x}+log_2{(x+3)}=2$
(2)$log_4{(2x+3)}+log_4{(4x+1)}=2log_4{5}$
(3)$log_2{(3-x)}=log_4{(2x+18)}$
確率分布と統計的推測 数B 二項分布【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある植物の種子の発芽率は80%であるという。
この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900 個のうちn個以上の種子が発芽する確率が 80%以上となるようなnの最大値を求めよ。
この動画を見る
ある植物の種子の発芽率は80%であるという。
この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900 個のうちn個以上の種子が発芽する確率が 80%以上となるようなnの最大値を求めよ。
【数学】中高一貫校用問題集幾何:三平方の定理:空間図形 円錐と球

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、底面の半径が5㎝、高さが12㎝の円錐に、球Oが内接している。このとき、次の問いに答えなさい。
(1)球Oの半径を求めなさい。
(2)球Oが側面と接している部分の曲線の長さを求めなさい。
この動画を見る
右の図のように、底面の半径が5㎝、高さが12㎝の円錐に、球Oが内接している。このとき、次の問いに答えなさい。
(1)球Oの半径を求めなさい。
(2)球Oが側面と接している部分の曲線の長さを求めなさい。
【中学受験理科】豆電球の解き方2【毎週日曜日10時更新!】

単元:
#理科(中学受験)
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
直列並列が混同した複雑な電気回路の解き方を解説します。※回路図は動画内参照
この動画を見る
直列並列が混同した複雑な電気回路の解き方を解説します。※回路図は動画内参照
【数学】2023年度 第2回 全統高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問:小問集合
(1)$(3x-1)(9x^2+3x+1)$を展開せよ。
(2)$\displaystyle \frac{x-1}{1+\frac{1}{x+2}}$を簡単にせよ。
(3)2次関数$y=2x^2-x+1$の最小値を求めよ。
(4)iを虚数単位とする。$\displaystyle \frac{(2+i)^2}{i}$を$a+bi$(a,bは実数)の形で表せ。
(5)$AB=4,BC=\sqrt{7},CA=\sqrt{3}$である△ABCにおいて、cos∠BACの値と△ABCの面積を求めよ。
(6)a,a,b,b,c,cの6文字を1列に並べるとき、並べ方は全部で何通りか。このうち、a,aが隣り合わないような並べ方は何通りか。
第2問-i:2次不等式
aは正の定数とする。実数xについての2つの不等式 $ax^2+(2a-5)x-2a+1<0$・・・①、$│2x-3│≦3$・・・②がある。
(1)a=2のとき、①を解け。
(2)②を解け。
(3)②を満たすすべての実数xに対して、①が成り立つようなaの値の範囲を求めよ。
第2問-ii:図形と方程式
xy平面上に、2つの円$C₁:x^2+y^2-10x-a^2-4a+21=0、C2:x^2+y^2=5$がある。また、C₂上の点P(2,1)におけるC₂の 接線を$l$とする。ただし、aはa>-2を満たす定数とする。
(1)a=1のとき、C₁の中心の座標と半径を求めよ。
(2)$l$の方程式を求めよ。
(3)C₁と$l$が接するようなaの値を求めよ。また、このとき のC1と$l$の接点をQとするとき、線分PQの長さを求めよ。
第3問:複素数と方程式
a,bを実数の定数とする。xの3次式$ f(x)=x^3+(a+3)x^2+(3a+b)x+3b$ と、3次方程式 $f(x)=0$・・・(*)がある。
(1)f(-3)を求めよ。
(2)a=-1かつb=1のとき、(*)を解け。
(3)(*)が異なる2つの虚数解をもつためのa,bの条件を求めよ。
(4)a,bが(3)で求めた条件を満たすとし、(*)の異なる2つの虚数解をα,βとする。このとき、$α^2,β^2$がともに(*)の解となるようなa,bの値の組(a,b)をすべて求めよ。
第4問:確率
5枚のカード1,1,2,2,3が入った袋が1つあり、次の操作(I)を考える。
操作(I): 袋から2枚のカードを同時に取り出し、取り出した2枚のカードに書かれた数の和をXとし、取り出した2枚のカードを袋に戻す。
(1)操作(I)を1回行う。
(i)X=2となる確率を求めよ。
(ii)X=4となる確率を求めよ。
さらに、1枚の硬貨を用意し、操作(I)で定まるXの値に対して、次の操作(II)を考える。
操作(II):1枚の硬貨を投げ、表が出たらY=X+1とし、裏が出たらY=Xとする。
操作(I), (II)を(I), (II)の順に1回ずつ行うことを操作Tとする。
(2)操作Tを1回行う。
(i)Y=4となる確率を求めよ。
(ii)Yの期待値を求めよ。
(3)操作Tを3回繰り返すとき、3回のYの値の合計が15になる確率を求めよ。
第5問:三角関数
aを実数の定数とする。θの方程式$cos2θ+2(5a-1)sinθ-12a^2+6a-1=0$・・・(*)がある
(1)cos2θをsinθを用いて表せ。
(2)a=0とする。0≦θ<2πにおいて、(*)を解け。
(3)0≦θ<2πにおいて、(*)が異なる4個の解をもつとする。
(i)aのとり得る値の範囲を求めよ。
(ii)0≦θ<2πにおける(*)の4個の解を、小さい順にθ₁,θ₂,θ₃,θ₄とする。(θ₂-θ₁)+(θ₄-θ₃)=πとなるようなaの値を求めよ。
第6問:数列
nは自然数。等差数列{a_n}があり、a₁+a₂=8,a₄+a₅=20である。また、公比が実数である等比数列{b_n}があり、
b₁+b₂=4, b₄+b₅=108である。
(1)数列{a_n}の一般項を求めよ。また、数列{a_n}の初項から第n項までの和S_nを求めよ。
(2)数列{b_n}の一般項を求めよ。
(3)数列{c_n}は、左から順に次のような項が並べられた数列である。 b₁がa₁個、b₂がa₂個、b₃がa₃個、...、b_nがa_n個、... すなわち、{c}: b₁,...,b₁, b₂,...,b₂, b₃,..,b₃,...,b_n,...,b_n,...
(i)C₂₀₂₃の値を求めよ。ただし、結果は2¹⁰⁰のように指数表示のままでよい。
(ii)$\displaystyle \sum_{k=1}^{2023}c_k$の値を求めよ。ただし、結果は$2^{100}$のように指数表示のままでよい。
この動画を見る
第1問:小問集合
(1)$(3x-1)(9x^2+3x+1)$を展開せよ。
(2)$\displaystyle \frac{x-1}{1+\frac{1}{x+2}}$を簡単にせよ。
(3)2次関数$y=2x^2-x+1$の最小値を求めよ。
(4)iを虚数単位とする。$\displaystyle \frac{(2+i)^2}{i}$を$a+bi$(a,bは実数)の形で表せ。
(5)$AB=4,BC=\sqrt{7},CA=\sqrt{3}$である△ABCにおいて、cos∠BACの値と△ABCの面積を求めよ。
(6)a,a,b,b,c,cの6文字を1列に並べるとき、並べ方は全部で何通りか。このうち、a,aが隣り合わないような並べ方は何通りか。
第2問-i:2次不等式
aは正の定数とする。実数xについての2つの不等式 $ax^2+(2a-5)x-2a+1<0$・・・①、$│2x-3│≦3$・・・②がある。
(1)a=2のとき、①を解け。
(2)②を解け。
(3)②を満たすすべての実数xに対して、①が成り立つようなaの値の範囲を求めよ。
第2問-ii:図形と方程式
xy平面上に、2つの円$C₁:x^2+y^2-10x-a^2-4a+21=0、C2:x^2+y^2=5$がある。また、C₂上の点P(2,1)におけるC₂の 接線を$l$とする。ただし、aはa>-2を満たす定数とする。
(1)a=1のとき、C₁の中心の座標と半径を求めよ。
(2)$l$の方程式を求めよ。
(3)C₁と$l$が接するようなaの値を求めよ。また、このとき のC1と$l$の接点をQとするとき、線分PQの長さを求めよ。
第3問:複素数と方程式
a,bを実数の定数とする。xの3次式$ f(x)=x^3+(a+3)x^2+(3a+b)x+3b$ と、3次方程式 $f(x)=0$・・・(*)がある。
(1)f(-3)を求めよ。
(2)a=-1かつb=1のとき、(*)を解け。
(3)(*)が異なる2つの虚数解をもつためのa,bの条件を求めよ。
(4)a,bが(3)で求めた条件を満たすとし、(*)の異なる2つの虚数解をα,βとする。このとき、$α^2,β^2$がともに(*)の解となるようなa,bの値の組(a,b)をすべて求めよ。
第4問:確率
5枚のカード1,1,2,2,3が入った袋が1つあり、次の操作(I)を考える。
操作(I): 袋から2枚のカードを同時に取り出し、取り出した2枚のカードに書かれた数の和をXとし、取り出した2枚のカードを袋に戻す。
(1)操作(I)を1回行う。
(i)X=2となる確率を求めよ。
(ii)X=4となる確率を求めよ。
さらに、1枚の硬貨を用意し、操作(I)で定まるXの値に対して、次の操作(II)を考える。
操作(II):1枚の硬貨を投げ、表が出たらY=X+1とし、裏が出たらY=Xとする。
操作(I), (II)を(I), (II)の順に1回ずつ行うことを操作Tとする。
(2)操作Tを1回行う。
(i)Y=4となる確率を求めよ。
(ii)Yの期待値を求めよ。
(3)操作Tを3回繰り返すとき、3回のYの値の合計が15になる確率を求めよ。
第5問:三角関数
aを実数の定数とする。θの方程式$cos2θ+2(5a-1)sinθ-12a^2+6a-1=0$・・・(*)がある
(1)cos2θをsinθを用いて表せ。
(2)a=0とする。0≦θ<2πにおいて、(*)を解け。
(3)0≦θ<2πにおいて、(*)が異なる4個の解をもつとする。
(i)aのとり得る値の範囲を求めよ。
(ii)0≦θ<2πにおける(*)の4個の解を、小さい順にθ₁,θ₂,θ₃,θ₄とする。(θ₂-θ₁)+(θ₄-θ₃)=πとなるようなaの値を求めよ。
第6問:数列
nは自然数。等差数列{a_n}があり、a₁+a₂=8,a₄+a₅=20である。また、公比が実数である等比数列{b_n}があり、
b₁+b₂=4, b₄+b₅=108である。
(1)数列{a_n}の一般項を求めよ。また、数列{a_n}の初項から第n項までの和S_nを求めよ。
(2)数列{b_n}の一般項を求めよ。
(3)数列{c_n}は、左から順に次のような項が並べられた数列である。 b₁がa₁個、b₂がa₂個、b₃がa₃個、...、b_nがa_n個、... すなわち、{c}: b₁,...,b₁, b₂,...,b₂, b₃,..,b₃,...,b_n,...,b_n,...
(i)C₂₀₂₃の値を求めよ。ただし、結果は2¹⁰⁰のように指数表示のままでよい。
(ii)$\displaystyle \sum_{k=1}^{2023}c_k$の値を求めよ。ただし、結果は$2^{100}$のように指数表示のままでよい。
【高校物理】浮かぶ氷【毎週土曜日16時更新!】

単元:
#物理#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
密度ρ、体積Vの氷が、密度ρwの水に浮かんでいる。水中にある氷の体積をVw,重力加速度の大きさをgとして、次の各問に答えよ。 (1) 氷が受ける浮力の大きさを、Pw、Vw、gを用いて表せ。 (2) 氷の水面から出ている部分の体積を、V、ρ、ρwを用いて表せ。 (3)氷の密度がp=9.2✕10²、水の密度がPw=1.00x10³のとき、氷の水面から出ている部分の体積は、氷全体の体積の何%になるか。有効数字2桁で答えよ
この動画を見る
密度ρ、体積Vの氷が、密度ρwの水に浮かんでいる。水中にある氷の体積をVw,重力加速度の大きさをgとして、次の各問に答えよ。 (1) 氷が受ける浮力の大きさを、Pw、Vw、gを用いて表せ。 (2) 氷の水面から出ている部分の体積を、V、ρ、ρwを用いて表せ。 (3)氷の密度がp=9.2✕10²、水の密度がPw=1.00x10³のとき、氷の水面から出ている部分の体積は、氷全体の体積の何%になるか。有効数字2桁で答えよ
【受験算数】平面図形:二等辺三角形を作る【近畿大附中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#近畿大学附属中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
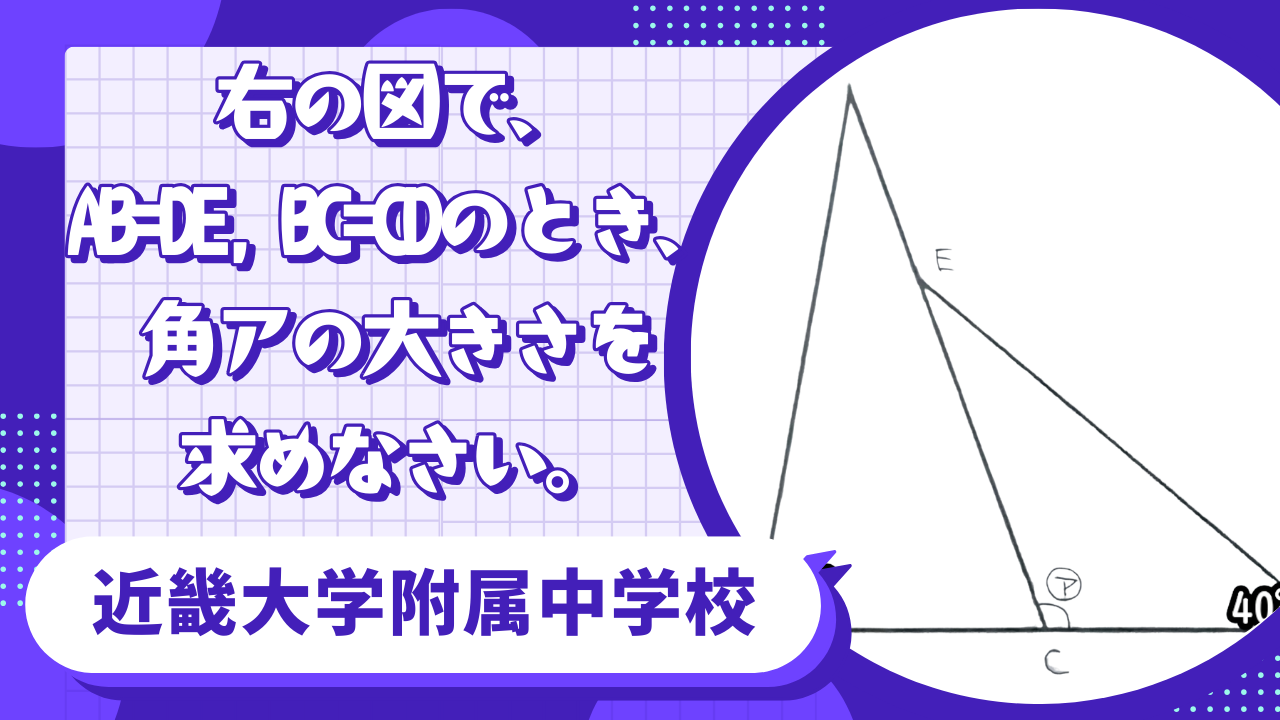
右の図で、AB=DE, BC=CDのとき、角アの大きさを求めなさい。
この動画を見る
右の図で、AB=DE, BC=CDのとき、角アの大きさを求めなさい。
確率分布と統計的推測 数B 正規分布6【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある2つの試験の結果は、平均点がそれぞれ57.6点、81.8点、標準偏差がそれぞれ10.3点、 5.7点であった。
Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。
どちらの試験を受けても、受験者全体としては優劣がないものとすると、 AとBはどちらが優れていると考えられるか。
ただし、得点は正規分布に従うものとする。
この動画を見る
ある2つの試験の結果は、平均点がそれぞれ57.6点、81.8点、標準偏差がそれぞれ10.3点、 5.7点であった。
Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。
どちらの試験を受けても、受験者全体としては優劣がないものとすると、 AとBはどちらが優れていると考えられるか。
ただし、得点は正規分布に従うものとする。
確率分布と統計的推測 数B 正規分布5【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある試験での成績の結果は、平均71点,標準偏差8点であった。 得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1)63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1) のとき、合格点を55点とすると、約何人が合格することになるか。
この動画を見る
ある試験での成績の結果は、平均71点,標準偏差8点であった。 得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1)63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1) のとき、合格点を55点とすると、約何人が合格することになるか。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 正四面体
単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
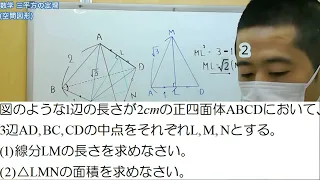
右の図のような1辺の長さが2㎝の正四面体ABCDにおいて、3辺AD,BC,CDの中点をそれぞれL,M,Nとする。
(1)線分LMの長さを求めなさい。
(2)△LMNの面積を求めなさい。
この動画を見る
右の図のような1辺の長さが2㎝の正四面体ABCDにおいて、3辺AD,BC,CDの中点をそれぞれL,M,Nとする。
(1)線分LMの長さを求めなさい。
(2)△LMNの面積を求めなさい。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 関数上の外接円の半径

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数y=-2x+4のグラフがx軸と交わる点をA,y軸と交わる点をBとする。Oを原点とするとき、△OABの外接円の半径を求めなさい。
この動画を見る
関数y=-2x+4のグラフがx軸と交わる点をA,y軸と交わる点をBとする。Oを原点とするとき、△OABの外接円の半径を求めなさい。
確率分布と統計的推測 数B 仮説検定【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
テニス選手A, Bの年間の対戦成績は、Aの23勝13敗であった。両選手の力に差があると判断してよいか。有意水準5%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下がったと判断してよいか。有意水準1%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下 がったと判断してよいか。有意水準1%で検定せよ。
この動画を見る
テニス選手A, Bの年間の対戦成績は、Aの23勝13敗であった。両選手の力に差があると判断してよいか。有意水準5%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下がったと判断してよいか。有意水準1%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下 がったと判断してよいか。有意水準1%で検定せよ。
確率分布と統計的推測 数B 正規分布4【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1000人の生徒に数学のテストをおこなったところ、その成績は平均48点、標準偏差15点であった。 成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の得点が78点以上である確率はいくらか?
(2)78点以上の生徒は約何人いると考えられるか。
(3)30点以下の生徒は約何人いると考えられるか。
この動画を見る
1000人の生徒に数学のテストをおこなったところ、その成績は平均48点、標準偏差15点であった。 成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の得点が78点以上である確率はいくらか?
(2)78点以上の生徒は約何人いると考えられるか。
(3)30点以下の生徒は約何人いると考えられるか。
【数学】中高一貫校用問題集幾何:三平方の定理:平面図形 放物線と直線の交点の面積

単元:
#数学(中学生)#中3数学#三平方の定理
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、放物線$y=\displaystyle \frac{x^2}{2}$と直線$y=\displaystyle \frac{x}{2}+6$が2点A, Bで交わっていて、原点O(0,0)から直線ABに引いた垂線をOHとする。
(1)△OABの面積を求めなさい。
(2)垂線OHの長さを求めなさい。
この動画を見る
右の図のように、放物線$y=\displaystyle \frac{x^2}{2}$と直線$y=\displaystyle \frac{x}{2}+6$が2点A, Bで交わっていて、原点O(0,0)から直線ABに引いた垂線をOHとする。
(1)△OABの面積を求めなさい。
(2)垂線OHの長さを求めなさい。
【高校数学】数Ⅲ:関数:逆関数と合成関数:逆関数の求め方とグラフの書き方【NI・SHI・NOがていねいに解説】

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の逆関数を求め,そのグラフをかけ。
$y=log_{\frac{1}{3}}x$
この動画を見る
次の関数の逆関数を求め,そのグラフをかけ。
$y=log_{\frac{1}{3}}x$
【受験算数】平面図形:二等辺三角形の利用【甲陽学院2021】

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#甲陽学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図で、角Aの大きさは24°で, AB, BC, CD, DE, EF, FG, GHの長さはすべて等しくなっています。角ア、角イの大きさをそれぞれ求めなさい。
この動画を見る
右の図で、角Aの大きさは24°で, AB, BC, CD, DE, EF, FG, GHの長さはすべて等しくなっています。角ア、角イの大きさをそれぞれ求めなさい。
確率分布と統計的推測 数B 正規分布3【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある県における高校2年生の男子の身長が、平均170.0cm、標準偏差値5.2cmの正規分布に従うものとする。
(1) 身長が 165 cm 以上の生徒は、約何%いるか。整数値で答えよ
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
この動画を見る
ある県における高校2年生の男子の身長が、平均170.0cm、標準偏差値5.2cmの正規分布に従うものとする。
(1) 身長が 165 cm 以上の生徒は、約何%いるか。整数値で答えよ
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
確率分布と統計的推測 数B 正規分布2【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N(m. σ²) に従う確率変数Xについて、Xの取る値を
m-1.5σ, m-0.5σ, m+0.5σ, m+1.5σ
によって、5つの階級に分けると、 各階級に何%ずつ含まれるか。
この動画を見る
正規分布N(m. σ²) に従う確率変数Xについて、Xの取る値を
m-1.5σ, m-0.5σ, m+0.5σ, m+1.5σ
によって、5つの階級に分けると、 各階級に何%ずつ含まれるか。




