 女子学院中学
女子学院中学
 女子学院中学
女子学院中学
2025年女子学院中学校 計算問題 #中学受験 #算数 #御三家

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学
指導講師:
重吉
問題文全文(内容文):
8と7/10+{(▭+1/4)×4.375+7/12}÷(1/6+1/9)=20.25
この動画を見る
8と7/10+{(▭+1/4)×4.375+7/12}÷(1/6+1/9)=20.25
円と角 女子学院中(改)
円と角 女子学院中(改)

2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
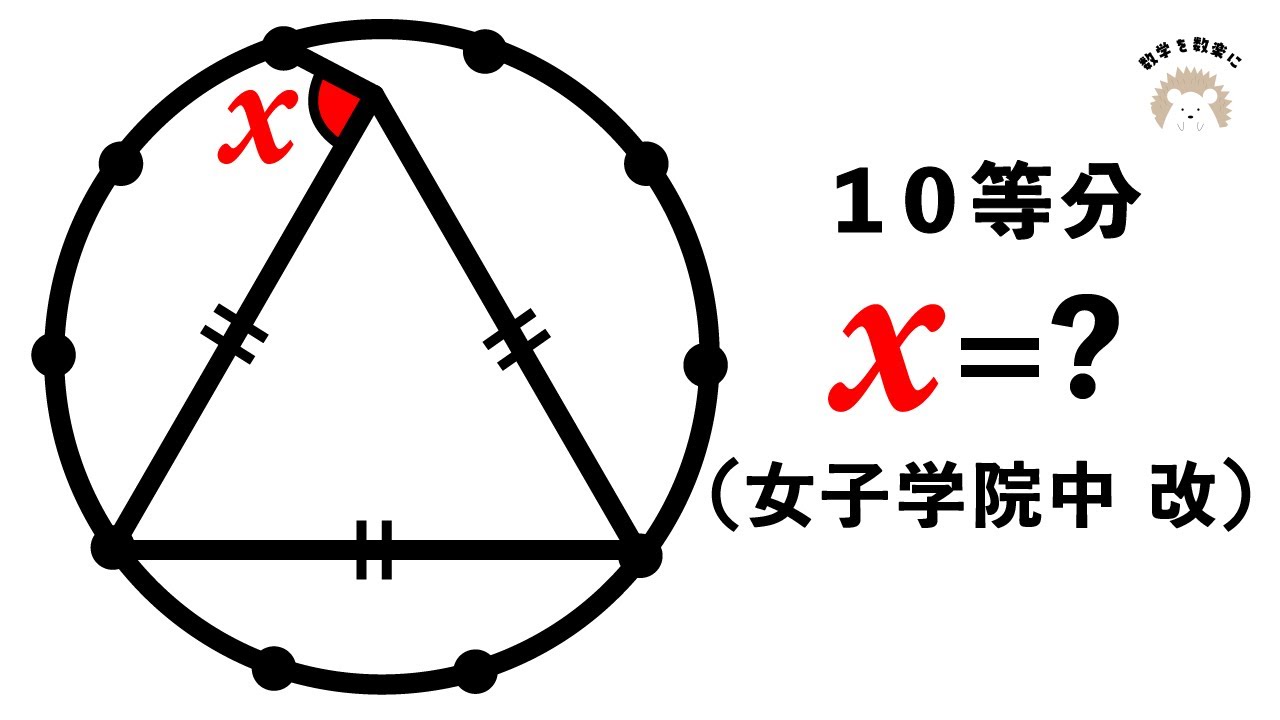
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
この動画を見る
1. にあてはまる数を入れなさい。
(1)18.7+ {13.4× (1/20 +▭) -2(1/3)} ÷2(6/11) =20.24
(2)図(動画内参照)のように、円周を10等分する点をとりました。
点0は円の中心、三角形ABCは正三角形です。
角㋐▭度、角㋑▭度、角㋒▭度
(3) 図(動画内参照)のように、長方形の紙を対角線を折り目として折りました。
斜線部の部分の面積は▭cm²です。
(4) 図(動画内参照)のように、棒を使って正三角形と正方形を作ります。
① 100個目の正方形を作り終えたとき、使った棒は▭本です。
② 棒が1000本あるとき、正三角形は▭個,正方形は▭個まで作ることができます。
(5) クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、 消しゴムは9個余りました。 I
クラスの人数は▭人,消しゴムは全部で▭個です。
2024年女子学院中算数大問①(1)~(5)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#女子学院中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
この動画を見る
※図は動画内参照
(1)
$\Box$に当てはまる数を入れなさい。
$18.7+\{ 13.4\times(\dfrac{1}{20}+\Box)-2\dfrac{1}{3} \}\div2\dfrac{6}{11}=20.24$
(2)
図のように、円周を10等分する点を取りました。点Oは円の中心、三角形ABCは正三角形です。
角アは$\Box$度、角イは$\Box$度、角ウは$\Box$度
(3)
図のように、長方形の紙を対角線を折り目としておりました。
斜線部分の面積は$\Box$㎠です。
(4)
図のように、棒を使って正三角形と正方形を作ります。
➀100個目の正方形を作り終えたとき、使った棒は$\Box$本です。
②棒が1000本ある時、正三角形は$\Box$個、正方形は$\Box$個まで作ることができます。
(5)
クラスの生徒に消しゴムを配ります。全員に10個ずつ配ると32個足りないので、先生と勝敗がつくまでじゃんけんをして、勝った人には11個、負けた人には7個配ることにしました。勝った人は負けた人よりも5人少なかったので、消しゴムは9個あまりました。
クラスの人数は$\Box$人、消しゴムは全部で$\Box$個です。
落とせば合格赤信号!2024女子御三家(桜蔭、女子学院、雙葉)計算問題5題」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学#雙葉中学
指導講師:
重吉
問題文全文(内容文):
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
この動画を見る
【2024年桜蔭中】
$16- ${$ 7 \displaystyle \frac{1}{3} \times 2.2-(5.7-4\displaystyle \frac{1}{6})\div 3\displaystyle \frac{2}{7} $}$=□$
$16-${$ \displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□}-(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\div \displaystyle \frac{□}{□}$ }
$=16-${$ \displaystyle \frac{□}{□} -(\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□})\times \displaystyle \frac{□}{□}$ }
$=16- (\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□} \times \displaystyle \frac{□}{□})$
$=16-(\displaystyle \frac{□}{□} -\displaystyle \frac{□}{□})$
$=16-\displaystyle \frac{□}{□} =\displaystyle \frac{□}{□}-\displaystyle \frac{□}{□}=\displaystyle \frac{□}{□}$
女子学院中2024年④「速さ」

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#女子学院中学
指導講師:
重吉
問題文全文(内容文):
【女子学院中】
はじめさんがA駅から家まで帰る方法は2通りあります。
-----------------
方法1:A駅から20km先にあるB駅まで電車で行き、B駅から家までは自転車で行く
方法2:A駅から18km先にあるC駅までバスで行き、C駅から家までは歩いて行く
-----------------
電車は時速75km、バスは時速40kmで進み、はじめさんが自転車で進む速さは、歩く速さよりも毎分116m速いです。
方法1と方法2のかかる時間はどちらも同じで、はじめさんが電車に乗る時間と自転車に乗る時間も同じです。
また、B駅から家までと、C駅から家までの道のりは合わせて3263mです。
C駅から家までの道のりは何mですか。
この動画を見る
【女子学院中】
はじめさんがA駅から家まで帰る方法は2通りあります。
-----------------
方法1:A駅から20km先にあるB駅まで電車で行き、B駅から家までは自転車で行く
方法2:A駅から18km先にあるC駅までバスで行き、C駅から家までは歩いて行く
-----------------
電車は時速75km、バスは時速40kmで進み、はじめさんが自転車で進む速さは、歩く速さよりも毎分116m速いです。
方法1と方法2のかかる時間はどちらも同じで、はじめさんが電車に乗る時間と自転車に乗る時間も同じです。
また、B駅から家までと、C駅から家までの道のりは合わせて3263mです。
C駅から家までの道のりは何mですか。
2023年女子学院中学校算数「時計算」

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#点の移動・時計算#女子学院中学
指導講師:
重吉
問題文全文(内容文):
時計Aは、月曜日18時から金曜日18時までは、24時間ごとに6分遅れていきます。
金曜日18時から土曜日10時40分までに、何分何秒遅れるかを求めよ
この動画を見る
時計Aは、月曜日18時から金曜日18時までは、24時間ごとに6分遅れていきます。
金曜日18時から土曜日10時40分までに、何分何秒遅れるかを求めよ
2023年女子学院中学校算数「規則性」

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#女子学院中学
指導講師:
重吉
問題文全文(内容文):
2023年女子学院中学校算数「規則性」
5つのランプがついていて、順にボタンを押していきます。
-----------------
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑪ …
A B C D E D C B A B C …
-----------------
(1)上図のようにCが10回目点灯するのは最初から数えて何回押されたときか求めよ
(2)150回目押したときに何が点灯しているか求めよ
(3)BとCだけが点灯している状態が1回だけある。200回目のとき、この状態は何回発生するか求めよ
この動画を見る
2023年女子学院中学校算数「規則性」
5つのランプがついていて、順にボタンを押していきます。
-----------------
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑪ …
A B C D E D C B A B C …
-----------------
(1)上図のようにCが10回目点灯するのは最初から数えて何回押されたときか求めよ
(2)150回目押したときに何が点灯しているか求めよ
(3)BとCだけが点灯している状態が1回だけある。200回目のとき、この状態は何回発生するか求めよ
女子学院中学校2023年「和差算、円、扇形の面積」
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#女子学院中学
指導講師:
重吉
問題文全文(内容文):
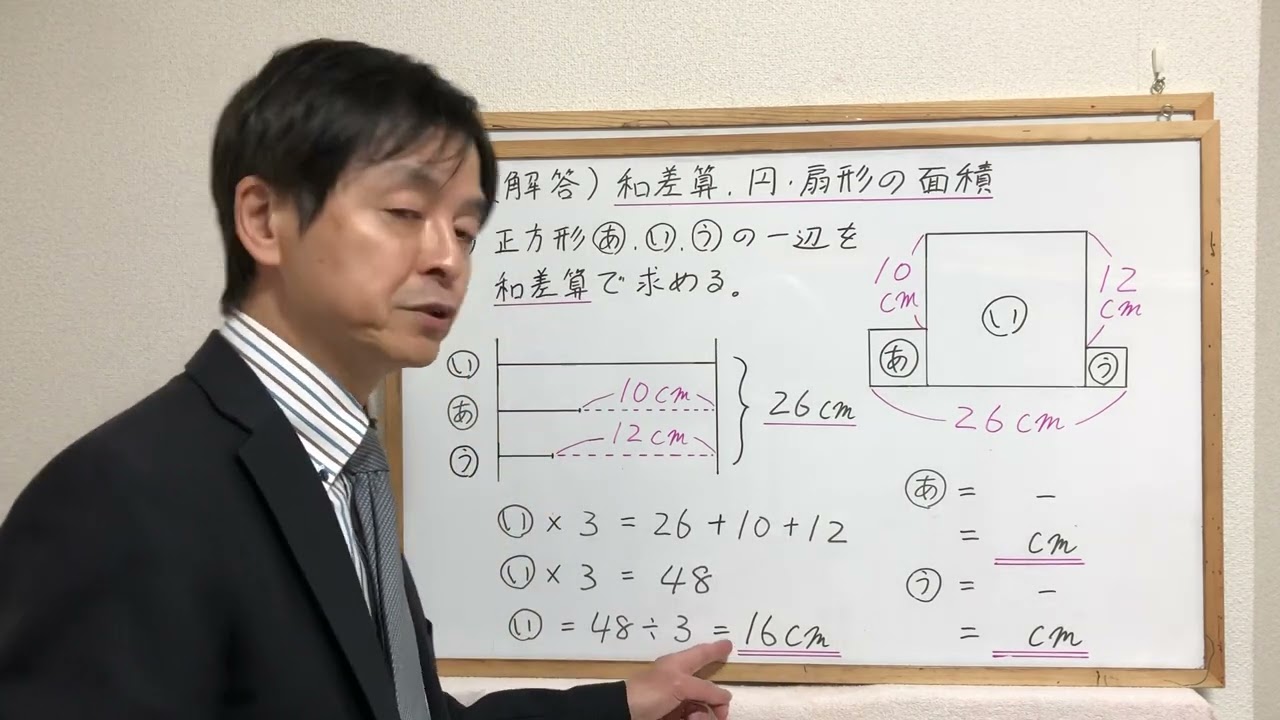
女子学院中学校2023年「和差算、円、扇形の面積」
※動画内の図を参照
(1)正方形あ、い、うの一辺を和差算で求めよ
(2)3個の扇の和を求めよ
この動画を見る
女子学院中学校2023年「和差算、円、扇形の面積」
※動画内の図を参照
(1)正方形あ、い、うの一辺を和差算で求めよ
(2)3個の扇の和を求めよ
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#女子学院中学#桜蔭中学
指導講師:
重吉
問題文全文(内容文):
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」
-----------------
(1)
$13 \displaystyle \frac{1}{3} - ${$(4\displaystyle \frac{13}{14} \times □-2.375) \div 1\displaystyle \frac{2}{11}-3\displaystyle \frac{5}{7}$}$=5\displaystyle \frac{11}{24}$
(2)
$5\displaystyle \frac{2}{3} \div 0.85 \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} +5.25)=□$
$\displaystyle \frac{□}{□} \div \displaystyle \frac{□}{□} \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} + \displaystyle \frac{□}{□})$
この動画を見る
2022年桜蔭中学校&女子学院中学校の入試問題「四則計算」
-----------------
(1)
$13 \displaystyle \frac{1}{3} - ${$(4\displaystyle \frac{13}{14} \times □-2.375) \div 1\displaystyle \frac{2}{11}-3\displaystyle \frac{5}{7}$}$=5\displaystyle \frac{11}{24}$
(2)
$5\displaystyle \frac{2}{3} \div 0.85 \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} +5.25)=□$
$\displaystyle \frac{□}{□} \div \displaystyle \frac{□}{□} \times \displaystyle \frac{37}{4} \times \displaystyle \frac{17}{25} - (\displaystyle \frac{13}{15} + \displaystyle \frac{□}{□})$
○○に気づけば楽勝です!適当に解くとミスる可能性大!こういう問題こそ論理的にきちんと解こう!【中学受験算数】【入試問題】【女子学院中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#女子学院中学#市川中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022市川中学校
ABCDEは正五角形FGHIは長方形㋐+㋑は何度?
2022女子学院中学校
2つの正方形を除いた部分の面積は?
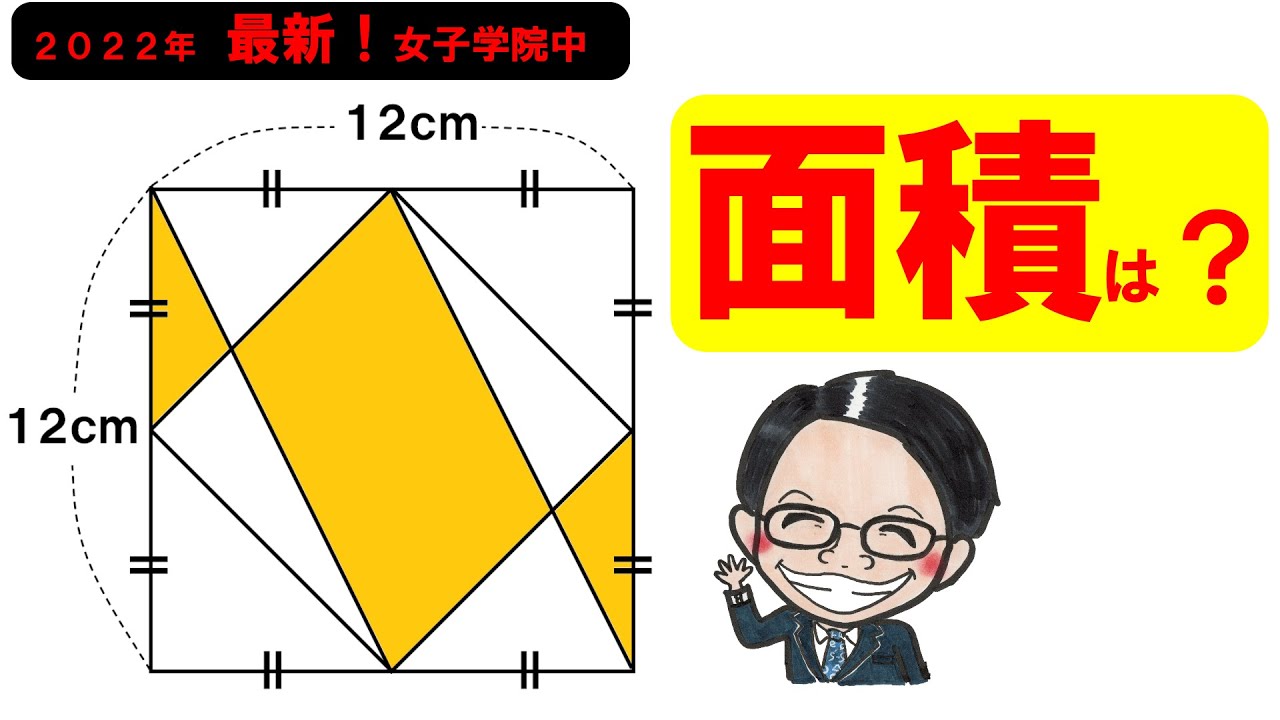
2022女子学院中学校
左図のABCDは正方形で同じ印をつけているところは同じ長さです。
斜線部の面積は?
*図は動画内参照
この動画を見る
2022市川中学校
ABCDEは正五角形FGHIは長方形㋐+㋑は何度?
2022女子学院中学校
2つの正方形を除いた部分の面積は?
2022女子学院中学校
左図のABCDは正方形で同じ印をつけているところは同じ長さです。
斜線部の面積は?
*図は動画内参照
【受験算数】平面図形:女子学院 半円と求積、弧の長さ

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#女子学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、直線アイの上に直径がある半円が4個ある。一番小さい半円は半径 10cmで、半径は大きくなるにつれて、前の半円の半径の1.5倍になっている(円周 率は3.14)。
(1)斜線部分の面積は何cm²ですか。答えは小数第4位を四捨五入する こと。
(2)太線の長さは何cmですか。
(3)一番大きい半円の中心は、一番小さい半 円の中心と比べて〈左・右〉に何cmだけ離れているでしょうか。
この動画を見る
図のように、直線アイの上に直径がある半円が4個ある。一番小さい半円は半径 10cmで、半径は大きくなるにつれて、前の半円の半径の1.5倍になっている(円周 率は3.14)。
(1)斜線部分の面積は何cm²ですか。答えは小数第4位を四捨五入する こと。
(2)太線の長さは何cmですか。
(3)一番大きい半円の中心は、一番小さい半 円の中心と比べて〈左・右〉に何cmだけ離れているでしょうか。
【受験算数】平面図形:女子学院2019年度大問1 四角形ABCDは正方形で点Oは円の中心、辺ABと直線EFは平行です。太線の図形は直線EFを対称の軸とした線対称な図形です。角ア~ウの大きさを求めよ。
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#女子学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
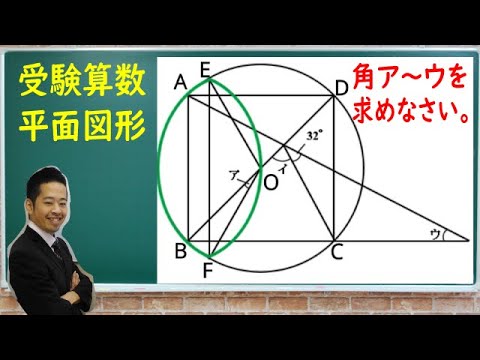
四角形ABCDは正方形で点Oは円の中心、辺ABと直線EFは平行です。太線の図形は直線EFを対称の軸とした線対称な図形です。角ア~ウの大きさを求めよ。
この動画を見る
四角形ABCDは正方形で点Oは円の中心、辺ABと直線EFは平行です。太線の図形は直線EFを対称の軸とした線対称な図形です。角ア~ウの大きさを求めよ。
