 開成中学
開成中学
 開成中学
開成中学
超ラッキー!開成中の計算問題 2025年開成中 #中学受験 #算数 #計算

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#文章題#単位・比と割合・比例・反比例#開成中学
指導講師:
重吉
問題文全文(内容文):
(0.02km+13m-40cm)×(2.3m+32cm-120mm)は何a(アール)ですか。
この動画を見る
(0.02km+13m-40cm)×(2.3m+32cm-120mm)は何a(アール)ですか。
超難関!開成中の楽勝計算問題!! 9で割ったあまりがすぐ出る裏ワザも公開!! #中学受験 #算数 #開成#御三家

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#開成中学
指導講師:
重吉
問題文全文(内容文):
次の計算の結果を9で割ったときのあまりを求めなさい。
1234567+2345671+3456712+4567123+5671234
この動画を見る
次の計算の結果を9で割ったときのあまりを求めなさい。
1234567+2345671+3456712+4567123+5671234
2025年開成中入試問題算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#開成中学
指導講師:
重吉
問題文全文(内容文):
大問1
(1) (0.02km + 13m - 40cm)(2.3m + 32cm - 120mm) は何aですか。
(2) ショウヘイ君はいくらかのお金を所持しています。まず、所持金の $\frac{1}{9}$より20円安い商品Aを買いました。次に、残金の$\frac{1}{7}$より40円安い商品Bを買いました。続けて、このときの残金の$\frac{1}{5}$より10円安い商品Cを買ったところ、最後に残ったお金ははじめの所持金の4割より480円多かったそうです。商品の値段はいくらでしたか。
この動画を見る
大問1
(1) (0.02km + 13m - 40cm)(2.3m + 32cm - 120mm) は何aですか。
(2) ショウヘイ君はいくらかのお金を所持しています。まず、所持金の $\frac{1}{9}$より20円安い商品Aを買いました。次に、残金の$\frac{1}{7}$より40円安い商品Bを買いました。続けて、このときの残金の$\frac{1}{5}$より10円安い商品Cを買ったところ、最後に残ったお金ははじめの所持金の4割より480円多かったそうです。商品の値段はいくらでしたか。
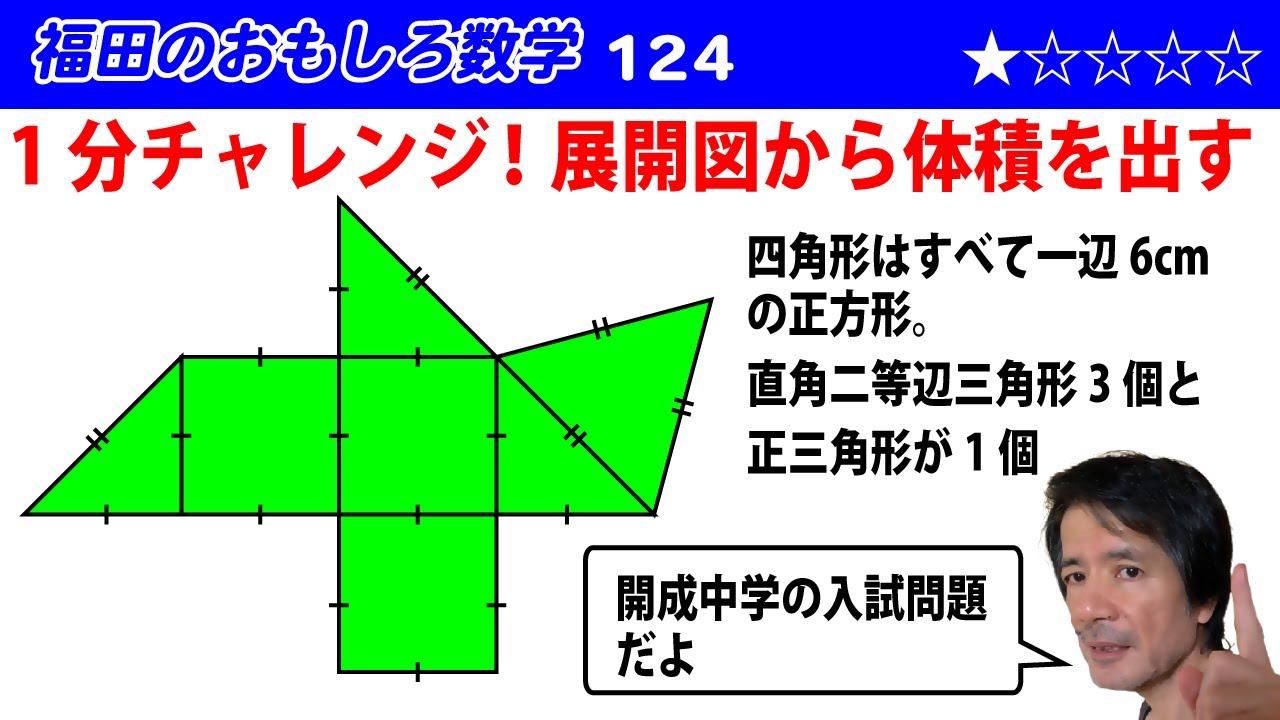
福田のおもしろ数学124〜展開図から立体の体積を求める
福田のおもしろ数学021〜開成中学入試問題だよ〜正六角形と正三角形の面積
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#開成中学
指導講師:
福田次郎
問題文全文(内容文):
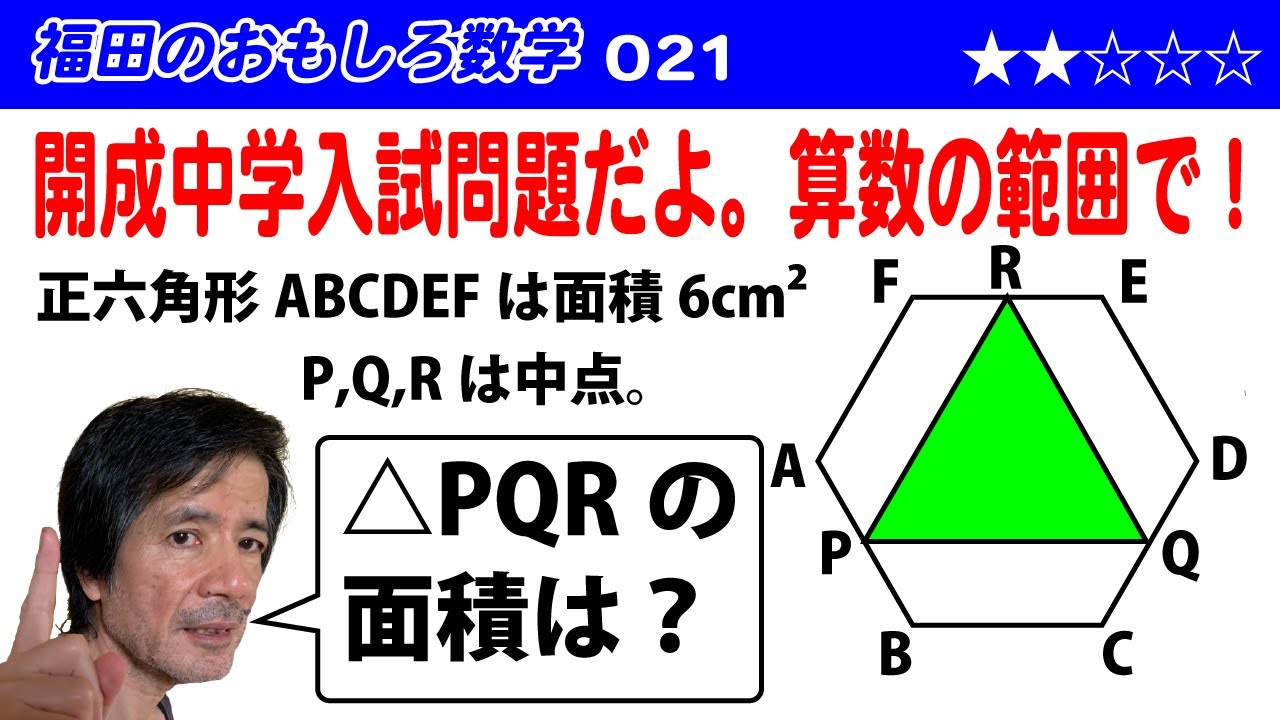
面積が$6cm^2$の正六角形 ABCDEF がある。図のように P, Q, R をそれぞれ辺 AB ,CD, EF の真ん中の点とする。三角形 PQR の面積を求めよ。
開成中過去問
この動画を見る
面積が$6cm^2$の正六角形 ABCDEF がある。図のように P, Q, R をそれぞれ辺 AB ,CD, EF の真ん中の点とする。三角形 PQR の面積を求めよ。
開成中過去問
開成中2023年1⃣「旅人算」解説
単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#開成中学
指導講師:
重吉
問題文全文(内容文):
開成中2023年1⃣「旅人算」解説
-----------------
ウサギとカメが競走をしました。
カメはスタート地点からゴール地点まで、毎分4mの速さで走り続けました。
ウサギはスタート地点をカメと同時に出発し、毎分60mの速さで走っていましたが、ゴール地点まで残り100mになったところで走るのをやめて、昼寝を始めました。
昼寝を始めた60分後に目を覚ましたウサギは、カメに追い抜かれていることに気がつきました。
あわてたウサギは、そこから毎分80mの速さでゴール地点まで走りましたが、ウサギがゴール地点に着いたのは、カメがゴール地点に着いた時刻の5秒後でした。
次の問いに答えなさい。
(1)ウサギが昼寝を始めてからカメがゴール地点に着くまでの時間は何分何秒ですか。
(2)ウサギが昼寝を始めたとき、ウサギはカメより何m先にいましたか。
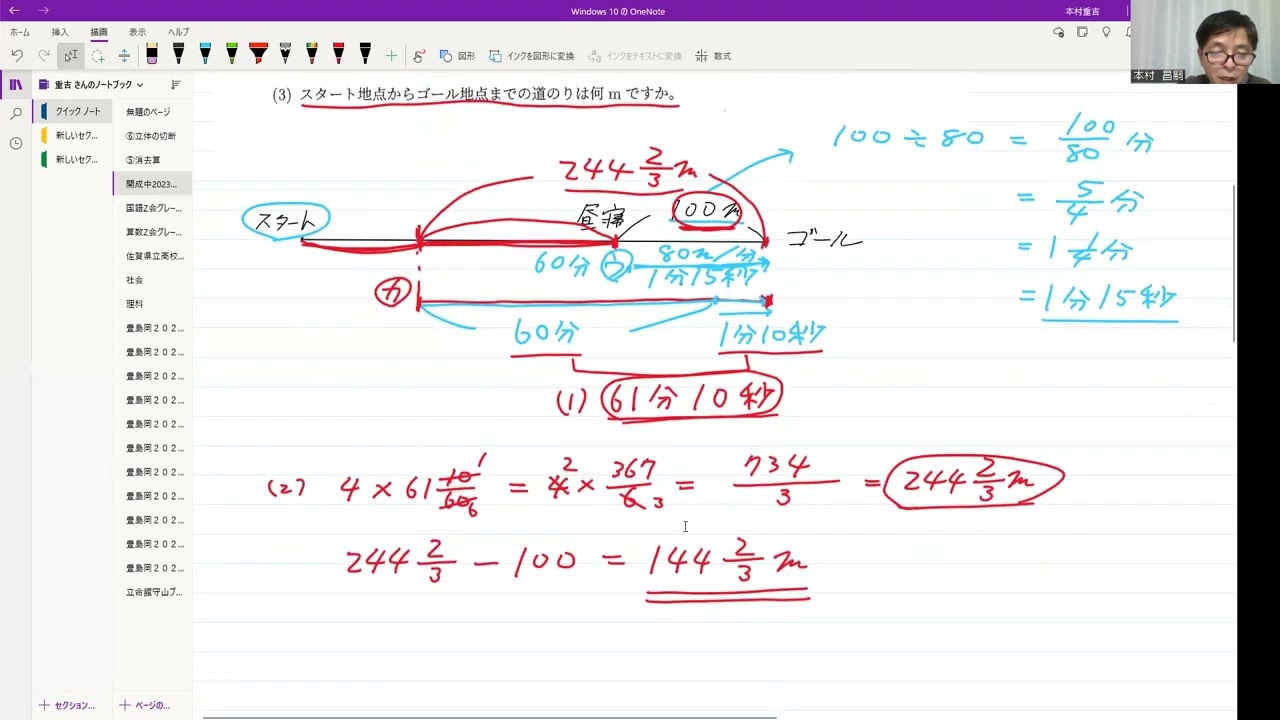
(3)スタート地点からゴール地点までの道のりは何mですか。
この動画を見る
開成中2023年1⃣「旅人算」解説
-----------------
ウサギとカメが競走をしました。
カメはスタート地点からゴール地点まで、毎分4mの速さで走り続けました。
ウサギはスタート地点をカメと同時に出発し、毎分60mの速さで走っていましたが、ゴール地点まで残り100mになったところで走るのをやめて、昼寝を始めました。
昼寝を始めた60分後に目を覚ましたウサギは、カメに追い抜かれていることに気がつきました。
あわてたウサギは、そこから毎分80mの速さでゴール地点まで走りましたが、ウサギがゴール地点に着いたのは、カメがゴール地点に着いた時刻の5秒後でした。
次の問いに答えなさい。
(1)ウサギが昼寝を始めてからカメがゴール地点に着くまでの時間は何分何秒ですか。
(2)ウサギが昼寝を始めたとき、ウサギはカメより何m先にいましたか。
(3)スタート地点からゴール地点までの道のりは何mですか。
小学生の知識だけで解くとヤバすぎる難問!○○を使った意外過ぎる解き方とは!?【中学受験算数】【入試問題】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#開成中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021開成中学校
面積が6㎠の正六角形ABCDEFがある。
三角形PQRは何㎠?
2021鎌倉学園中学校
下図は外側から正方形、円、正六角形、正三角形を組み合わせた図形です。正方形が8㎠のとき、太線で囲まれた面積の和は?(円周率は3.14)
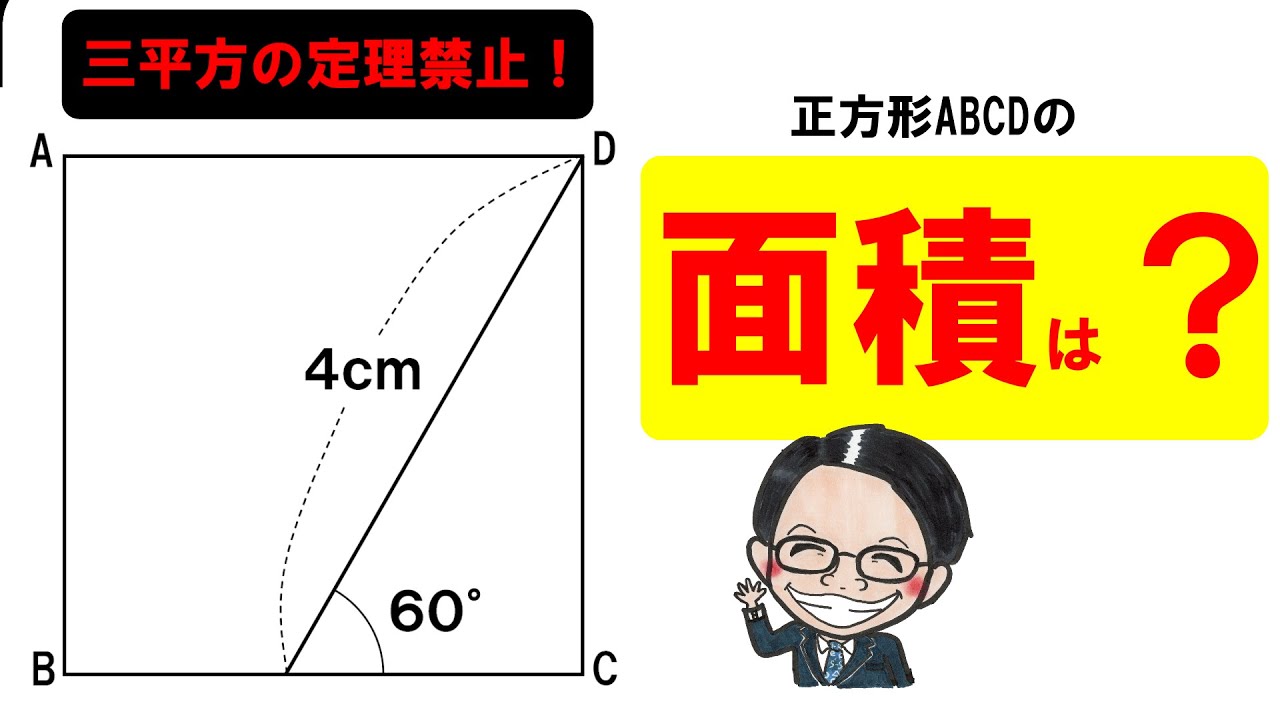
下図の正方形ABCDの面積は?(三平方を使わず求めよう)
*図は動画内参照
この動画を見る
2021開成中学校
面積が6㎠の正六角形ABCDEFがある。
三角形PQRは何㎠?
2021鎌倉学園中学校
下図は外側から正方形、円、正六角形、正三角形を組み合わせた図形です。正方形が8㎠のとき、太線で囲まれた面積の和は?(円周率は3.14)
下図の正方形ABCDの面積は?(三平方を使わず求めよう)
*図は動画内参照
開成中 秒殺だけど実は難問?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#開成中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1234567+2345671+3456712+$
$4567123+5671234$
を$9$で割った余りを求めよ.
2022開成中過去問
この動画を見る
$1234567+2345671+3456712+$
$4567123+5671234$
を$9$で割った余りを求めよ.
2022開成中過去問
【中学受験算数】100%解ける方法を伝授!単位分数の和で表す方法!開成中の難問にも対応可能!【毎日少しずつ中学受験算数73】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#開成中学
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣$\frac{11}{16} = \frac{1}{▢} + \frac{1}{△} + \frac{1}{○}$
2⃣$\frac{1}{4} = \frac{1}{▢} + \frac{1}{△} $
3⃣2010年開成中学校
$\frac{1}{12} = \frac{1}{△} + \frac{1}{▢} $(▢は△以上)
この動画を見る
1⃣$\frac{11}{16} = \frac{1}{▢} + \frac{1}{△} + \frac{1}{○}$
2⃣$\frac{1}{4} = \frac{1}{▢} + \frac{1}{△} $
3⃣2010年開成中学校
$\frac{1}{12} = \frac{1}{△} + \frac{1}{▢} $(▢は△以上)
開成中学 整数 等差数列の和

単元:
#算数(中学受験)#数列#数列とその和(等差・等比・階差・Σ)#過去問解説(学校別)#数学(高校生)#数B#開成中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
平方数を3つ以上の連続数の和で表す
(例)$6^2=1+2+3+…+8=11+12+13$
(1)
$7^2$
(2)
$10^2$
(3)
$30^2$は何通りあるか
出典:2018年開成中学校 過去問
この動画を見る
平方数を3つ以上の連続数の和で表す
(例)$6^2=1+2+3+…+8=11+12+13$
(1)
$7^2$
(2)
$10^2$
(3)
$30^2$は何通りあるか
出典:2018年開成中学校 過去問
