 慶應義塾湘南藤沢中等部
慶應義塾湘南藤沢中等部
 慶應義塾湘南藤沢中等部
慶應義塾湘南藤沢中等部
2025年慶應義塾湘南藤沢中 時計算 #中学受験 #算数 #慶應 #時計算

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
(問)
4時から5時までの間で、時計の長針と短針の作る角が90°になるのは4時イ分と4時ウ分である。ただし、イ<ウとする。
※図は動画内参照
この動画を見る
(問)
4時から5時までの間で、時計の長針と短針の作る角が90°になるのは4時イ分と4時ウ分である。ただし、イ<ウとする。
※図は動画内参照
慶應義塾湘南藤沢中等部2025年入試「場合の数」の解説です。

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#慶應義塾湘南藤沢中等部
指導講師:
問題文全文(内容文):
大小2つのサイコロをふって、大きいサイコロの目を十の位、小さくサイコロの目を一の位とする。この二けたの数が3の倍数になるのは▭通りである。
この動画を見る
大小2つのサイコロをふって、大きいサイコロの目を十の位、小さくサイコロの目を一の位とする。この二けたの数が3の倍数になるのは▭通りである。
2024年慶應義塾湘南藤沢中算数大問③、④中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#平面図形#図形の移動#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
3
図のようにマス目の中には「たての番号」×10+「よこの番号」を計算した数が書かれている。そして、「たての番号」と「よこの番号」の和をマス目の「番号和」と呼ぶことにする
例
➀「たての番号」が11、「よこの番号」が3のマス目には113が書かれ、このマスの「番号和」は14である。
②「たての番号」が3、「よこの番号」が11のマス目には41が書かれ、このマスの「番号和」は14である。
(1) 「番号和」が13になるマス目すべてに書かれている数のうち、最も大きいものと最も小さいものの和はいくつですか。
(2) 「番号和」が8になるマス目すべてに書かれている数の合計はいくつですか。
(3) 「番号和」がアになるマス目すべてに書かれている数の合計は1320である。アに入る数を求めなさい。
4
図1,2は1辺の長さが6 cmの正方形を一枚又は二枚使った図形である。これらの図形の周りを半径1 cmの円が転がりながら一周する。円周率は3.14として以下の問いに答えなさい。
(1) 図1において、円の中心が動く道のりを求めなさい。
(2) 図2において、円の中心が動く道のりを求めなさい。
(3) 図2において、円が通った後にできる部分の面積を求めなさい。
この動画を見る
※図は動画内参照
3
図のようにマス目の中には「たての番号」×10+「よこの番号」を計算した数が書かれている。そして、「たての番号」と「よこの番号」の和をマス目の「番号和」と呼ぶことにする
例
➀「たての番号」が11、「よこの番号」が3のマス目には113が書かれ、このマスの「番号和」は14である。
②「たての番号」が3、「よこの番号」が11のマス目には41が書かれ、このマスの「番号和」は14である。
(1) 「番号和」が13になるマス目すべてに書かれている数のうち、最も大きいものと最も小さいものの和はいくつですか。
(2) 「番号和」が8になるマス目すべてに書かれている数の合計はいくつですか。
(3) 「番号和」がアになるマス目すべてに書かれている数の合計は1320である。アに入る数を求めなさい。
4
図1,2は1辺の長さが6 cmの正方形を一枚又は二枚使った図形である。これらの図形の周りを半径1 cmの円が転がりながら一周する。円周率は3.14として以下の問いに答えなさい。
(1) 図1において、円の中心が動く道のりを求めなさい。
(2) 図2において、円の中心が動く道のりを求めなさい。
(3) 図2において、円が通った後にできる部分の面積を求めなさい。
2024年慶應義塾湘南藤沢中算数大問①② 中学受験指導20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
【1】ア、イ、ウにあてはまる数を求めなさい。
(1) $ 10 - \left( 20.24 + 17 \frac{\boxed{\text{ア}}}{25} \right) \div 9 = 5 \frac{4}{5} $
(2) $ \frac{1}{3 \times 6} + \frac{1}{6 \times 9} + \frac{1}{9 \times 12} + \frac{1}{12 \times 15} + \frac{1}{15 \times 18} = \boxed{\text{イ}} $
(3) $ 1 $ から $ 100 $ までの数から $ 4 $ の倍数と $ 6 $ の倍数を除いた数は全部で $ \boxed{\text{ウ}} $ 個ある。
【2】
(1) 1層 $ 672 \text{m} $ ある池の周りを、 $ K $ 君、$ O $ 君の2人が同じ地点から同時の出発し、それぞれ一定の速さで歩く。2人が反対方向に歩く場合は $ 6 $ 分後に初めて出会い、2人が同じ方向に歩く場合は $ 42 $ 分後に $ K $ 君は $ O $ 君を初めて追い越す。 $ K $ 君の歩く速さは毎分何 $ \text{m} $ ですか。
(2) 毎日決まった数だけを売れる $ 1 $ 個 $ 150 \text{円} $ の品物がある。今、売価を $ 20 \text{円} $ 値上げしたところ、1日の売り上げ個数は $ 1 $ 割減少したが、売り上げ高は $ 180 $ 円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3) 図のような長方形において、角 ㋐ の大きさを求めなさい。
※図は動画内参照。
この動画を見る
【1】ア、イ、ウにあてはまる数を求めなさい。
(1) $ 10 - \left( 20.24 + 17 \frac{\boxed{\text{ア}}}{25} \right) \div 9 = 5 \frac{4}{5} $
(2) $ \frac{1}{3 \times 6} + \frac{1}{6 \times 9} + \frac{1}{9 \times 12} + \frac{1}{12 \times 15} + \frac{1}{15 \times 18} = \boxed{\text{イ}} $
(3) $ 1 $ から $ 100 $ までの数から $ 4 $ の倍数と $ 6 $ の倍数を除いた数は全部で $ \boxed{\text{ウ}} $ 個ある。
【2】
(1) 1層 $ 672 \text{m} $ ある池の周りを、 $ K $ 君、$ O $ 君の2人が同じ地点から同時の出発し、それぞれ一定の速さで歩く。2人が反対方向に歩く場合は $ 6 $ 分後に初めて出会い、2人が同じ方向に歩く場合は $ 42 $ 分後に $ K $ 君は $ O $ 君を初めて追い越す。 $ K $ 君の歩く速さは毎分何 $ \text{m} $ ですか。
(2) 毎日決まった数だけを売れる $ 1 $ 個 $ 150 \text{円} $ の品物がある。今、売価を $ 20 \text{円} $ 値上げしたところ、1日の売り上げ個数は $ 1 $ 割減少したが、売り上げ高は $ 180 $ 円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3) 図のような長方形において、角 ㋐ の大きさを求めなさい。
※図は動画内参照。
2024年慶應義塾湘南藤沢中算数大問①② 中学受験指導20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#速さ#旅人算・通過算・流水算#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
この動画を見る
【1】$\boxed{ア}$, $\boxed{イ}$, $\boxed{ウ}$にあてはまる数を求めなさい。
(1)$10-(20.24+17\dfrac{\boxed{ ア }}{25})\div9=5\dfrac{4}{5}$
(2)$\dfrac{1}{3\times6}+\dfrac{1}{6\times9}+\dfrac{1}{9\times12}+\dfrac{1}{12\times15}+\dfrac{1}{15\times18}=\boxed{イ}$
(3)1から100までの数から4の倍数と6の倍数を除いた数は全部で$\boxed{ウ}$個である。
【2】
(1)1周672 mの池の周りを、K君、O君の二人が同じ地点から同時に出発し、それぞれ一定の速さで歩く。二人が反対方向に歩く場合は6分後に初めて出会い、2人が同じ方向に歩く場合は42分後にK君がO君を初めて追い越す。K君の歩く速さは毎分何mですか。
(2)毎日決まった数だけ売れる1個150円の品物がある。今、売上を20円値上げしたところ、1日の売り上げ個数は1割減少したが、売上高は180円増加した。この品物の、値上げ前の1日の売り上げ個数は何個ですか。
(3)図のような長方形において、角㋐の大きさを求めなさい。
※図は動画内参照
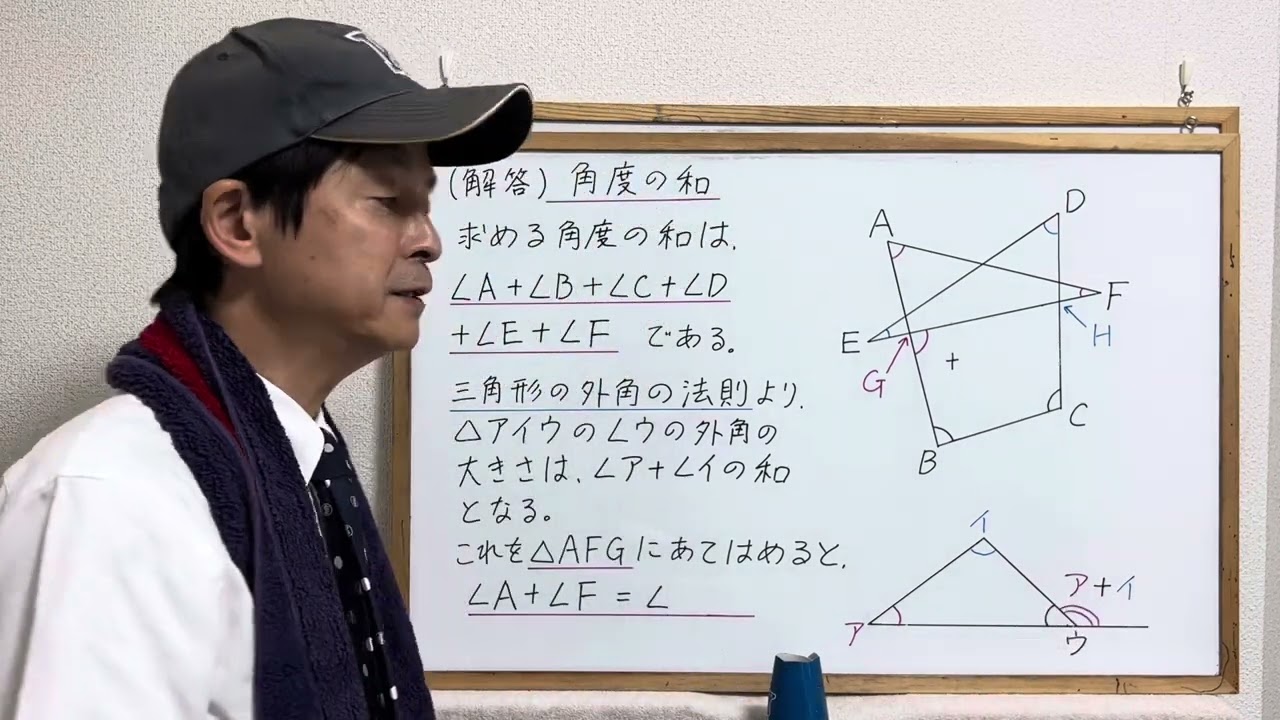
2023年慶応義塾湘南藤沢中等部算数「角度の和」
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#慶應義塾湘南藤沢中等部
指導講師:
重吉
問題文全文(内容文):
2023年慶応義塾湘南藤沢中等部算数「角度の和」
6つの印がついた角度の和を求めよ
※動画内の図を参照
この動画を見る
2023年慶応義塾湘南藤沢中等部算数「角度の和」
6つの印がついた角度の和を求めよ
※動画内の図を参照
