 豊島岡女子学園中学
豊島岡女子学園中学
 豊島岡女子学園中学
豊島岡女子学園中学
目指せ合格!豊島岡女子 最小公倍数2025 #中学受験 #算数 #計算 #最小公倍数

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
405と( )の最大公約数は45、最小公倍数は2025です。( )にあてはまる値を求めよ。
この動画を見る
405と( )の最大公約数は45、最小公倍数は2025です。( )にあてはまる値を求めよ。
2025年豊島岡女子学園中入試算数大問① 中学受験指導歴20年プロ塾講師のじっくり解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
この動画を見る
(1)
\[
\left( 77 \div 17 - 3\frac{1}{34} \right) \times \left( \frac{4}{9} - \frac{3}{7} \right)
\]
を計算しなさい。
(2) 1,2,3,5,6,7,8,10,11, 12, 13, 15, ......
のように、4と9を使うことなく1から順に整数を並べたとき,85は小さい方から数えて何番目ですか。
(3) お菓子をあるグループに1人4個ずつ配ろうとすると23個余り、1人6個ずつ配ろうとすると、最後から3人目の人に配っている途中でなくなり、最後の2人は 1個ももらえないそうです。このグループの人数として考えられる最も多い人数は何人ですか。
(4)405と□の最大公約数は45, 最小公倍数は2025です。
□にあてはまる数はいくつですか。
2024年豊島岡女子学園中算数大問②(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#仕事算とニュートン算#平均算・過不足算・差集め算・消去算#平面図形#角度と面積#相似と相似を利用した問題#場合の数#場合の数#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
(1)
ある水槽には管A、管B、管Cの三つの水を入れる管がついています。空の状態から、管Aのみを20分間用いると水槽がいっぱいになり、管Aを5分間、管Bと管Cを18分間用いると水槽がいっぱいになります。また、管Aを8分間、管Bを17分間、管Cを12分間用いると水槽がいっぱいになります。管Bからは毎分1Lの水が出るとき、水槽の容積は何Lですか。
(2)
バスケットボールの試合では、シュートの種類によって1点、2点、3点の得点を取ることができます。豊子さんはある試合で10点を取りました。シュートの種類の組み合わせは全部で何通りありますか。ただし、得点の順番は考えないものとします。
(3)
正三角形ABCDEFGHIJがあります。図のように点Bを中心とし、点Dを通る円の弧DJと点Jを中心とし、点Bを通る円の弧BHの交わる点をKとします。このとき、角CDKの大きさは何度ですか。
※図は動画内参照
(4)
図のようにAB = AC = 3 cm, BC = 2cm の二等辺三角形ABCとDE = DF = 3 cm, EF = 2 cm の二等辺三角形DEFがあります。点Eは辺BCの真ん中の点であり、点Gは辺EFの真ん中のt点で、辺AC上にあります。辺ABと辺DFの交わる点をHとするとき、DHの長さは何cmですか。
※図は動画内参照
この動画を見る
(1)
ある水槽には管A、管B、管Cの三つの水を入れる管がついています。空の状態から、管Aのみを20分間用いると水槽がいっぱいになり、管Aを5分間、管Bと管Cを18分間用いると水槽がいっぱいになります。また、管Aを8分間、管Bを17分間、管Cを12分間用いると水槽がいっぱいになります。管Bからは毎分1Lの水が出るとき、水槽の容積は何Lですか。
(2)
バスケットボールの試合では、シュートの種類によって1点、2点、3点の得点を取ることができます。豊子さんはある試合で10点を取りました。シュートの種類の組み合わせは全部で何通りありますか。ただし、得点の順番は考えないものとします。
(3)
正三角形ABCDEFGHIJがあります。図のように点Bを中心とし、点Dを通る円の弧DJと点Jを中心とし、点Bを通る円の弧BHの交わる点をKとします。このとき、角CDKの大きさは何度ですか。
※図は動画内参照
(4)
図のようにAB = AC = 3 cm, BC = 2cm の二等辺三角形ABCとDE = DF = 3 cm, EF = 2 cm の二等辺三角形DEFがあります。点Eは辺BCの真ん中の点であり、点Gは辺EFの真ん中のt点で、辺AC上にあります。辺ABと辺DFの交わる点をHとするとき、DHの長さは何cmですか。
※図は動画内参照
2024年豊島岡女子学園中算数大問①(1)~(4)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算#平均算・過不足算・差集め算・消去算#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
次の各問いに答えなさい。
(1)$2024\div3\times\{ (0.32+\dfrac{2}{5})\div\dfrac{4}{15}\div9.9 \}$を計算しなさい。
(2)中学1年生に用意した鉛筆を配りました。1人に3本ずつ配ると88本あまり、1人に5本ずつ配ると4本不足しました。用意したえんぴつは全部で何本でしたか。
(3)Aさんの所持金の半分の金額と、Bさんの所持金の40 %の金額は同じ金額です。また、Aさんの所持金に1800円を加えた金額とBさんの所持金の2倍の金額は同じ金額です。Aさんの所持金はいくらですか。
(4)下の図の〇の中に1から10までの異なる整数を書き入れ、(あ)から(け)までの9つの三角形の頂点の3つの数を足します。このようにしてできた9つの数の和が最も小さくなるような数を書き入れるとき、その和を答えなさい。
※図は動画内参照
この動画を見る
次の各問いに答えなさい。
(1)$2024\div3\times\{ (0.32+\dfrac{2}{5})\div\dfrac{4}{15}\div9.9 \}$を計算しなさい。
(2)中学1年生に用意した鉛筆を配りました。1人に3本ずつ配ると88本あまり、1人に5本ずつ配ると4本不足しました。用意したえんぴつは全部で何本でしたか。
(3)Aさんの所持金の半分の金額と、Bさんの所持金の40 %の金額は同じ金額です。また、Aさんの所持金に1800円を加えた金額とBさんの所持金の2倍の金額は同じ金額です。Aさんの所持金はいくらですか。
(4)下の図の〇の中に1から10までの異なる整数を書き入れ、(あ)から(け)までの9つの三角形の頂点の3つの数を足します。このようにしてできた9つの数の和が最も小さくなるような数を書き入れるとき、その和を答えなさい。
※図は動画内参照
豊島岡女子学園中2024年算数入試問題「面積の和(3)」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような直角三角形PQRと正方形STUVがあります。
辺QRの長さと正方形の1辺の長さが等しく、辺PRの長さと正方形の1辺の長さの和が4cmであるとき、2つの図形の面積の和は何cmですか。
この動画を見る
動画内の図のような直角三角形PQRと正方形STUVがあります。
辺QRの長さと正方形の1辺の長さが等しく、辺PRの長さと正方形の1辺の長さの和が4cmであるとき、2つの図形の面積の和は何cmですか。
2024年豊島岡女子学園中算数「面積の和(2)」個別指導塾講師歴20年のプロ解説
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
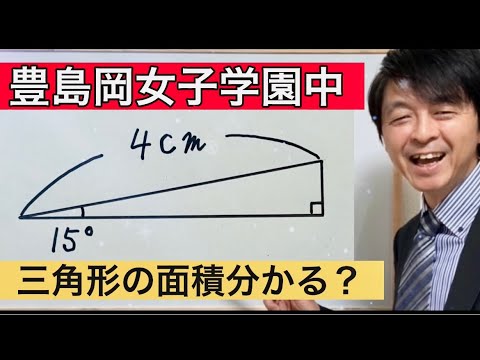
動画内の図のような三角形GHI,JKL,MNOがあります。
辺GIの長さと辺JKの長さ、辺の長さと辺NOの長さがそれぞれ等しく、辺GHの長さと辺MNの長さの和が4cmであるとき、3つの三角形の面積の和は何cm²ですか。
この動画を見る
動画内の図のような三角形GHI,JKL,MNOがあります。
辺GIの長さと辺JKの長さ、辺の長さと辺NOの長さがそれぞれ等しく、辺GHの長さと辺MNの長さの和が4cmであるとき、3つの三角形の面積の和は何cm²ですか。
福田の中学入試の算数004〜豊島岡女子学園中学校2011年〜円の一部分の面積を求める
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
福田次郎
問題文全文(内容文):
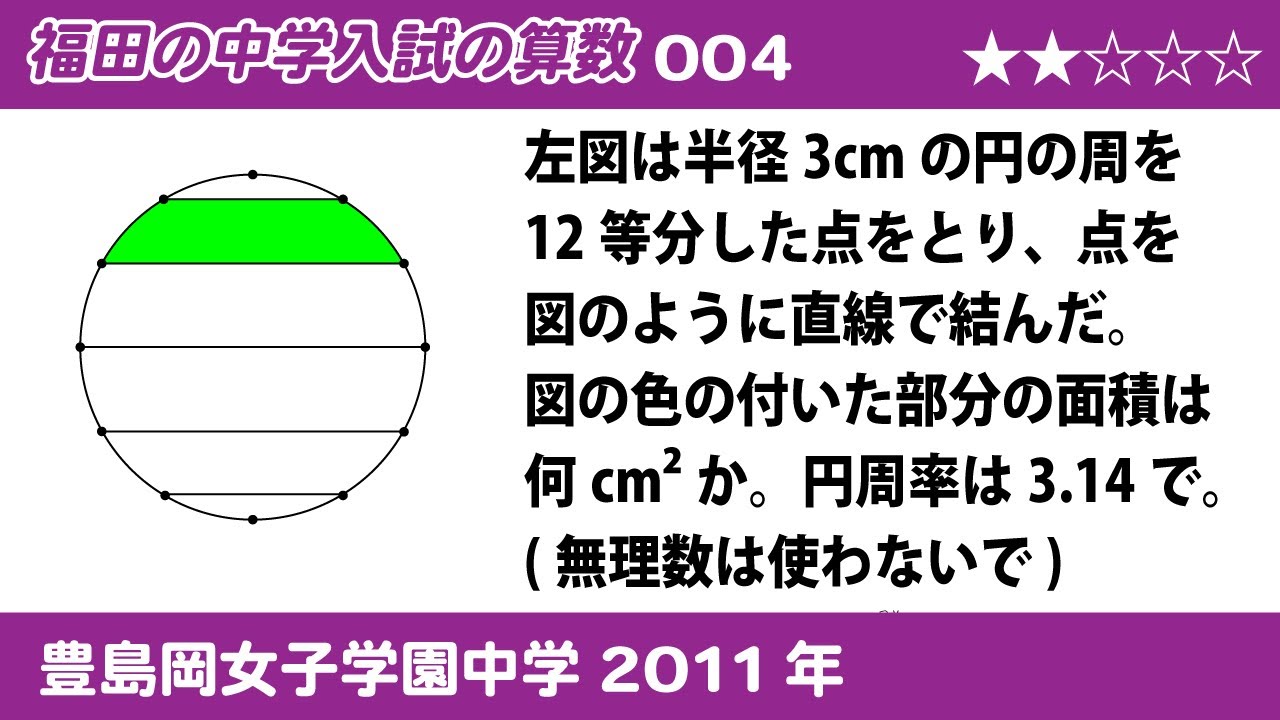
左図(※動画参照)は半径3 cmの円の周を12等分した点をとり、点を図のように直線で結んだ。
図の色の付いた部分の面積は何 $\textrm{cm}^2$か。円周率は3.14とする。
この動画を見る
左図(※動画参照)は半径3 cmの円の周を12等分した点をとり、点を図のように直線で結んだ。
図の色の付いた部分の面積は何 $\textrm{cm}^2$か。円周率は3.14とする。
豊島岡女子学園中2024年算数入試問題「面積の和(1)」個別指導塾講師歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
動画内の図のような三角形ABC,DEFがあります。
辺ACの長さと辺DEの長さが等しく、辺ABと辺DFの長さの和が4cmであるとき、2つの三角形の面積の和は何cm²ですか。
この動画を見る
動画内の図のような三角形ABC,DEFがあります。
辺ACの長さと辺DEの長さが等しく、辺ABと辺DFの長さの和が4cmであるとき、2つの三角形の面積の和は何cm²ですか。
2023年豊島岡女子学園中学校算数「売買損益」

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#豊島岡女子学園中学
指導講師:
重吉
問題文全文(内容文):
【売買損益】
(1)仕入れ値を①とすると、5割増しの定価は、
定価:①$\times (1+$____)=〇
売り値は、定価の2割引きなので、
売り値:$○ \times(1-$____)=〇$\times$ ____=〇
「売り値-仕入れ値=利益」より
〇-〇=____円
〇=____円
仕入れ値①=____円$\div$____=____円
(2)定価は、仕入れ値120円の5割増しなので、
定価:____$\times (1+$____) = ____ $\times$ ____ = ____円
よって、定価で1個売れた場合の利益は、
____円 - ____円 = ____円なので、定価で____個売れた分の利益は、
____円$\times$____個=____円
全体の利益は、43,800円なので、2割引きの値段で売った分の利益は、
____ - ____ = ____円
定価____円の2割引きの売り値は、____円$\times(1-$____)= ____円$\times$____ = ____円
値引き価格で1個売れた場合の利益は、____円 - ____円 = ____円
よって、2割引きで売れた個数は、____ ÷ ____ = ____個
仕入れ数=定価で売れた分+値引き分=____個 + ____個 = ____個
この動画を見る
【売買損益】
(1)仕入れ値を①とすると、5割増しの定価は、
定価:①$\times (1+$____)=〇
売り値は、定価の2割引きなので、
売り値:$○ \times(1-$____)=〇$\times$ ____=〇
「売り値-仕入れ値=利益」より
〇-〇=____円
〇=____円
仕入れ値①=____円$\div$____=____円
(2)定価は、仕入れ値120円の5割増しなので、
定価:____$\times (1+$____) = ____ $\times$ ____ = ____円
よって、定価で1個売れた場合の利益は、
____円 - ____円 = ____円なので、定価で____個売れた分の利益は、
____円$\times$____個=____円
全体の利益は、43,800円なので、2割引きの値段で売った分の利益は、
____ - ____ = ____円
定価____円の2割引きの売り値は、____円$\times(1-$____)= ____円$\times$____ = ____円
値引き価格で1個売れた場合の利益は、____円 - ____円 = ____円
よって、2割引きで売れた個数は、____ ÷ ____ = ____個
仕入れ数=定価で売れた分+値引き分=____個 + ____個 = ____個
【受験算数】豊島岡過去問~正方形をはみ出る円の面積の求め方

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#豊島岡女子学園中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2010年豊島岡大問2(4)の図形問題です。
右の図のように、1辺の長さが3㎝の正方形の辺をそれぞれ3等分した点をすべて通る円があります。この円の面積は何㎠ですか。
この動画を見る
2010年豊島岡大問2(4)の図形問題です。
右の図のように、1辺の長さが3㎝の正方形の辺をそれぞれ3等分した点をすべて通る円があります。この円の面積は何㎠ですか。
え!?これだけの情報で解けるの?実は○○を使えば解けるんです!さあ、あなたは解けるかな?【中学受験算数】【入試問題】【西大和学園中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学#西大和学園中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022豊島岡女子学園中学校
左図の正方形ABCDで斜線部分の面積は?
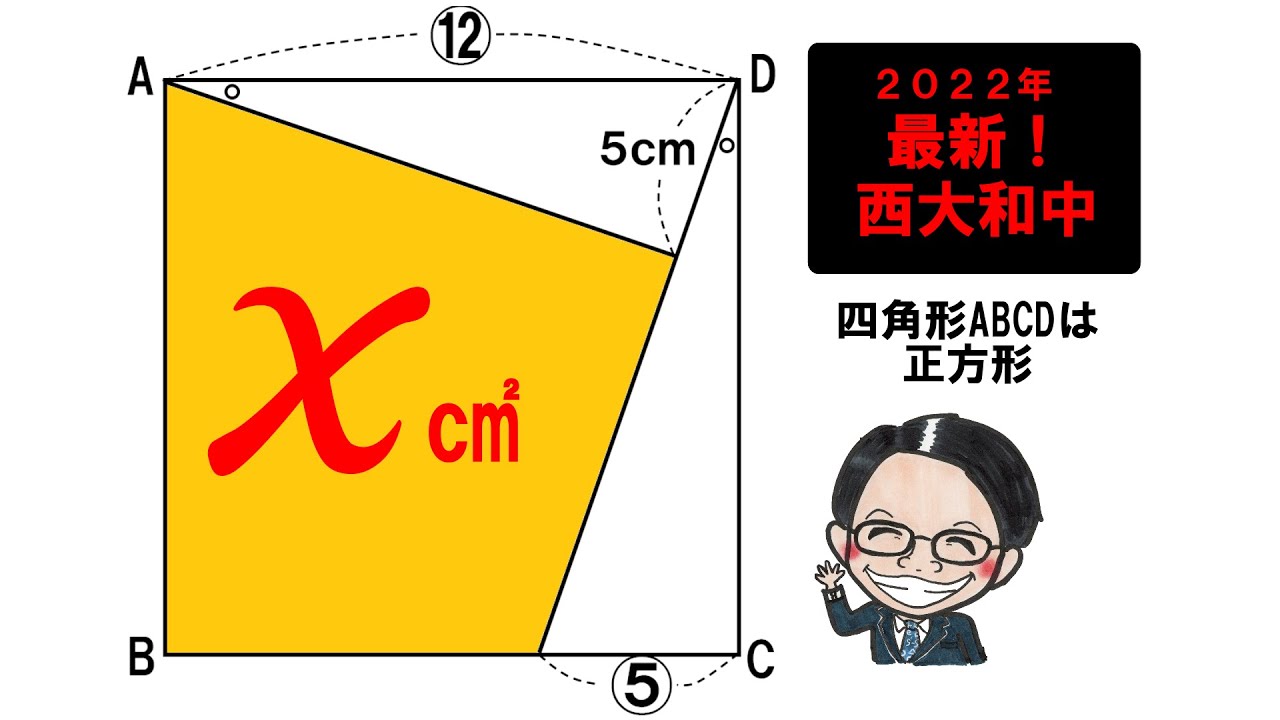
2022西大和学園中学校
左図の四角形ABCDは正方形で、(ADの長さ):(CEの長さ)=12:5となるように辺BC上に点Eをとる。図の○のついた角の大きさが同じになるようにDE上に点FをとったとこりDFの長さが5㎝となった。
四角形ABEFの面積は?
*図は動画内参照
この動画を見る
2022豊島岡女子学園中学校
左図の正方形ABCDで斜線部分の面積は?
2022西大和学園中学校
左図の四角形ABCDは正方形で、(ADの長さ):(CEの長さ)=12:5となるように辺BC上に点Eをとる。図の○のついた角の大きさが同じになるようにDE上に点FをとったとこりDFの長さが5㎝となった。
四角形ABEFの面積は?
*図は動画内参照
【受験算数】平面図形:豊島岡女子(2019年)ロープに繋がれた牛が動くことのできる部分の面積は?
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#図形の移動#豊島岡女子学園中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
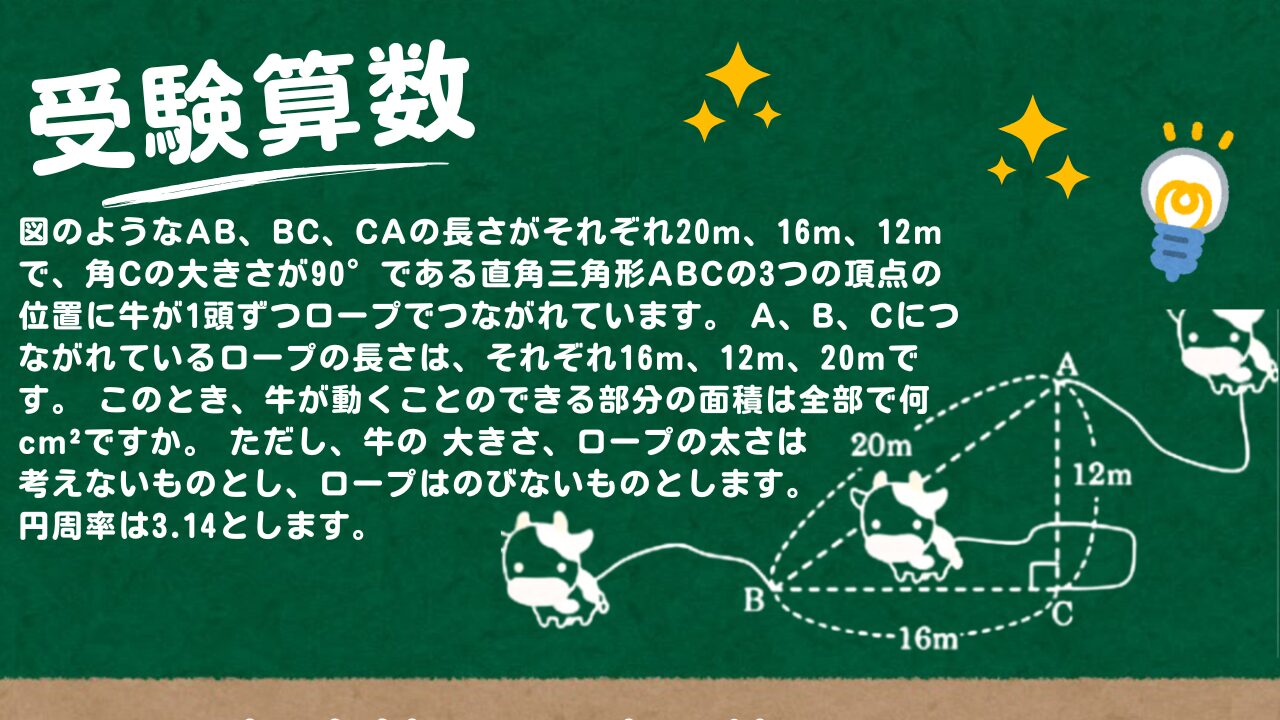
図のようなAB、BC、CAの長さがそれぞれ20m、16m、12mで、角Cの大きさが90°である直角三角形ABCの3つの頂点の位置に牛が1頭ずつロープでつながれています。
A、B、Cにつながれているロープの長さは、それぞれ16m、12m、20mです。
このとき、牛が動くこ とのできる部分の面積は全部で何cm²ですか。
ただし、牛の 大きさ、ロープの太さは考えないものとし、ロープはのびないものとします。
円周率は3.14とします。
この動画を見る
図のようなAB、BC、CAの長さがそれぞれ20m、16m、12mで、角Cの大きさが90°である直角三角形ABCの3つの頂点の位置に牛が1頭ずつロープでつながれています。
A、B、Cにつながれているロープの長さは、それぞれ16m、12m、20mです。
このとき、牛が動くこ とのできる部分の面積は全部で何cm²ですか。
ただし、牛の 大きさ、ロープの太さは考えないものとし、ロープはのびないものとします。
円周率は3.14とします。
【受験算数】平面図形:豊島岡女子(2021年) 三角形の面積比
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#豊島岡女子学園中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
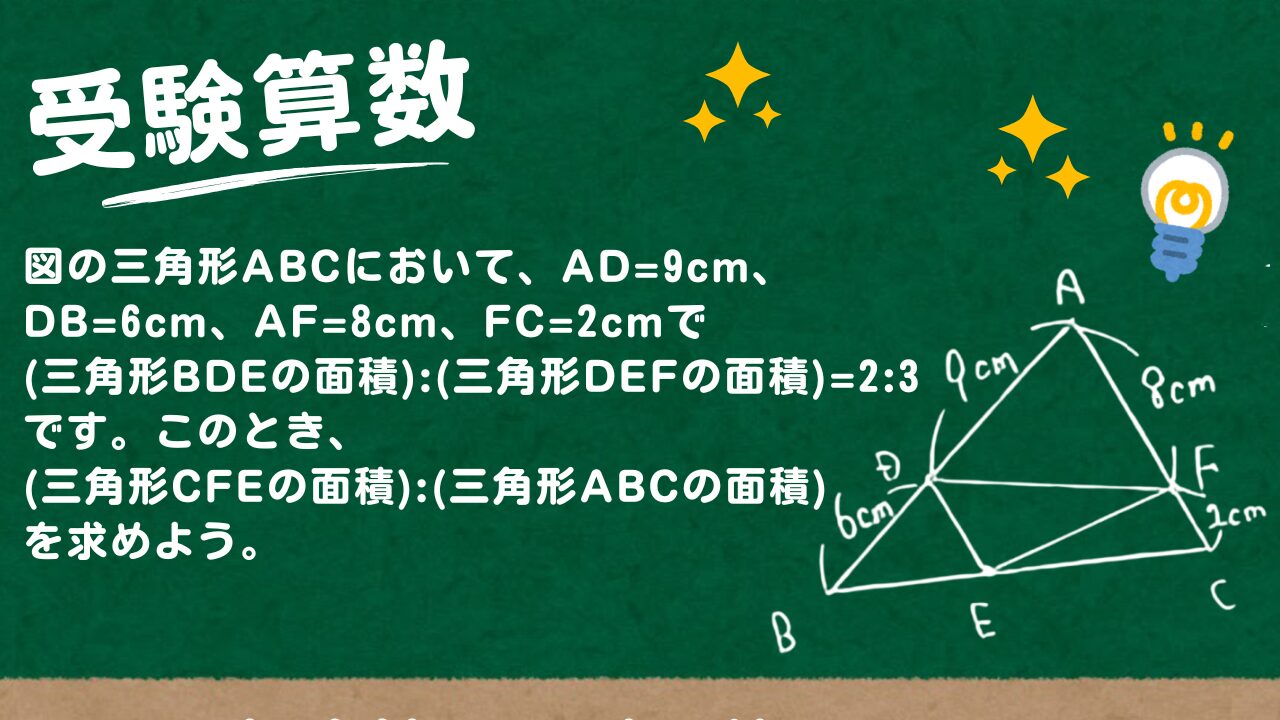
図の三角形ABCにおいて、AD=9cm、DB=6cm、AF=8cm、FC=2cmで (三角形BDEの面積):(三角形DEFの面積)=2:3です。このとき、(三角形CFEの面 積):(三角形ABCの面積)を求めよう。
この動画を見る
図の三角形ABCにおいて、AD=9cm、DB=6cm、AF=8cm、FC=2cmで (三角形BDEの面積):(三角形DEFの面積)=2:3です。このとき、(三角形CFEの面 積):(三角形ABCの面積)を求めよう。
