 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
【小6算数手元解説】受験算数 速さ⑩【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは2時間42分、 帰りは2時間18分かかりました。平地は時速5km、上りは時速4km、下りは時速6kmで歩きました。次の問いに答えなさい。
(1) B、C間の距離は何 kmですか。
(2) A、B間の距離は何 kmですか。
この動画を見る
A地点からB地点までは平地で、C地点は山頂です。いまAから出発してA、C間を往復するのに、行きは2時間42分、 帰りは2時間18分かかりました。平地は時速5km、上りは時速4km、下りは時速6kmで歩きました。次の問いに答えなさい。
(1) B、C間の距離は何 kmですか。
(2) A、B間の距離は何 kmですか。
小学生でも簡単!?思わず「なるほど~」とつぶやく良問!【中学受験算数】
【小6算数手元解説】受験算数 時計算④【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
2時と3時の間で、時計の長針と短針が文字ばんの数字4を中心にして等しい 角度になっている時刻は何時何分ですか。
この動画を見る
2時と3時の間で、時計の長針と短針が文字ばんの数字4を中心にして等しい 角度になっている時刻は何時何分ですか。
【算数練習】152(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
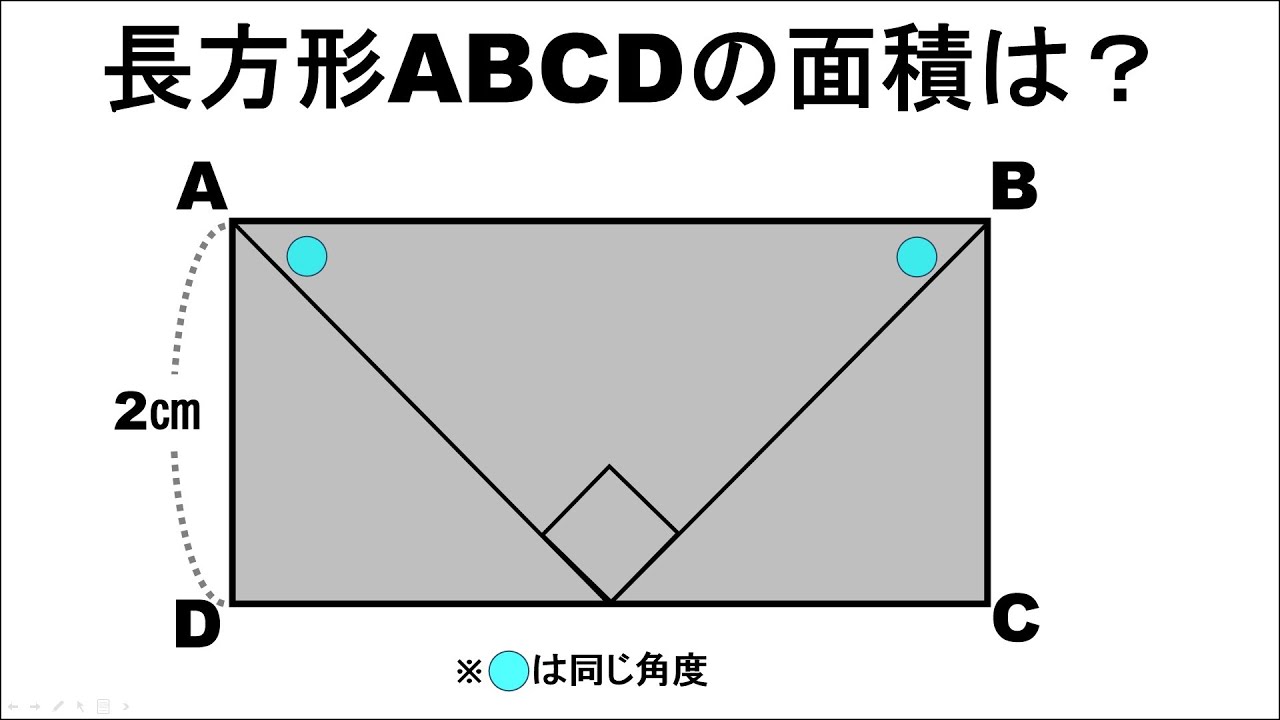
長方形ABCDがあり、A,Bから辺CDの中点に向かって線が引かれている。
長方形ABCDの面積は?
※図は動画内参照
この動画を見る
長方形ABCDがあり、A,Bから辺CDの中点に向かって線が引かれている。
長方形ABCDの面積は?
※図は動画内参照
この問題分かる?

【算数練習】149(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
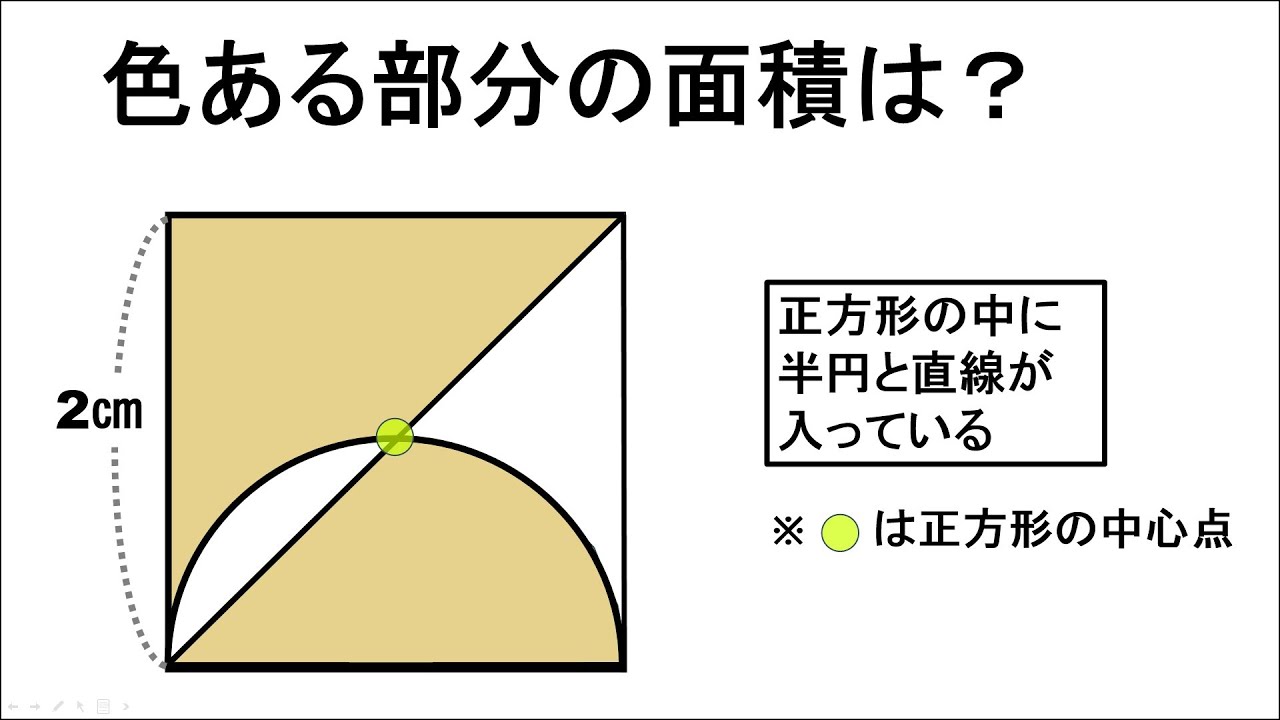
正方形の中に半円と直線が入っている
色のある部分の面積は?
※図は動画内参照
この動画を見る
正方形の中に半円と直線が入っている
色のある部分の面積は?
※図は動画内参照
【小6算数手元解説】受験算数 時計算③【問題文は概要欄】

単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
2時と3時の間で、時計の長針と短針が文字ばんの数字2を中心にして等しい 角をつくる時刻は何時何分ですか。
この動画を見る
2時と3時の間で、時計の長針と短針が文字ばんの数字2を中心にして等しい 角をつくる時刻は何時何分ですか。
簡単そう?いや、意外と難問です!灘中学校の面白い問題!【中学受験算数】
【小5算数解説】受験算数 流水算D2:川に帽子を落とした 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
この動画を見る
毎時3kmの速さで流れている川の上流にP市があり、P市の120km下流にQ市があります。Aさんは静水時の速さが毎時12kmの船に乗ってP市からQ市に向かって出発しましたが、出発してから6時間後に川に帽子を落としてしまいました。Aさんは帽子を落としたことに途中で気づき、Q市につくとすぐに船で帽子を拾いに戻ったところ、川に流されてきた帽子を拾うことができました。
(1)AさんがQ市についたとき、帽子はQ市から何kmのところにありますか。
(2)Aさんが帽子を拾うことができたのはQ市から何kmのところですか。
【小5算数解説】受験算数 流水算D1:休みながら進む 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時4kmの速さで流れている川の上流にP市があり、P市の100km下流にQ市があります。流れがないところで毎時12kmの速さで船をこぐ水夫がQ市からP市に向かって出発しましたが、この水夫は3時間進むごとに1時間こぐのをやめます。このとき、次の問に答えなさい。
(1)出発してから4時間後に船はQ市から何kmのところにいますか。
(2) P市につくのは、Q市を出発してから何時間何分後ですか。
この動画を見る
毎時4kmの速さで流れている川の上流にP市があり、P市の100km下流にQ市があります。流れがないところで毎時12kmの速さで船をこぐ水夫がQ市からP市に向かって出発しましたが、この水夫は3時間進むごとに1時間こぐのをやめます。このとき、次の問に答えなさい。
(1)出発してから4時間後に船はQ市から何kmのところにいますか。
(2) P市につくのは、Q市を出発してから何時間何分後ですか。
【中学受験問題に挑戦】138(”大人”は頭の体操) 三角形の考察
【小5算数解説】受験算数 流水算C3:帰りに出会う 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時4kmの速さで流れている川の上流にP市があり、P市の90km下流にQ市があります。静水時の速さが毎時11kmのA船と、静水時 の速さが毎時7kmのB船が、同時にP市を出発してQ市との間を途中で休まずに1往復します。このとき、次の問に答えなさい。
(1)A船がQ市についたとき、B船はQ市まであと何kmのところにいますか。
(2)B船がQ市から戻ってくるA船と出会うのは、P市を出発してから何時間何分後ですか。
この動画を見る
毎時4kmの速さで流れている川の上流にP市があり、P市の90km下流にQ市があります。静水時の速さが毎時11kmのA船と、静水時 の速さが毎時7kmのB船が、同時にP市を出発してQ市との間を途中で休まずに1往復します。このとき、次の問に答えなさい。
(1)A船がQ市についたとき、B船はQ市まであと何kmのところにいますか。
(2)B船がQ市から戻ってくるA船と出会うのは、P市を出発してから何時間何分後ですか。
【小5算数解説】受験算数 流水算C2:真ん中からずれ出会う 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
120km離れた川の川上のP町からA船が、川下のQ町からB船が向かい合って同時に出発しました。A船の静水時の速さは時速9km、B船の静水時の速さは時速11kmです。2つの船が出会った地点は、P町とQ町のちょうど真ん中よりQ町に6km近いところでした。
(1)2つの船は出発してから何時間後に出会いますか。
(2)この川の流れの速さは時速何kmですか。
この動画を見る
120km離れた川の川上のP町からA船が、川下のQ町からB船が向かい合って同時に出発しました。A船の静水時の速さは時速9km、B船の静水時の速さは時速11kmです。2つの船が出会った地点は、P町とQ町のちょうど真ん中よりQ町に6km近いところでした。
(1)2つの船は出発してから何時間後に出会いますか。
(2)この川の流れの速さは時速何kmですか。
【小5算数解説】受験算数 流水算C1:時間差で出発する2 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時3kmの速さで流れている川があります。今、こぐ速さが毎時15kmの水夫が上流のA市から2時間こぎ下ったとき、こぐ速さが毎時9kmの水夫が下流のB市からA市に向かってこぎ上り始めました。B市を出発した水夫は、A市を出発した水夫に何時間後に出会いますか。A市とB市の距離は180kmあります。
この動画を見る
毎時3kmの速さで流れている川があります。今、こぐ速さが毎時15kmの水夫が上流のA市から2時間こぎ下ったとき、こぐ速さが毎時9kmの水夫が下流のB市からA市に向かってこぎ上り始めました。B市を出発した水夫は、A市を出発した水夫に何時間後に出会いますか。A市とB市の距離は180kmあります。
【中学受験問題に挑戦】137(”大人”は頭の体操) 三角形の世界
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
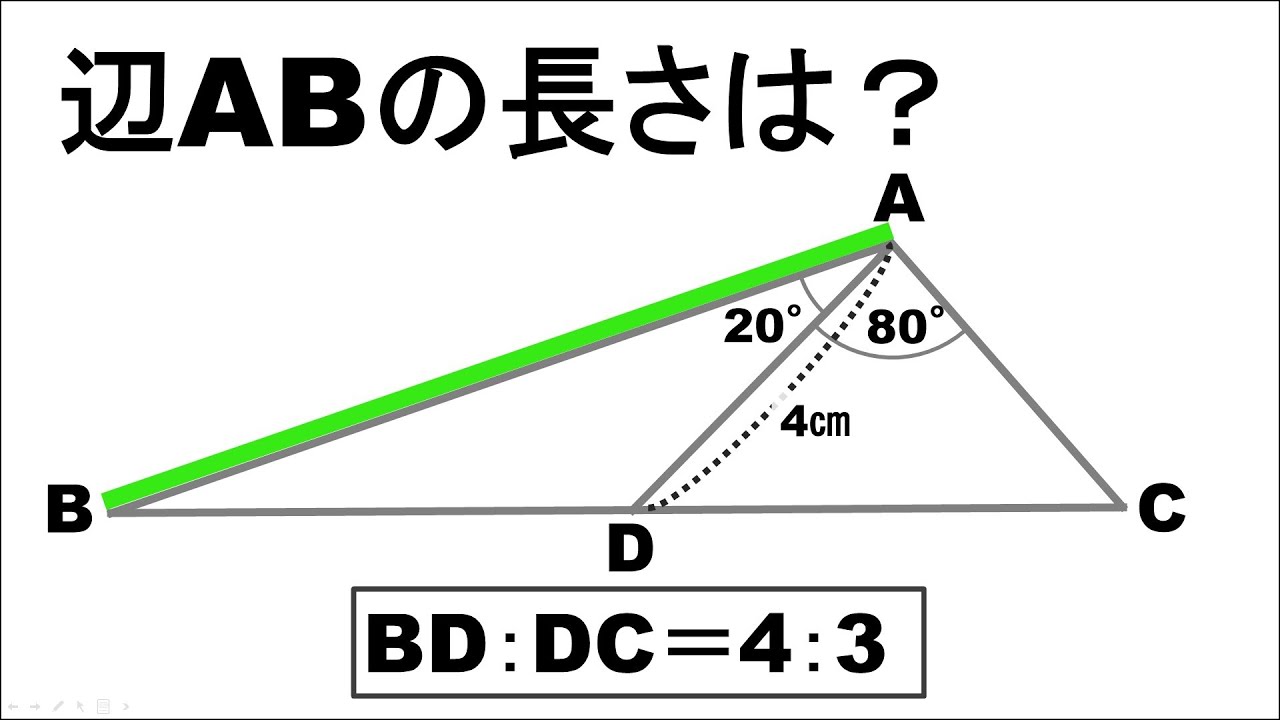
三角形ABCがあり、辺BC上にBD:DC=4:3となる点Dがある
辺ABの長さは?
※図は動画内参照
この動画を見る
三角形ABCがあり、辺BC上にBD:DC=4:3となる点Dがある
辺ABの長さは?
※図は動画内参照
【小5算数解説】受験算数 流水算B4:時間差で出発する1 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時2kmの速さで流れている川をA、B2つの船が、同じ地点から川上に向かって出発します。Aの静水時の速さは毎時12km、Bの静水時の速さは毎時8kmです。Bが出発してから2時間後にAが出発するとき、AがBに追いつくのは、Aが出発してから何時間後ですか。
この動画を見る
毎時2kmの速さで流れている川をA、B2つの船が、同じ地点から川上に向かって出発します。Aの静水時の速さは毎時12km、Bの静水時の速さは毎時8kmです。Bが出発してから2時間後にAが出発するとき、AがBに追いつくのは、Aが出発してから何時間後ですか。
【算数練習】148(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
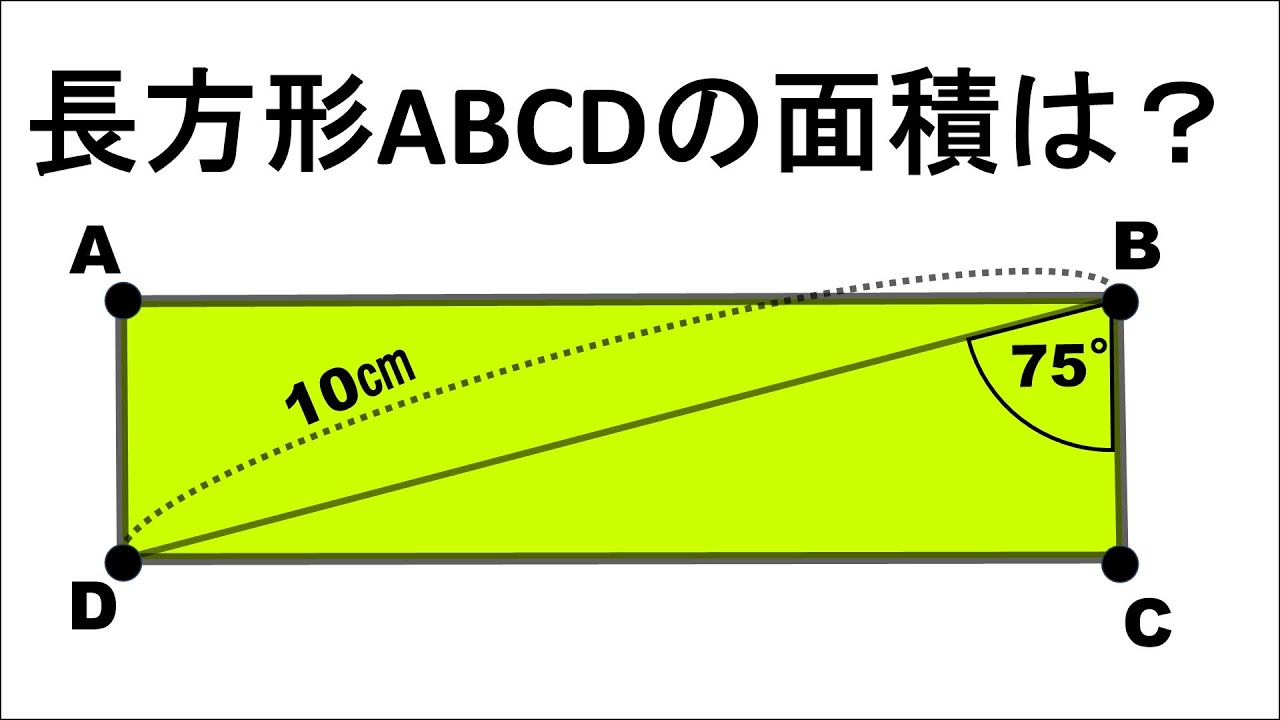
対角線の長さが10㎝の長方形ABCDがある
長方形ABCDの長さは?
※図は動画内参照
この動画を見る
対角線の長さが10㎝の長方形ABCDがある
長方形ABCDの長さは?
※図は動画内参照
【小5算数解説】受験算数 流水算B3:同じ方向に進む2 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A、B2人の水夫がいます。静水をこぐ速さはAが時速5km、Bが時速7kmです。いま、Aは川上から、BはAから48km離れた川下から、向かい合って同時に出発しました。2人がすれ違ってから2時間後に、AはBの出発地点に到着しました。
(1)2人は出発してから何時間後にすれ違いましたか。
(2)この川の流れの速さは時速何kmですか。
この動画を見る
A、B2人の水夫がいます。静水をこぐ速さはAが時速5km、Bが時速7kmです。いま、Aは川上から、BはAから48km離れた川下から、向かい合って同時に出発しました。2人がすれ違ってから2時間後に、AはBの出発地点に到着しました。
(1)2人は出発してから何時間後にすれ違いましたか。
(2)この川の流れの速さは時速何kmですか。
小学生のヤバすぎる発想!感動必至!超おもしろい一題!【中学受験算数】
単元:
#算数(中学受験)#平面図形#角度と面積#平面図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
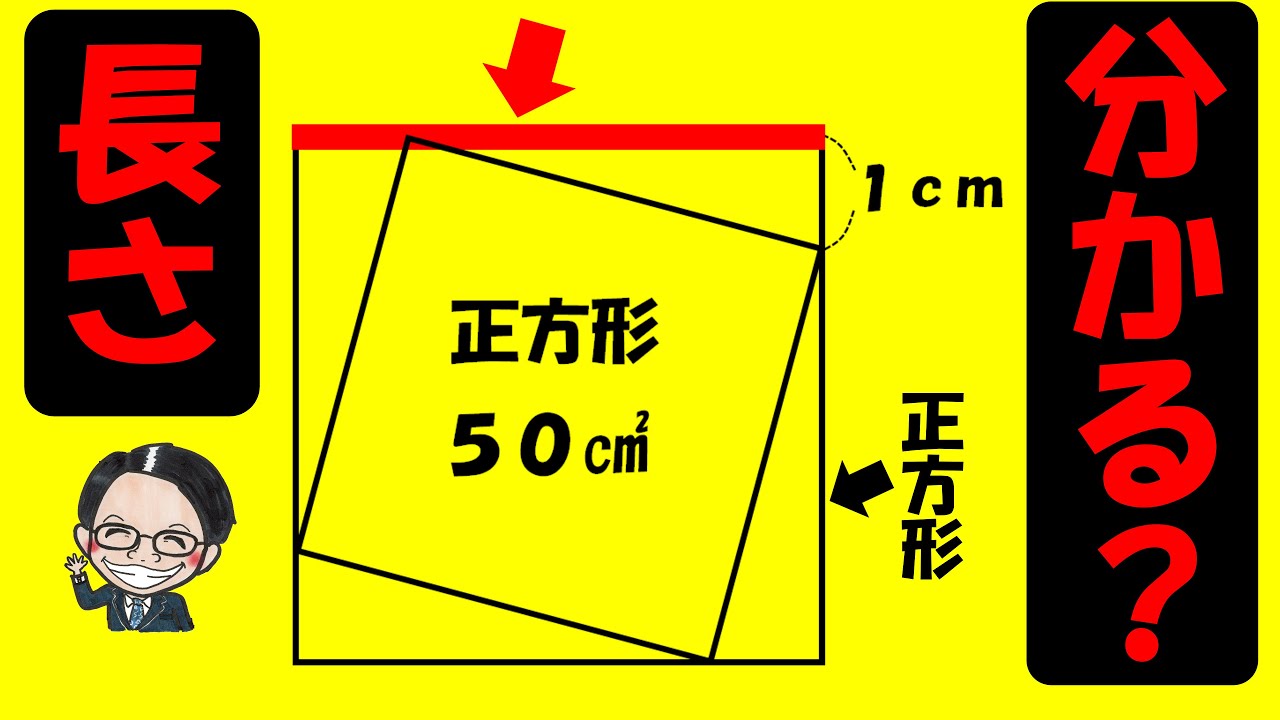
四角形ABCDと四角形EFGHはともに正方形です。
ADは何cm?
図は動画内参照
この動画を見る
四角形ABCDと四角形EFGHはともに正方形です。
ADは何cm?
図は動画内参照
【小5算数解説】受験算数 流水算B2:同じ方向を進む1 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
毎時3kmの速さで流れている川をA、B2つの船が、AはP地点から川上に向かって、BはP地点より48km上流にあるQ地点から川上に向かって同時に出発します。Aの静水時の速さは毎時14km、Bの静水時の速さは毎時10kmです。AがBに追いつくのは、出発してから何時間後ですか。
この動画を見る
毎時3kmの速さで流れている川をA、B2つの船が、AはP地点から川上に向かって、BはP地点より48km上流にあるQ地点から川上に向かって同時に出発します。Aの静水時の速さは毎時14km、Bの静水時の速さは毎時10kmです。AがBに追いつくのは、出発してから何時間後ですか。
【小5算数解説】受験算数 流水算B1:向かい合って進む1 【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
川の上流にあるP町と100km離れた下流のQ町の間をA、B2せきの船が運航しています。川の流れの速さは毎時2.5kmで、船の静水時の速さはAが毎時16km、Bが毎時9kmです。AはP町を、BはQ町を同時に出発するとき、次の問いに答えなさい。
(1)AとBは1時間に何km進みますか。
(2)AとBが初めて出会うのは、出発してから何時間後ですか。
この動画を見る
川の上流にあるP町と100km離れた下流のQ町の間をA、B2せきの船が運航しています。川の流れの速さは毎時2.5kmで、船の静水時の速さはAが毎時16km、Bが毎時9kmです。AはP町を、BはQ町を同時に出発するとき、次の問いに答えなさい。
(1)AとBは1時間に何km進みますか。
(2)AとBが初めて出会うのは、出発してから何時間後ですか。
※右下の角は90°です!!【中学受験問題に挑戦】136(”大人”は頭の体操) 三角形の世界
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
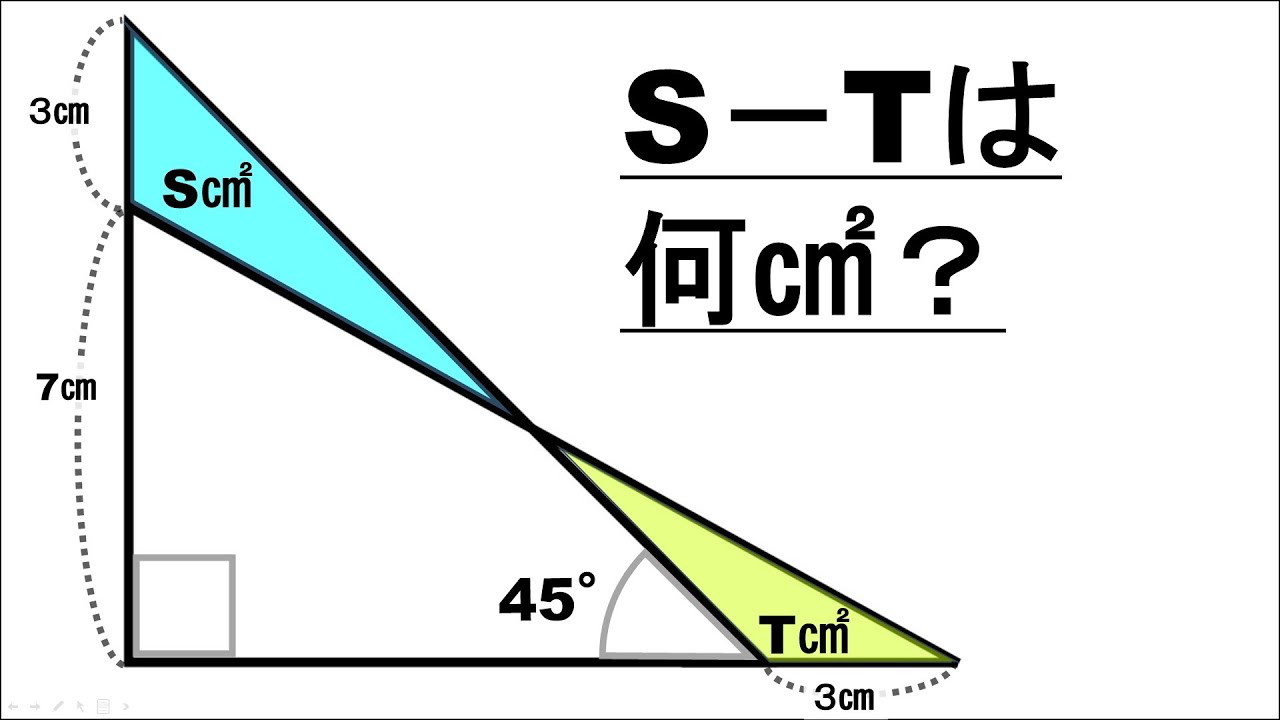
問題文全文(内容文):
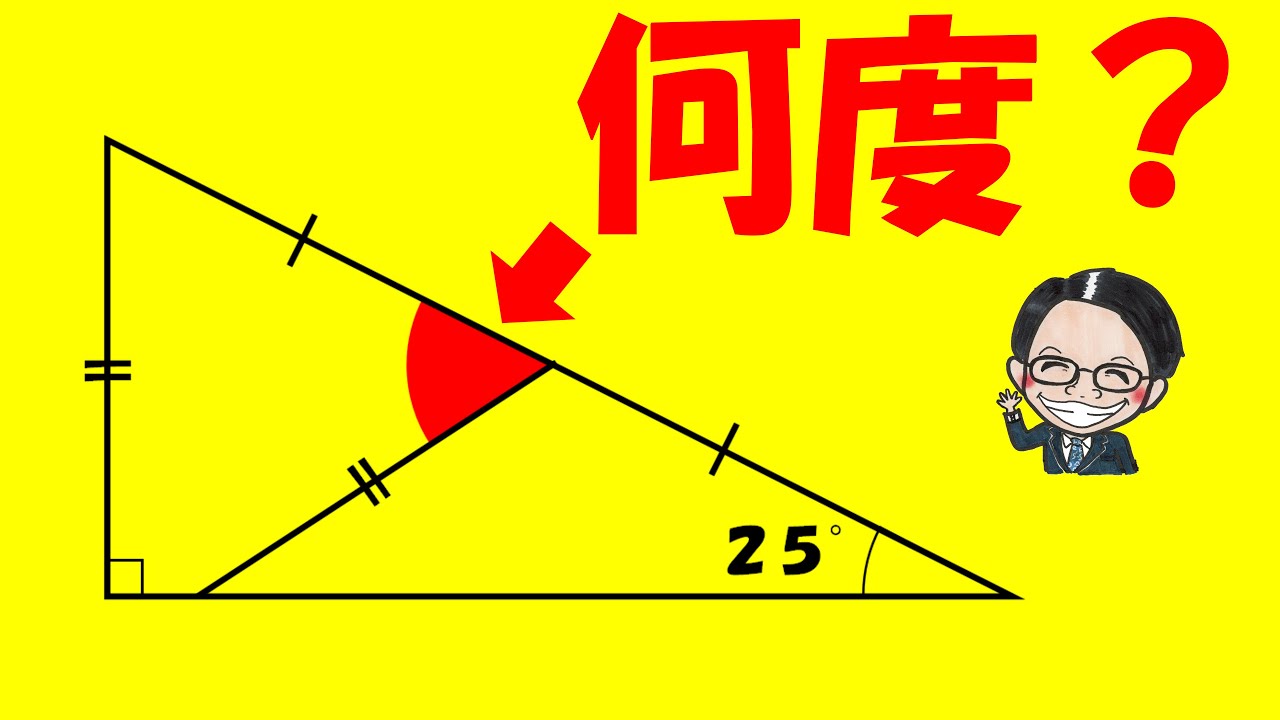
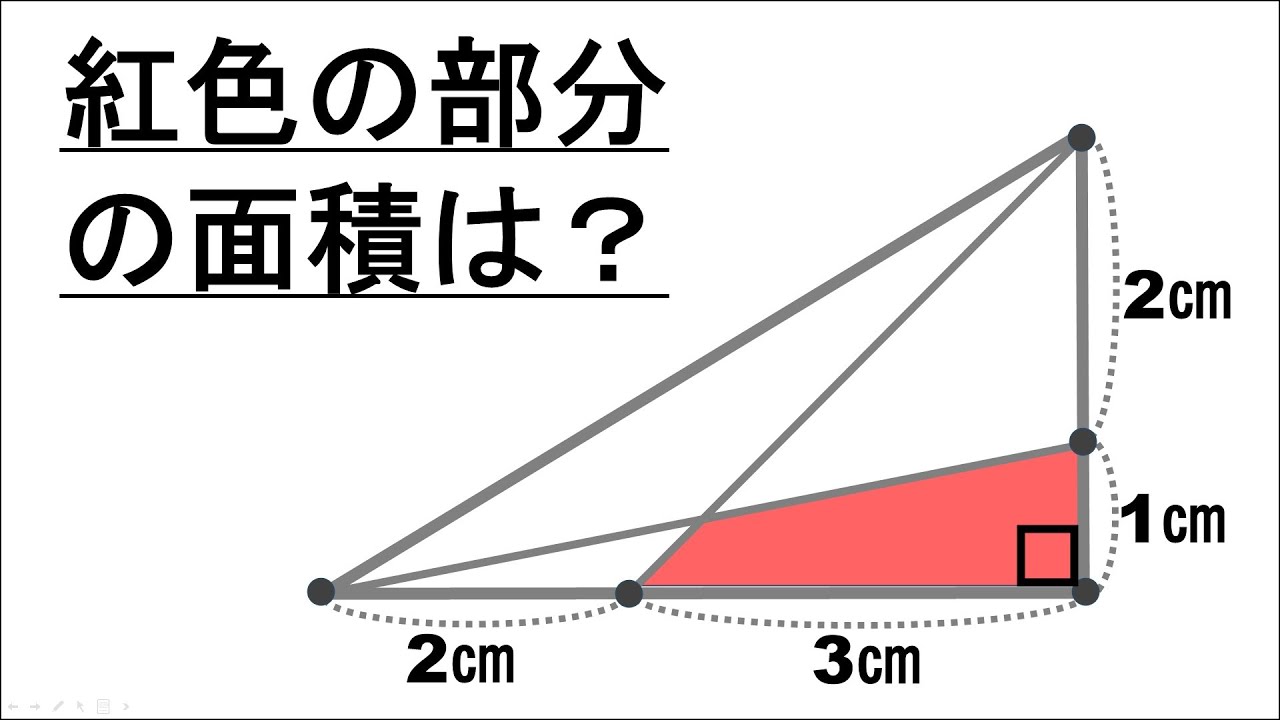
内部に2本直線が引かれた直角三角形がある。
紅色の部分の面積は?
※図は動画内参照
※右下の角は90°です
この動画を見る
内部に2本直線が引かれた直角三角形がある。
紅色の部分の面積は?
※図は動画内参照
※右下の角は90°です
200-1+199=?

【小5算数解説】受験算数 流水算A4:速さが変わる【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
川にそって72kmはなれているA、B2つの町があります。ある船がBを出発してAまで上るのに8時間かかり、下るときは流速が上りのときの2倍となったので、4時間で下ることができました。
(1)この船の上りの速さは時速何kmですか。
(2)流速が2倍になった時の下りの速さは時速何kmですか。
(3)この船の静水時の速さは時速何kmですか。
この動画を見る
川にそって72kmはなれているA、B2つの町があります。ある船がBを出発してAまで上るのに8時間かかり、下るときは流速が上りのときの2倍となったので、4時間で下ることができました。
(1)この船の上りの速さは時速何kmですか。
(2)流速が2倍になった時の下りの速さは時速何kmですか。
(3)この船の静水時の速さは時速何kmですか。
【小5算数解説】受験算数 流水算A3:同じ川を進む【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B2つの船が長さ240kmの川を往復するのに、Aは上りに30時間、下りに20時間かかりました。Bは上りに12時間かかりました。
(1)Aの上りの速さと下りの速さは、それぞれ時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)Bの静水時の速さは時速何kmですか。
(4)この川をBが下るには何時間かかりますか。
この動画を見る
A,B2つの船が長さ240kmの川を往復するのに、Aは上りに30時間、下りに20時間かかりました。Bは上りに12時間かかりました。
(1)Aの上りの速さと下りの速さは、それぞれ時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)Bの静水時の速さは時速何kmですか。
(4)この川をBが下るには何時間かかりますか。
【小5算数解説】受験算数 流水算A2:流水算の基本2【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある水夫が60kmある川を5時間でこぎ上りました。同じところをこぎ下るのに3時間かかりました。
(1)上りの速さは時速何kmですか。
(2)下りの速さは時速何kmですか。
(3)川の流れの速さは時速何kmですか。
(4)静水時の速さは時速何kmですか。
この動画を見る
ある水夫が60kmある川を5時間でこぎ上りました。同じところをこぎ下るのに3時間かかりました。
(1)上りの速さは時速何kmですか。
(2)下りの速さは時速何kmですか。
(3)川の流れの速さは時速何kmですか。
(4)静水時の速さは時速何kmですか。
【算数練習】147(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
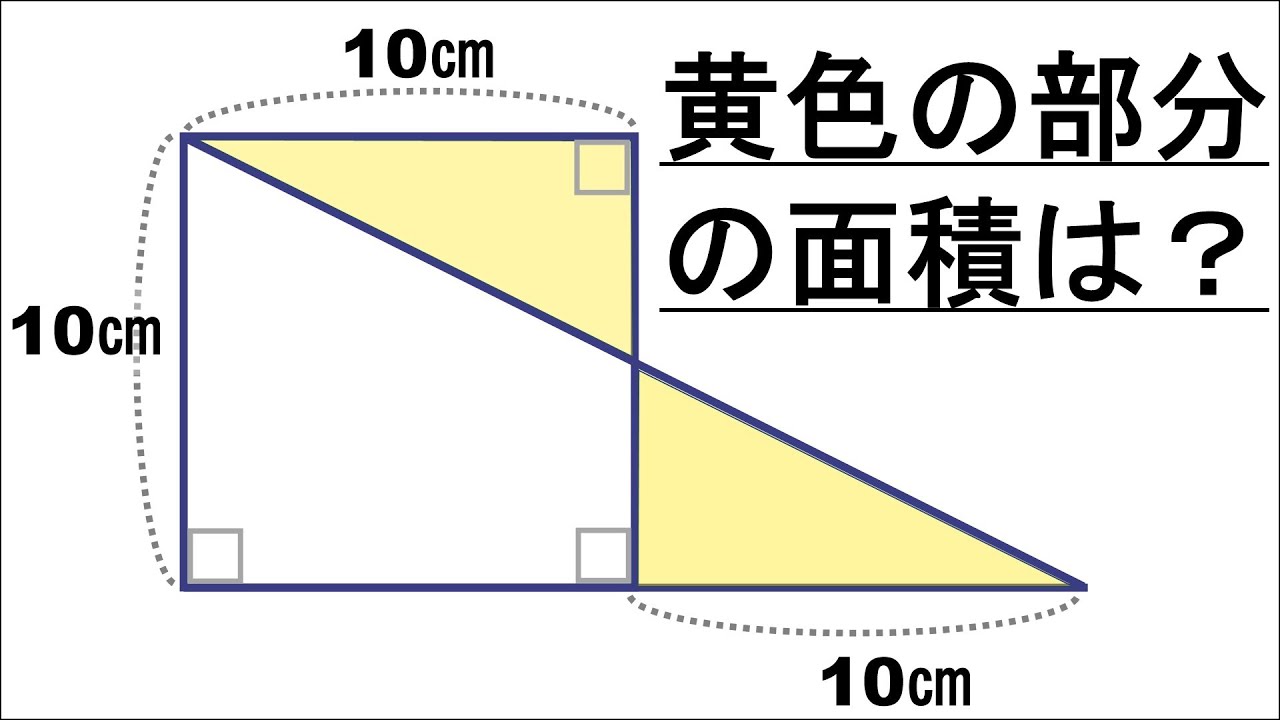
1辺10㎝の正方形と1辺10㎝の三角形が隣接している。
黄色の部分の面積は?
※図は動画内参照
この動画を見る
1辺10㎝の正方形と1辺10㎝の三角形が隣接している。
黄色の部分の面積は?
※図は動画内参照
すごい発想!やわらか頭になれるかな?【中学受験算数】

【小5算数解説】受験算数 流水算A1:流水算の基本1【問題文は概要欄】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#SPX#5年算数D-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
流れのないところを時速 14 kmで進む船が,ある川を5時間で80㎞下りました。
(1)この川を下るときの速さは時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)この川を上るときの速さは時速何kmですか。
(4)この川を2時間上るとき、何km進みますか
この動画を見る
流れのないところを時速 14 kmで進む船が,ある川を5時間で80㎞下りました。
(1)この川を下るときの速さは時速何kmですか。
(2)この川の流れの速さは時速何kmですか。
(3)この川を上るときの速さは時速何kmですか。
(4)この川を2時間上るとき、何km進みますか
【算数練習】146(”大人”は頭の体操)
単元:
#算数(中学受験)#平面図形#角度と面積#図形の移動#平面図形その他
指導講師:
算数・数学ちゃんねる
問題文全文(内容文):
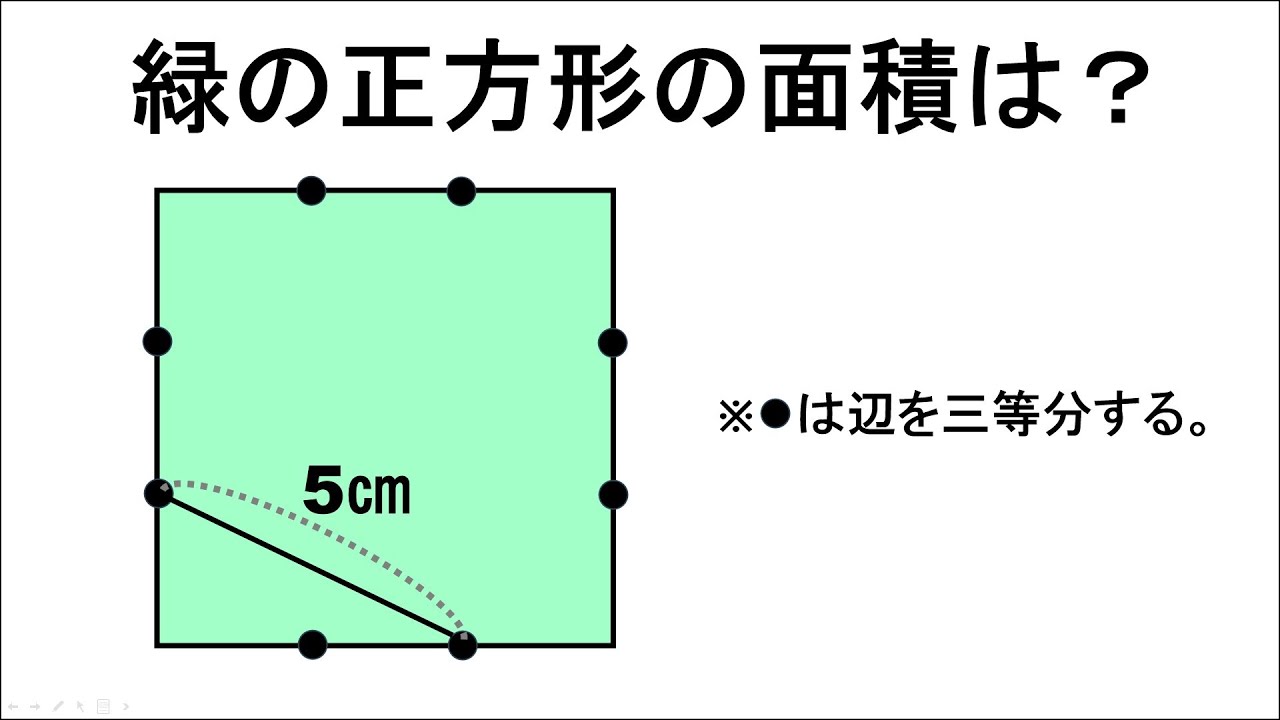
緑の正方形の面積は?
※●は辺を三等分する
※図は動画内参照
この動画を見る
緑の正方形の面積は?
※●は辺を三等分する
※図は動画内参照
