 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
ざ・算数

中学受験算数「割合⑤(円グラフ)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第15回割合⑤(円グラフ)
例題下の円グラフは、ある学校の通学地域別の人数の 割合を表したものです。
(1)この学校の生徒数は何人ですか。
(2) C市から通学している生徒は何人ですか。
(3) B市の部分のおうぎ形の中心角は何度 ですか。
この動画を見る
第15回割合⑤(円グラフ)
例題下の円グラフは、ある学校の通学地域別の人数の 割合を表したものです。
(1)この学校の生徒数は何人ですか。
(2) C市から通学している生徒は何人ですか。
(3) B市の部分のおうぎ形の中心角は何度 ですか。
簡単に解けそうで意外に解けない難問!解くためのたった1つのカギは○○【中学受験算数】【入試問題】【中央大学附属中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#中央大学附属中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021帝京大学中学校
上図の正六角形で、㋐は何度?
2021桐光学園中学校
上図の四角形ABCDは平行四辺形です。
(1)三角形AEGと三角形DGCの面積比は?
(2)AG:GHは?
(3)四角形ABCDが120㎠のとき、四角形GEFHの面積は?
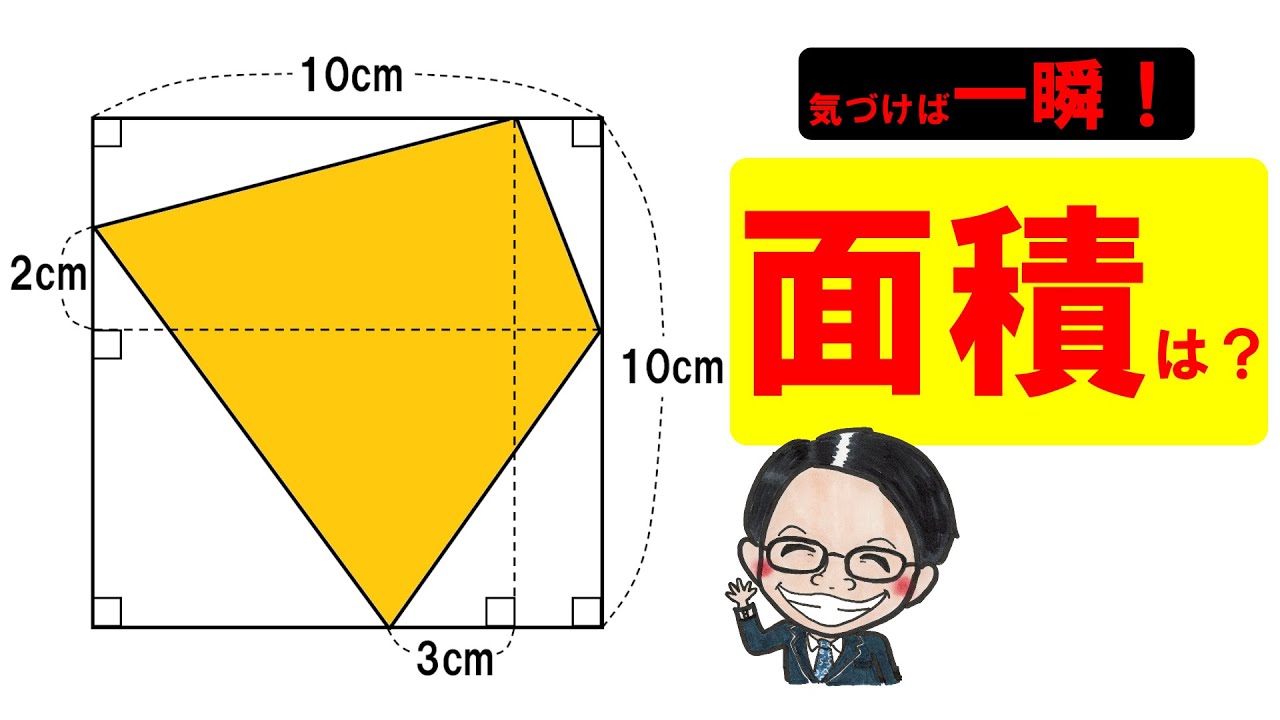
2021中央大学附属中学校
左図の四角形ABCDの面積は?
*図は動画内参照
この動画を見る
2021帝京大学中学校
上図の正六角形で、㋐は何度?
2021桐光学園中学校
上図の四角形ABCDは平行四辺形です。
(1)三角形AEGと三角形DGCの面積比は?
(2)AG:GHは?
(3)四角形ABCDが120㎠のとき、四角形GEFHの面積は?
2021中央大学附属中学校
左図の四角形ABCDの面積は?
*図は動画内参照
中学受験算数「割合④(帯グラフ)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第15回割合 ④(帯グラフ)
例題下のグラフは、ある地区の土地利用のようすを表したものです。
(1) 畑の割合は、全体の何%ですか。
(2)このグラフ全体の長さを30cmとすると、山林部分の長さは何cmになりますか。
(3)この地区の土地全体の面積が160㎡のとき、田の面積は何がですか。
(4) 畑の面積が70kmのとき、この地区の土地全体の面積は何ですか。
この動画を見る
第15回割合 ④(帯グラフ)
例題下のグラフは、ある地区の土地利用のようすを表したものです。
(1) 畑の割合は、全体の何%ですか。
(2)このグラフ全体の長さを30cmとすると、山林部分の長さは何cmになりますか。
(3)この地区の土地全体の面積が160㎡のとき、田の面積は何がですか。
(4) 畑の面積が70kmのとき、この地区の土地全体の面積は何ですか。
中学受験算数「植木算⑤(リング問題)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第2回植木算⑤(リング問題)
例題
図1のようなリングを、図2のようにつないでいきます。
(1)このリングを10個つないだとき、端から端までの長さは何センチになりますか?
(2) はしからはしまでの長さが110cmになるのは、このリングを 何個つないだときですか。
この動画を見る
第2回植木算⑤(リング問題)
例題
図1のようなリングを、図2のようにつないでいきます。
(1)このリングを10個つないだとき、端から端までの長さは何センチになりますか?
(2) はしからはしまでの長さが110cmになるのは、このリングを 何個つないだときですか。
【受験算数】立体切断演習問題その4「切断面を伸ばして考える2」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
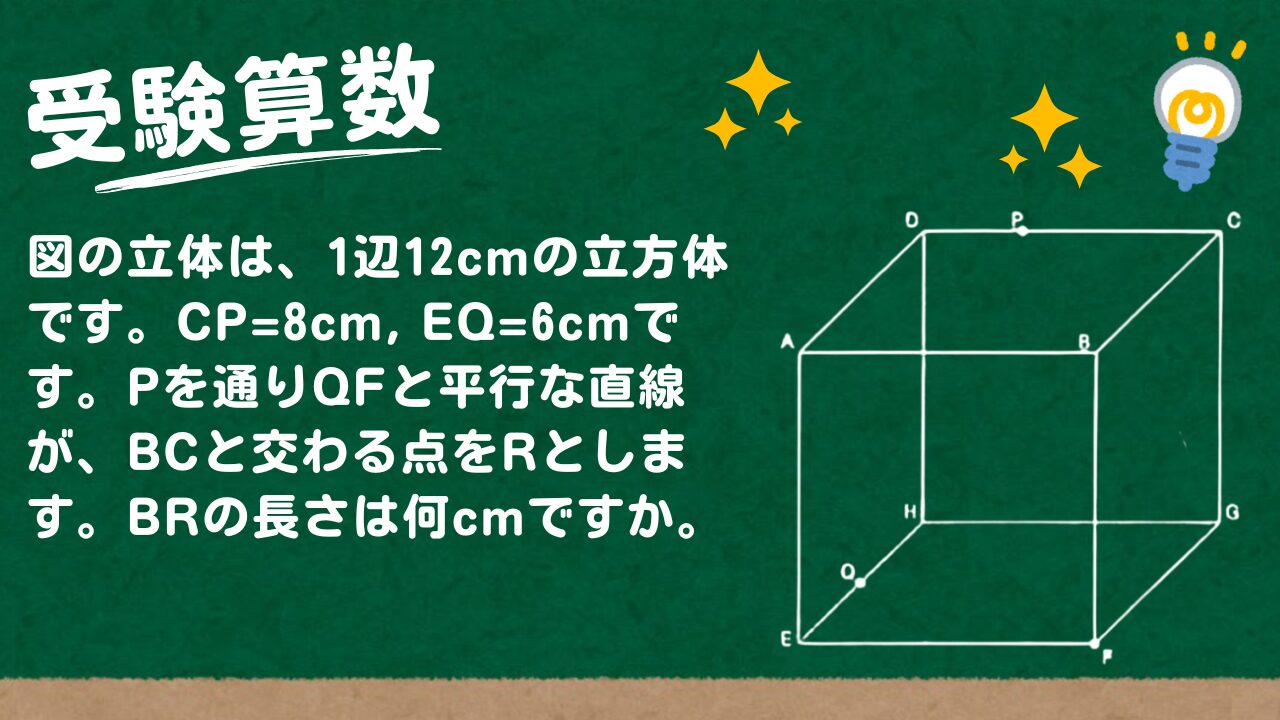
下の図の立体は、1辺12cmの立方体です。CP=8cm, EQ=6cmです。
(1) Pを通りQFと平行な直線が、BCと交わる点をRとします。BRの長さは何cmですか。
この動画を見る
下の図の立体は、1辺12cmの立方体です。CP=8cm, EQ=6cmです。
(1) Pを通りQFと平行な直線が、BCと交わる点をRとします。BRの長さは何cmですか。
【受験算数】立体切断演習問題その3「切断面を伸ばして考える1」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
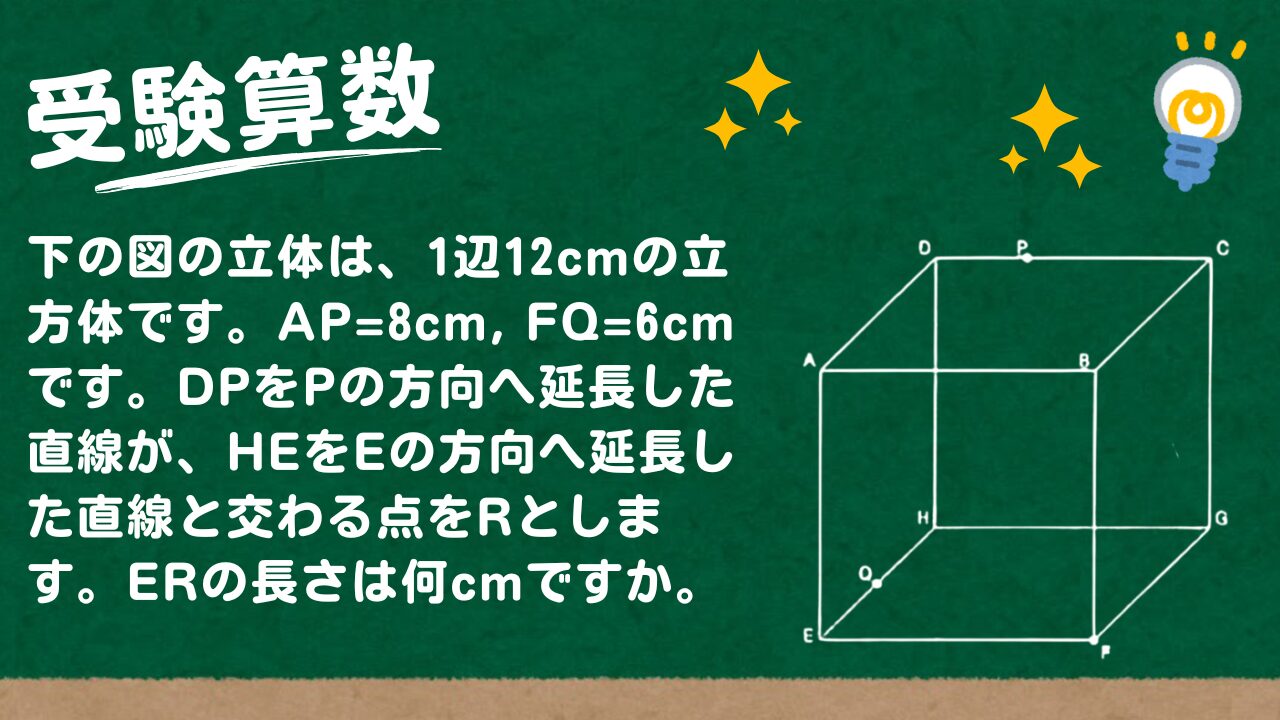
下の図の立体は、1辺12cmの立方体です。AP=8cm, FQ=6cmです。
(1) DPをPの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をRとします。ERの長さは何cmですか。
この動画を見る
下の図の立体は、1辺12cmの立方体です。AP=8cm, FQ=6cmです。
(1) DPをPの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をRとします。ERの長さは何cmですか。
感動!この問題の答えが美しすぎる!超気持ちいい良問!【集合体恐怖症の方は閲覧注意】【中学受験算数】【入試問題】【帝京大学中】
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
2021日本大学中学校
直角三角形ABCを、Cを中心として90°回転させたとき、太線内の面積は?
2021成蹊中学校
1辺が12cmの正方形ABCDの中に、点B、点Cのそれぞれを中心とする半径12cmの
円の一部をかき、さらに対角線ACをかく。
このとき,
(1)㋐の部分の周の長さは?
(2)㋐と㋑の部分の面積差は?
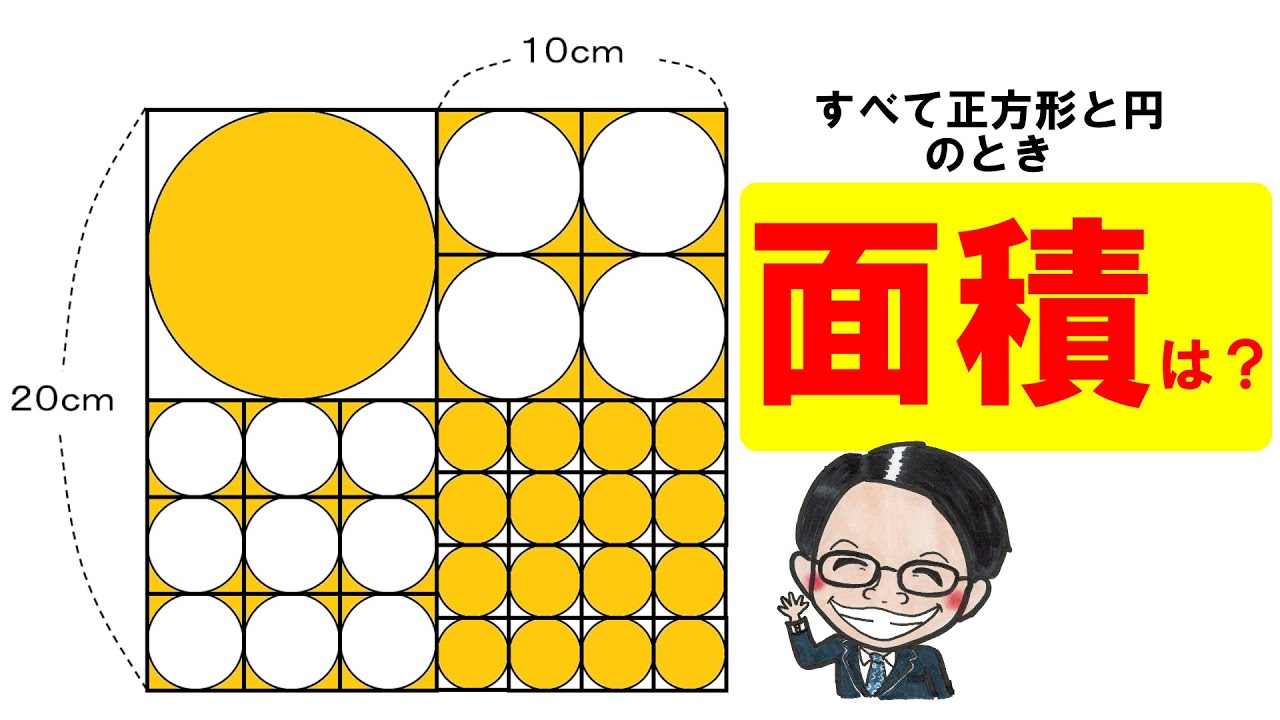
2021帝京大学中学校
左図は正方形と円を組み合わせた図形です。斜線部分の面積は?
(円周率は3.14)
*図は動画内参照
この動画を見る
2021日本大学中学校
直角三角形ABCを、Cを中心として90°回転させたとき、太線内の面積は?
2021成蹊中学校
1辺が12cmの正方形ABCDの中に、点B、点Cのそれぞれを中心とする半径12cmの
円の一部をかき、さらに対角線ACをかく。
このとき,
(1)㋐の部分の周の長さは?
(2)㋐と㋑の部分の面積差は?
2021帝京大学中学校
左図は正方形と円を組み合わせた図形です。斜線部分の面積は?
(円周率は3.14)
*図は動画内参照
これ説明できる?

中学受験算数「植木算④(のりしろ②)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第2回植木算④(のりしろ②)
例題 長さ8cmのテープを、のりしろが1cmになるようにして つな げたところ、 全体の長さが106cmになりました。 テープを何枚つなげましたか。
この動画を見る
第2回植木算④(のりしろ②)
例題 長さ8cmのテープを、のりしろが1cmになるようにして つな げたところ、 全体の長さが106cmになりました。 テープを何枚つなげましたか。
これは知らなきゃ損

【受験算数】立体切断演習問題その2「基本ルールを確認しながら解きましょう2」

単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1から図6の立体は、すべて1辺4cmの立方体です。図1の3つの点C、D、Eを通る平面で切断すると、その切断は図1に示したようになり、その形は長方形です。図2から図6の立方体を、それぞれの示された3つの点を通る平面で切断すると、その切断面はどのようになりますか。それぞれの図にかきこみ、図のように斜線をつけなさい。また、それはどのような形ですか。それぞれ、最もふさわしい図形の名前を答えなさい。
この動画を見る
図1から図6の立体は、すべて1辺4cmの立方体です。図1の3つの点C、D、Eを通る平面で切断すると、その切断は図1に示したようになり、その形は長方形です。図2から図6の立方体を、それぞれの示された3つの点を通る平面で切断すると、その切断面はどのようになりますか。それぞれの図にかきこみ、図のように斜線をつけなさい。また、それはどのような形ですか。それぞれ、最もふさわしい図形の名前を答えなさい。
【受験算数】立体切断演習問題その1「基本ルールを確認しながら解きましょう」
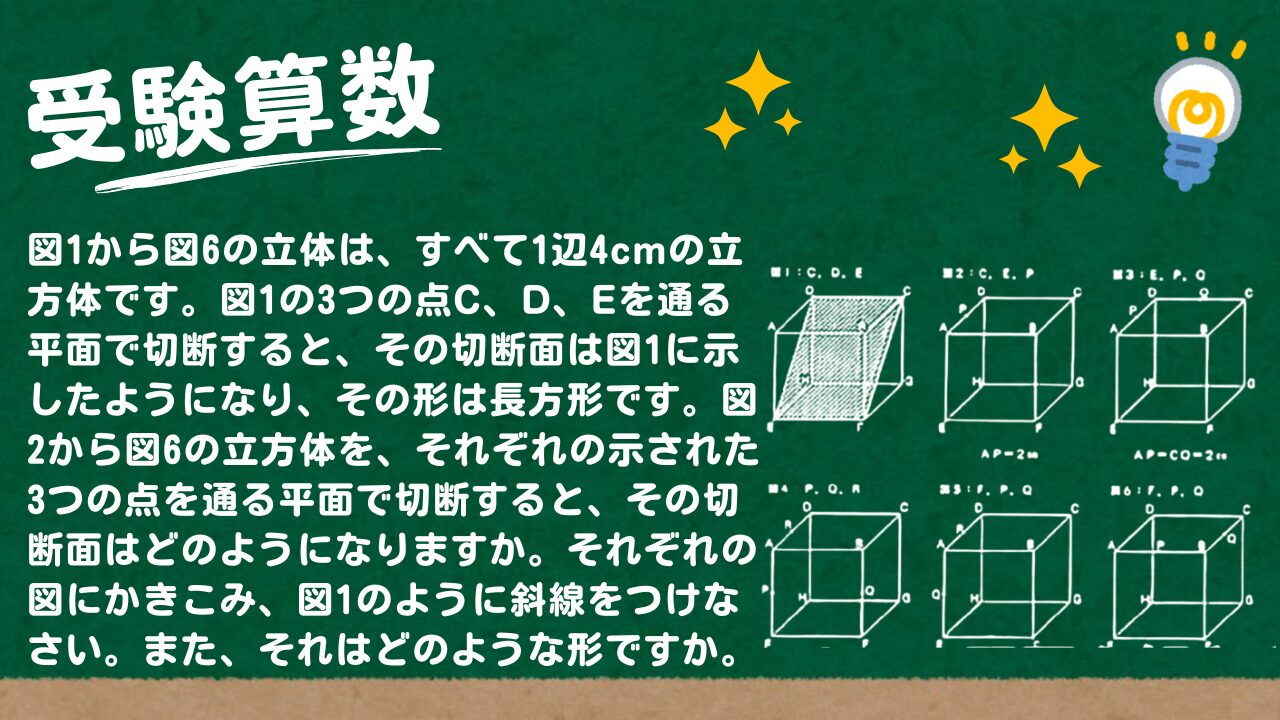
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図1から図6の立体は、すべて1辺4cmの立方体です。図1の3つの点C、D、 Eを通る平面で切断すると、その切断面は図1に示したようになり、その形は長方形です。図2から図6の立方体を、それぞれの示された3つの点を通る平面で切断すると、その切断面はどのようになりますか。それぞれの図にかきこみ、図1のように斜線をつけなさい。また、それはどのような形ですか。それぞれ、最もふさわしい図形の名前を答えなさい。
この動画を見る
図1から図6の立体は、すべて1辺4cmの立方体です。図1の3つの点C、D、 Eを通る平面で切断すると、その切断面は図1に示したようになり、その形は長方形です。図2から図6の立方体を、それぞれの示された3つの点を通る平面で切断すると、その切断面はどのようになりますか。それぞれの図にかきこみ、図1のように斜線をつけなさい。また、それはどのような形ですか。それぞれ、最もふさわしい図形の名前を答えなさい。
【受験算数】立体切断の基本「3つの手順」

中学受験算数「植木算③(のりしろ①)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第2回植木算③(のりしろ①)
例1長さ10cmのテープを、のりしろを2cmずつとって20枚つなげると 全体の長さは何cmになりますか。
例2のりしろをすべて同じ長さにして、長さ8cmのテープ35枚をつなげると 全体の長さは212cmになりました。のりしろ1つの長さは何cmですか。
例3 長さ19cmのテープ11枚をのりしろ1cmにして、輪になるようにつなぎました。この輪の周りの長さは何cmですか。
この動画を見る
第2回植木算③(のりしろ①)
例1長さ10cmのテープを、のりしろを2cmずつとって20枚つなげると 全体の長さは何cmになりますか。
例2のりしろをすべて同じ長さにして、長さ8cmのテープ35枚をつなげると 全体の長さは212cmになりました。のりしろ1つの長さは何cmですか。
例3 長さ19cmのテープ11枚をのりしろ1cmにして、輪になるようにつなぎました。この輪の周りの長さは何cmですか。
これ説明できる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記の問題を解け
$7 \times 7 \div 7 \times 7$
この動画を見る
下記の問題を解け
$7 \times 7 \div 7 \times 7$
これ思いつくのすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$(975+319+753+197+531) \div 5$
この動画を見る
$(975+319+753+197+531) \div 5$
反則技を使わないと解けませんでした!小学生の知識のみで解ける方法が分かった方は教えてください。【中学受験算数】【入試問題】【筑波大学附属中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#筑波大学附属中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021青稜中学校
左図で、四角形ABCDと四角形EFGHは長方形です。
このとき四角形EFGHの面積は?
2021専修大学松戸中学校
(1)AD:BC=__:__
(2)AE:EB=__:__
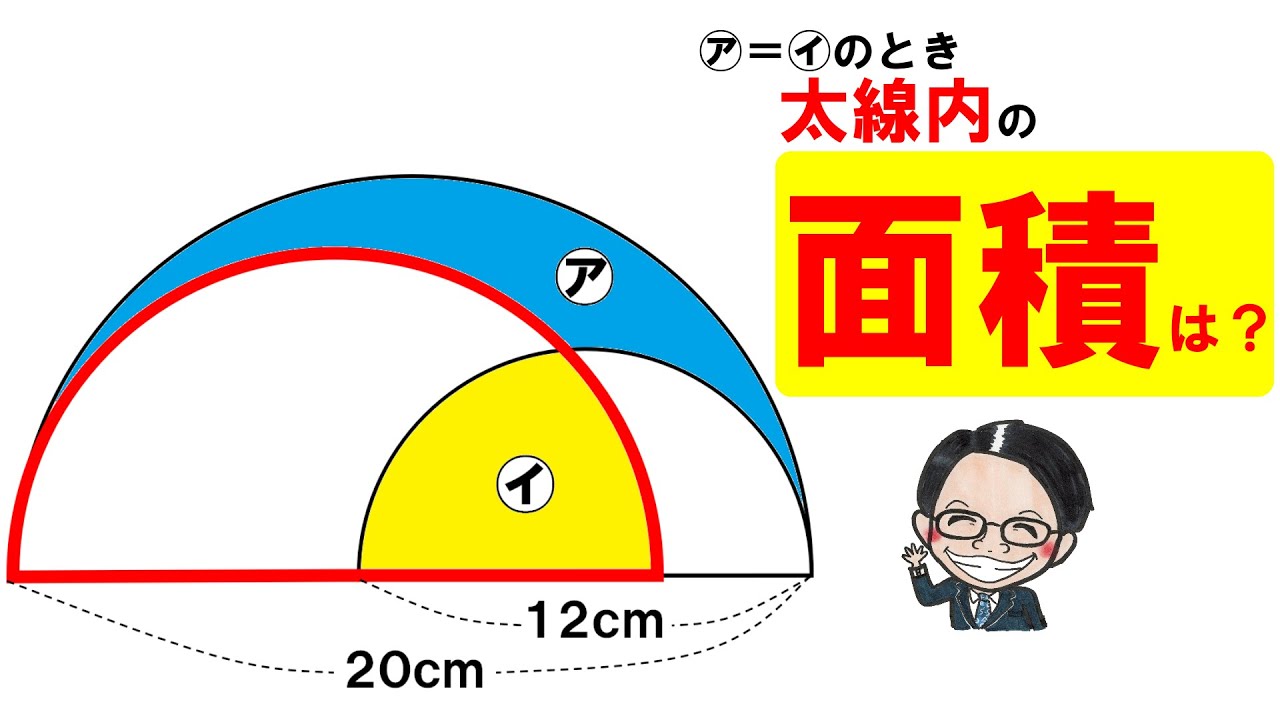
2021筑波大学附属中学校
[大][中][小]の3つの半円を左図のように重ねると、㋐と㋑の面積が等しかった。このとき[中]の半円の面積は?
*図は動画内参照
この動画を見る
2021青稜中学校
左図で、四角形ABCDと四角形EFGHは長方形です。
このとき四角形EFGHの面積は?
2021専修大学松戸中学校
(1)AD:BC=__:__
(2)AE:EB=__:__
2021筑波大学附属中学校
[大][中][小]の3つの半円を左図のように重ねると、㋐と㋑の面積が等しかった。このとき[中]の半円の面積は?
*図は動画内参照
中学受験算数「日暦算③(過去の曜日)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第4回 日曆算③
例1 ある年の6月6日は土曜日です。 この年の5月3日は何曜日ですか。
例2 ある年の10月15日は水曜日です。 この年の6月17日は何曜日ですか。
この動画を見る
第4回 日曆算③
例1 ある年の6月6日は土曜日です。 この年の5月3日は何曜日ですか。
例2 ある年の10月15日は水曜日です。 この年の6月17日は何曜日ですか。
え!?これだけの情報で解けるの?実は○○を使えば解けるんです!さあ、あなたは解けるかな?【中学受験算数】【入試問題】【西大和学園中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#豊島岡女子学園中学#西大和学園中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022豊島岡女子学園中学校
左図の正方形ABCDで斜線部分の面積は?
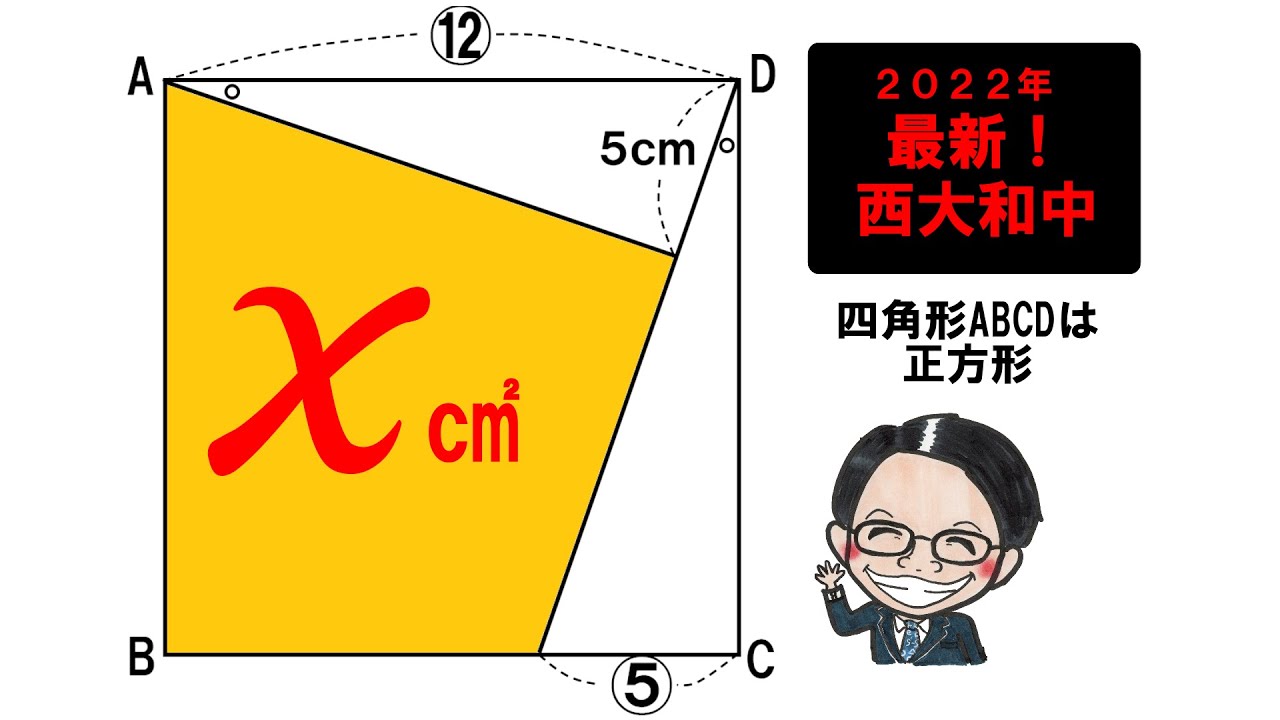
2022西大和学園中学校
左図の四角形ABCDは正方形で、(ADの長さ):(CEの長さ)=12:5となるように辺BC上に点Eをとる。図の○のついた角の大きさが同じになるようにDE上に点FをとったとこりDFの長さが5㎝となった。
四角形ABEFの面積は?
*図は動画内参照
この動画を見る
2022豊島岡女子学園中学校
左図の正方形ABCDで斜線部分の面積は?
2022西大和学園中学校
左図の四角形ABCDは正方形で、(ADの長さ):(CEの長さ)=12:5となるように辺BC上に点Eをとる。図の○のついた角の大きさが同じになるようにDE上に点FをとったとこりDFの長さが5㎝となった。
四角形ABEFの面積は?
*図は動画内参照
【作り方を覚えて暗記量を減らす!?】半反応式の作り方〔現役塾講師解説、高校化学、化学基礎〕

単元:
#計算と数の性質#化学#化学基礎2ー物質の変化#化学変化と化学反応式#理科(高校生)
指導講師:
3rd School
問題文全文(内容文):
化学基礎
半反応式の作り方について解説します。
この動画を見る
化学基礎
半反応式の作り方について解説します。
中学受験算数「速さのグラフ(ダイヤグラム)④」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#速さ#ダイヤグラム
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第58回速さのグラフ(ダイヤグラム) ④
例題
坂の上で3分間休んだあと、同じ道を分速80mで下ったら、 出発してから42分後に出発点にもどってきました。
次のグラフは、そのときのようすを表したものです。
(1)アにあてはまる数を求めなさい。
(2)この坂道は何mありますか。
この動画を見る
第58回速さのグラフ(ダイヤグラム) ④
例題
坂の上で3分間休んだあと、同じ道を分速80mで下ったら、 出発してから42分後に出発点にもどってきました。
次のグラフは、そのときのようすを表したものです。
(1)アにあてはまる数を求めなさい。
(2)この坂道は何mありますか。
中学受験算数「速さのグラフ(ダイヤグラム)③」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#速さ#ダイヤグラム
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第58回速さのグラフ(ダイヤグラム)③
例題 3600mはなれたP地とQ地があります。弟は、午前8時に P地を歩いて出発し、Q地に向かいました。兄は、弟より おくれてQ地を自転車で出発し、8時20分にP地に着き ました。地に着いてすぐに、行きと同じ速さでQ地に 向かいましたが、途中で自転車が故障してしまったので、 歩いて行ったところ、Q地にもどったのは、8時42分でした。 弟も兄も歩く速さは分速80mで、自転車の速さは一定で あるとします。次のグラフは、そのときのようすを表したものです。
(1)8時15分に、弟はP地から何mはなれた ところにいましたか。
(2) 自転車の速さは、分速何ですか。
(3) P地で折り返した兄が、弟を追いこしたのは、 8時何分ですか。
この動画を見る
第58回速さのグラフ(ダイヤグラム)③
例題 3600mはなれたP地とQ地があります。弟は、午前8時に P地を歩いて出発し、Q地に向かいました。兄は、弟より おくれてQ地を自転車で出発し、8時20分にP地に着き ました。地に着いてすぐに、行きと同じ速さでQ地に 向かいましたが、途中で自転車が故障してしまったので、 歩いて行ったところ、Q地にもどったのは、8時42分でした。 弟も兄も歩く速さは分速80mで、自転車の速さは一定で あるとします。次のグラフは、そのときのようすを表したものです。
(1)8時15分に、弟はP地から何mはなれた ところにいましたか。
(2) 自転車の速さは、分速何ですか。
(3) P地で折り返した兄が、弟を追いこしたのは、 8時何分ですか。
福田の数学〜慶應義塾大学2022年薬学部第1問(7)〜直三角柱の切断面の面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形の性質#微分法と積分法#学校別大学入試過去問解説(数学)#立体図形#立体切断#空間における垂直と平行と多面体(オイラーの法則)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
この動画を見る
(7)1辺の長さが$\sqrt2$の正三角形を底面とし、高さが4の直三角柱を考える。
この直三角柱を以下の条件①と条件②を共に満たす平面で切断するとき、切断面の
面積の最小値は$\boxed{\ \ シ\ \ }$である。ただし、直三角柱は底面と側面が垂直である三角柱
のことである。
条件① 切断面が直角三角形になる。
条件② 切断面の図形のすべての辺が直三角柱の側面上にある。
2022慶應義塾大学薬学部過去問
中学受験算数「速さのグラフ*基本編②(ダイヤグラム)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#速さ#ダイヤグラム
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第58回速さのグラフ※基本編②
例題
Aさんは、家から1800mはなれた公園に行きました。 9時15分に歩いて自宅を出発しました。
しかし、忘れ物に気づき、同じ速さで家にもどりました。 家で忘れ物を探して見つけたあと、分速150mの速さで自転車に乗って、 公園に向かったところ、9時40分に公園に着きました。 次のグラフは、Aさんが家を出発してから公園に着くまでのようすを表したものです。
(1) Aさんの歩く速さは、分速何mですか。
(2) グラフのアの時こくは、9時何分ですか。
(3) 忘れ物を探していた時間は、何分間ですか。
この動画を見る
第58回速さのグラフ※基本編②
例題
Aさんは、家から1800mはなれた公園に行きました。 9時15分に歩いて自宅を出発しました。
しかし、忘れ物に気づき、同じ速さで家にもどりました。 家で忘れ物を探して見つけたあと、分速150mの速さで自転車に乗って、 公園に向かったところ、9時40分に公園に着きました。 次のグラフは、Aさんが家を出発してから公園に着くまでのようすを表したものです。
(1) Aさんの歩く速さは、分速何mですか。
(2) グラフのアの時こくは、9時何分ですか。
(3) 忘れ物を探していた時間は、何分間ですか。
中学受験算数「速さのグラフ*基本編①(ダイヤグラム)」小学4年生~6年生対象

単元:
#算数(中学受験)#速さ#ダイヤグラム
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
次のグラフは、けいこさんが家から駅まで自転車で行ったときのようすを表したものです。
家からはじめは分速180mで進み、途中、図書館で15分間調べものをしました。
その後、図書館からは分速200mで駅に向かい、家を出てから50分後駅に着きました。
(1) 家から図書館までは、何mありますか。
(2) 図書館から駅までは、何mありますか。
(3) 帰りは、駅から家までは、行きと同じ道を一定の速さで休まずに走って40分かかりました。
帰りの自転車の速さは、分速何mですか。
この動画を見る
次のグラフは、けいこさんが家から駅まで自転車で行ったときのようすを表したものです。
家からはじめは分速180mで進み、途中、図書館で15分間調べものをしました。
その後、図書館からは分速200mで駅に向かい、家を出てから50分後駅に着きました。
(1) 家から図書館までは、何mありますか。
(2) 図書館から駅までは、何mありますか。
(3) 帰りは、駅から家までは、行きと同じ道を一定の速さで休まずに走って40分かかりました。
帰りの自転車の速さは、分速何mですか。
簡単そう?麻布中の問題です!たぶんコレが一番簡単な解き方!特殊な時計算も解説するよ!【中学受験算数】【入試問題】【麻布中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#速さ#点の移動・時計算#麻布中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022麻布中学校
2時から3時までの1時間で、左図の点線と短針の間の角度が、長針によって2等分される時刻は?
(ただし、秒の値のみ帯分数で答えこと)
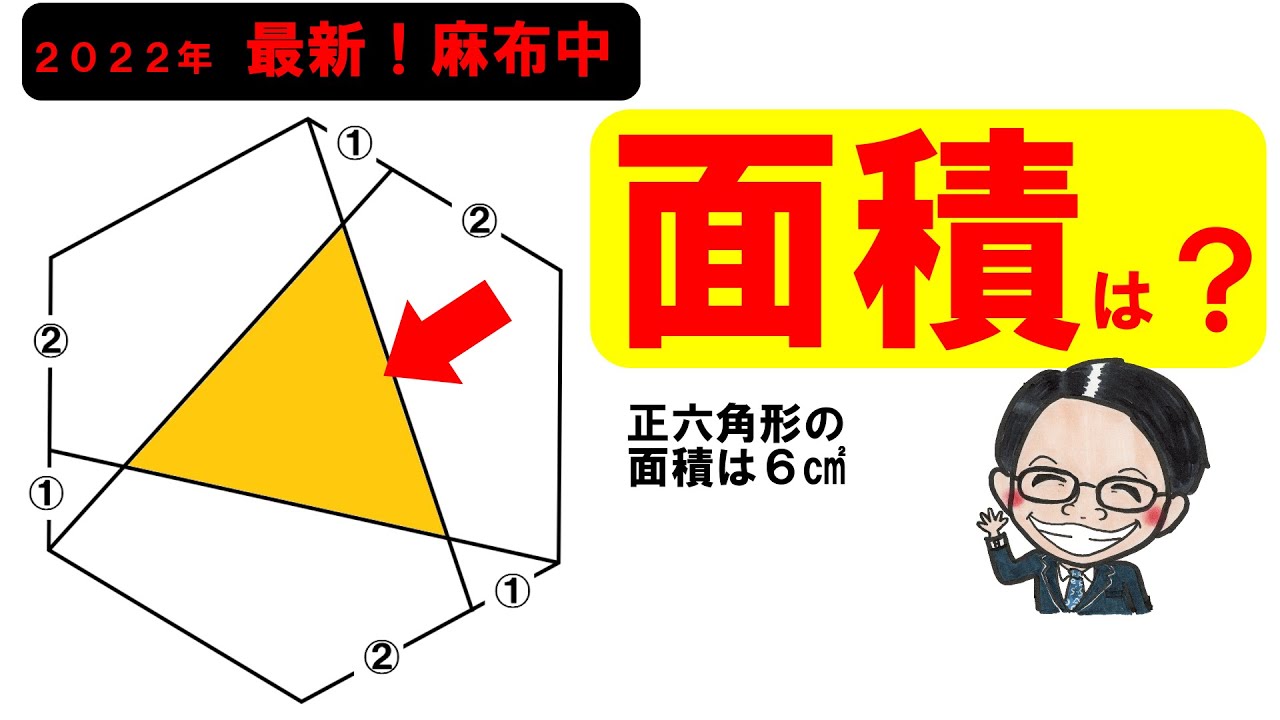
2022麻布中学校
左図のような面積が6㎠の正六角形で、(1)~(3)は?
(1)三角形ACGの面積は__㎠です
(2)三角形AJGの面積は__㎠です
(3)三角形JKLの面積は__㎠です
*図は動画内参照
この動画を見る
2022麻布中学校
2時から3時までの1時間で、左図の点線と短針の間の角度が、長針によって2等分される時刻は?
(ただし、秒の値のみ帯分数で答えこと)
2022麻布中学校
左図のような面積が6㎠の正六角形で、(1)~(3)は?
(1)三角形ACGの面積は__㎠です
(2)三角形AJGの面積は__㎠です
(3)三角形JKLの面積は__㎠です
*図は動画内参照
中学受験算数「速さのグラフ*基本編①(ダイヤグラム)」小学4年生~6年生対象【毎日配信】

単元:
#算数(中学受験)#速さ#ダイヤグラム
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
第58回速さのグラフ ※基本編① ―
例題
次のグラフは、けいこさんが家から駅まで自転車で行ったときのようすを 表したものです。
家からはじめは分速180mで進み、途中、図書館で 15分間調べものをしました。
その後、図書館からは分速200mで向かい、家を出てから50分後に駅に着きました。
(1)家から図書館までは、何mありますか。
(2) 図書館から駅までは、何mありますか。
(3)帰りは、駅から家までは、行きと同じ道を一定の 速さで休まずに走って、40分かかりました。 帰りの自転車の速さは、分速何mですか。
この動画を見る
第58回速さのグラフ ※基本編① ―
例題
次のグラフは、けいこさんが家から駅まで自転車で行ったときのようすを 表したものです。
家からはじめは分速180mで進み、途中、図書館で 15分間調べものをしました。
その後、図書館からは分速200mで向かい、家を出てから50分後に駅に着きました。
(1)家から図書館までは、何mありますか。
(2) 図書館から駅までは、何mありますか。
(3)帰りは、駅から家までは、行きと同じ道を一定の 速さで休まずに走って、40分かかりました。 帰りの自転車の速さは、分速何mですか。
【受験算数】時計算:長針と短針が一直線にいつ並ぶ??

単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ算数・小5下#中学受験教材#いろいろな速さの問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
10時から11時の間で長針と短針が一直線上に並ぶのは何時何分の時でしょう。
この動画を見る
10時から11時の間で長針と短針が一直線上に並ぶのは何時何分の時でしょう。
動体視力とYouTubeのAIを鍛える数学~全国入試問題解法 #Shorts
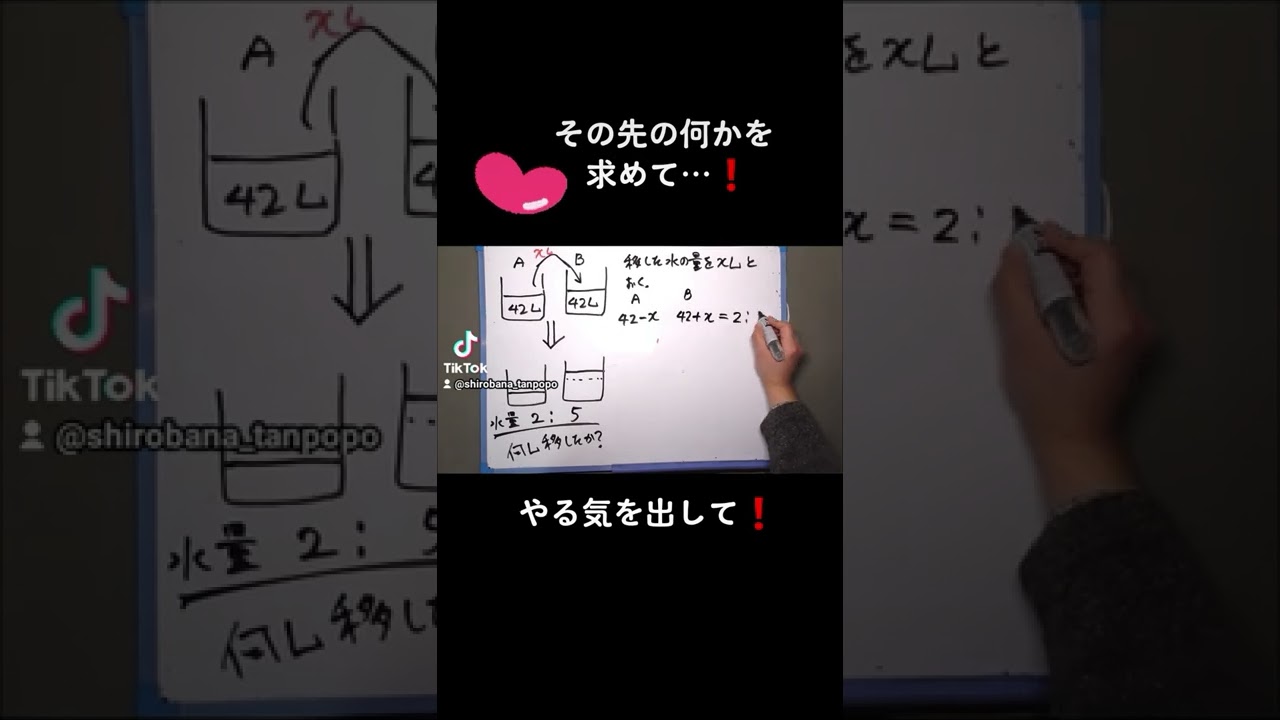
単元:
#数学(中学生)#文章題#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
A,Bともに42L入っている二つの水槽がある.この水量の比が2:5になるようにするには
何Lの水を移せばよいか.
青森県高校過去問
この動画を見る
A,Bともに42L入っている二つの水槽がある.この水量の比が2:5になるようにするには
何Lの水を移せばよいか.
青森県高校過去問
