 数学
数学
 数学
数学
福田の数学〜明治大学2021年理工学部第3問〜単位ベクトルと関数の増減

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
福田の数学〜明治大学2021年理工学部第2問〜格子点と確率

単元:
#数A#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#大学入試解答速報#数学#明治大学#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。$|x|+|y|=2n$を満たす格子点(x,\ y)全体の集合を$D_{2n}$とする。
(1)$D_4$は$\boxed{\ \ あ\ \ }$個の点からなる。一般に、$D_{2n}$は$\boxed{\ \ い\ \ }$個の点からなる。
(2)$D_{2n}$に属する点$(x,\ y)$で$|x-2n|+|y|=2n$を満たすものは全部で$\boxed{\ \ う\ \ }$個ある。
(3)$D_{2n}$に属する点$(x,\ y)$で$|x-n|+|y-n|=2n$を満たすものは全部で$\boxed{\ \ え\ \ }$個ある。
(4)$D_{2n}$から異なる2点$(x_1,\ y_1),\ (x_2,\ y_2)$を無作為に選ぶとき、
$|x_1-x_2|+|y_1-y_2|=2n$
が成り立つ確率は$\boxed{\ \ お\ \ }$である。
2021明治大学理工学部過去問
福田の数学〜明治大学2021年理工学部第1問(4)〜定積分で表された関数と変曲点

単元:
#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(4)連続関数$f(x)$は区間$x \geqq 0$で正の値をとり、区間$x \gt 0$で微分可能
かつ$f'(x)\neq 0$であるとする。さらに、実数の定数aと関数$f(x)$が
$\int_0^x3t^2f(t)dt-(x^3+3)f(x)+\log f(x)=a (x \geqq 0)$
を満たすとする。このとき
$a=-\boxed{\ \ ヌ\ \ }-\log\boxed{\ \ ネ\ \ }$
である。また、曲線$y=f(x)\ (x \gt 0)$の変曲点のx座標をpとすると
$p^3=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。ただし、$\log x$は$x$の自然対数である。
この動画を見る
${\Large\boxed{1}}$(4)連続関数$f(x)$は区間$x \geqq 0$で正の値をとり、区間$x \gt 0$で微分可能
かつ$f'(x)\neq 0$であるとする。さらに、実数の定数aと関数$f(x)$が
$\int_0^x3t^2f(t)dt-(x^3+3)f(x)+\log f(x)=a (x \geqq 0)$
を満たすとする。このとき
$a=-\boxed{\ \ ヌ\ \ }-\log\boxed{\ \ ネ\ \ }$
である。また、曲線$y=f(x)\ (x \gt 0)$の変曲点のx座標をpとすると
$p^3=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$である。ただし、$\log x$は$x$の自然対数である。
福田の数学〜明治大学2021年理工学部第1問(3)〜複素数平面と図形

単元:
#数A#図形の性質#複素数平面#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)複素数$z$と正の実数rは、等式
$z^4=r(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi) \ldots(*)$
を満たしている。ただし、$i$は虚数単位である。
$(\textrm{i})z$の偏角$\thetaを0 \leqq \theta \lt 2\pi$の範囲にとるとき、$\theta$のとりうる値の
うち最小のものは$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}\pi$であり、最大のものは$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\pi$である。
$(\textrm{ii})$等式(*)と等式
$|z-i|=1$
が共に成り立つとき、$r$の値は$r=\boxed{\ \ ナ\ \ }$または$r=\boxed{\ \ ニ\ \ }$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(3)複素数$z$と正の実数rは、等式
$z^4=r(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi) \ldots(*)$
を満たしている。ただし、$i$は虚数単位である。
$(\textrm{i})z$の偏角$\thetaを0 \leqq \theta \lt 2\pi$の範囲にとるとき、$\theta$のとりうる値の
うち最小のものは$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}\pi$であり、最大のものは$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\pi$である。
$(\textrm{ii})$等式(*)と等式
$|z-i|=1$
が共に成り立つとき、$r$の値は$r=\boxed{\ \ ナ\ \ }$または$r=\boxed{\ \ ニ\ \ }$である。
2021明治大学理工学部過去問
福田の数学〜明治大学2021年理工学部第1問(2)〜三角関数の最大最小

単元:
#数Ⅱ#三角関数#三角関数とグラフ#加法定理とその応用#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(2)座標平面上に2点$A(\frac{5}{8},0),\ B(0,\frac{3}{2})$をとる。Lは原点を通る直線で、Lが
x軸の正の方向となす角$\thetaは0 \leqq \theta \leqq \frac{\pi}{2}$の範囲にあるとする。ただし、角$\theta$の
符号は時計の針の回転と逆の向きを正の方向とする。点Aと直線Lとの距離を
$d_A$、点Bと直線Lの距離を$d_B$とおく。このとき、
$d_A+d_B=\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}\sin\theta+\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\cos\theta$
である。$\theta$が$0 \leqq \theta \leqq \frac{\pi}{2}$の範囲を動くとき、
$d_A+d_B$の最大値は$\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}$であり、
最小値は$\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}$である。
2021明治大学理工学部過去問
福田の数学〜明治大学2021年理工学部第1問(1)〜2次方程式が整数を解にもつ条件

単元:
#数Ⅰ#数A#数Ⅱ#2次関数#複素数と方程式#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
【一歩先行く3分間!】二次方程式:東大寺学園高等学校~全国入試問題解法

単元:
#数学(中学生)#2次方程式#高校入試過去問(数学)#数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
この動画を見る
入試問題 東大寺学園高等学校
aの値とpの値を求めよ。
【$x$の二次方程式】
$\sqrt{ 5x^2 }+ax+4\sqrt{ 5 }=0$
の解の1つが
$\sqrt{ 15x }+ax+2\sqrt{ 3 }=0$
の解である。
もう一つの解を pとする。
福田の数学〜明治大学2021年全学部統一入試Ⅲ第4問〜極方程式と曲線で囲まれた面積

単元:
#平面上の曲線#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#媒介変数表示と極座標#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$座標平面の原点Oを極、x軸の正の部分を始線とする極座標$(r,\ \theta)$を考える。
$k \gt 0$として、極方程式
$r(\sqrt{\cos\theta}+\sqrt{\sin\theta})^2=k (0 \leqq \theta \leqq \frac{\pi}{2})$
で表される曲線を$C(k)$とする。曲線$C(k)$上の点を直交座標$(x,\ y)$で表せばxの
とりうる値の範囲は、$\boxed{\ \ ア\ \ } \leqq x \leqq \boxed{\ \ イ\ \ }$である。
曲線$C(k)$とx軸、y軸で囲まれた図形の面積を$S(k)$とおけば、$S(k)=\boxed{\ \ ウ\ \ }$
でなる。直交座標が$(\frac{k}{4},\ \frac{k}{4})$である曲線$C(k)$上の点Aにおける曲線$C(k)$の接線l
の方程式は、$y=\boxed{\ \ エ\ \ }$となる。曲線$C(k)$と直線l、およびx軸で囲まれた
図形の面積を$T(k)$とおけば、$S(k)=\boxed{\ \ オ\ \ }\ T(k)$が成り立つ。$0 \lt m \lt n$を
満たす実数$m,n$に対して、$S(n)-S(m)$が$T(n)$と等しくなるのは、
$\frac{m^2}{n^2}=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ \ \ }}$のときである。
$\boxed{\ \ イ\ \ }\ 、\boxed{\ \ ウ\ \ }$の解答群
$⓪\sqrt k ①k ②k^2 ③\frac{\sqrt 2}{2} ④\frac{\sqrt 2}{3}$
$⑤\frac{k}{2} ⑥\frac{k}{3} ⑦\frac{k^2}{4} ⑧\frac{k^2}{5} ⑨\frac{k^2}{6}$
$\boxed{\ \ エ\ \ }$の解答群
$⓪x+\frac{k}{2} ①x+\frac{k}{4} ②-x+\frac{k}{2} ③-x+\frac{k}{4} ④2x-\frac{k}{2}$
$⑤2x-\frac{k}{4} ⑥2x-\frac{3k}{4} ⑦-2x+\frac{k}{2} ⑧-2x+\frac{k}{4} ⑨-2x+\frac{3k}{4}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{4}}$座標平面の原点Oを極、x軸の正の部分を始線とする極座標$(r,\ \theta)$を考える。
$k \gt 0$として、極方程式
$r(\sqrt{\cos\theta}+\sqrt{\sin\theta})^2=k (0 \leqq \theta \leqq \frac{\pi}{2})$
で表される曲線を$C(k)$とする。曲線$C(k)$上の点を直交座標$(x,\ y)$で表せばxの
とりうる値の範囲は、$\boxed{\ \ ア\ \ } \leqq x \leqq \boxed{\ \ イ\ \ }$である。
曲線$C(k)$とx軸、y軸で囲まれた図形の面積を$S(k)$とおけば、$S(k)=\boxed{\ \ ウ\ \ }$
でなる。直交座標が$(\frac{k}{4},\ \frac{k}{4})$である曲線$C(k)$上の点Aにおける曲線$C(k)$の接線l
の方程式は、$y=\boxed{\ \ エ\ \ }$となる。曲線$C(k)$と直線l、およびx軸で囲まれた
図形の面積を$T(k)$とおけば、$S(k)=\boxed{\ \ オ\ \ }\ T(k)$が成り立つ。$0 \lt m \lt n$を
満たす実数$m,n$に対して、$S(n)-S(m)$が$T(n)$と等しくなるのは、
$\frac{m^2}{n^2}=\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ \ \ }}$のときである。
$\boxed{\ \ イ\ \ }\ 、\boxed{\ \ ウ\ \ }$の解答群
$⓪\sqrt k ①k ②k^2 ③\frac{\sqrt 2}{2} ④\frac{\sqrt 2}{3}$
$⑤\frac{k}{2} ⑥\frac{k}{3} ⑦\frac{k^2}{4} ⑧\frac{k^2}{5} ⑨\frac{k^2}{6}$
$\boxed{\ \ エ\ \ }$の解答群
$⓪x+\frac{k}{2} ①x+\frac{k}{4} ②-x+\frac{k}{2} ③-x+\frac{k}{4} ④2x-\frac{k}{2}$
$⑤2x-\frac{k}{4} ⑥2x-\frac{3k}{4} ⑦-2x+\frac{k}{2} ⑧-2x+\frac{k}{4} ⑨-2x+\frac{3k}{4}$
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第3問(2)〜面積と回転体の体積

単元:
#微分とその応用#積分とその応用#接線と法線・平均値の定理#面積・体積・長さ・速度#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$(2)曲線$y=\log x$を$C$とする。$t \gt e$として、C上の点$P(t,\ \log t)$におけるCの
接線lとx軸との交点をQ、y軸との交点をRとおく。また、$(0,\ \log t)$で表される
点を$S$とおく。点Qのx座標は$\boxed{\ \ ウ\ \ }$であり、点Rのy座標は$\boxed{\ \ エ\ \ }$である。
座標平面の原点をOとすると、$a \gt 0$のとき、線分ORと線分RSの長さの比が
$a:1$となるのは、$t=\boxed{\ \ オ\ \ }$のときである。したがって、三角形OQRの面積が
三角形SPRの面積の9倍となるのは、$t=\boxed{\ \ カ\ \ }$のときである。
曲線Cとx軸、および直線$x=\boxed{\ \ カ\ \ }$で囲まれた図形をy軸のまわりに一回転
させてできる回転体の体積は$\boxed{\ \ キ\ \ }\pi$となる。
$\boxed{\ \ ウ\ \ }\ 、\boxed{\ \ エ\ \ }$の解答群
$⓪1-\log t ①1-2\log t ②\log t-1 ③2\log t-1 ④t(1-\log t)$
$⑤t(1-\log t) ⑥t(\log t-1) ⑦t(2\log t-1) ⑧2t(1-\log t) ⑨2t(\log t-1)$
$\boxed{\ \ オ\ \ }$の解答群
$⓪1-\log t ①1-2\log t ②\log t-1 ③2\log t-1 ④t(1-\log t)$
$⑤t(1-2\log t) ⑥t(\log t-1) ⑦t(2\log t-1) ⑧2t(1-\log t) ⑨2t(\log t-1)$
$\boxed{\ \ カ\ \ }\ 、\boxed{\ \ キ\ \ }$の解答群
$⓪\ e^4 ①\ e^8 ②\ \frac{e^4-1}{2} ③\ \frac{e^8-1}{2} ④\ \frac{5e^4-1}{2}$
$⑤\ \frac{9e^8-1}{2} ⑥\ \frac{3e^4+1}{2} ⑦\ \frac{7e^8+1}{2} ⑧4e^8-e^4+1 ⑨3e^8+1$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{3}}$(2)曲線$y=\log x$を$C$とする。$t \gt e$として、C上の点$P(t,\ \log t)$におけるCの
接線lとx軸との交点をQ、y軸との交点をRとおく。また、$(0,\ \log t)$で表される
点を$S$とおく。点Qのx座標は$\boxed{\ \ ウ\ \ }$であり、点Rのy座標は$\boxed{\ \ エ\ \ }$である。
座標平面の原点をOとすると、$a \gt 0$のとき、線分ORと線分RSの長さの比が
$a:1$となるのは、$t=\boxed{\ \ オ\ \ }$のときである。したがって、三角形OQRの面積が
三角形SPRの面積の9倍となるのは、$t=\boxed{\ \ カ\ \ }$のときである。
曲線Cとx軸、および直線$x=\boxed{\ \ カ\ \ }$で囲まれた図形をy軸のまわりに一回転
させてできる回転体の体積は$\boxed{\ \ キ\ \ }\pi$となる。
$\boxed{\ \ ウ\ \ }\ 、\boxed{\ \ エ\ \ }$の解答群
$⓪1-\log t ①1-2\log t ②\log t-1 ③2\log t-1 ④t(1-\log t)$
$⑤t(1-\log t) ⑥t(\log t-1) ⑦t(2\log t-1) ⑧2t(1-\log t) ⑨2t(\log t-1)$
$\boxed{\ \ オ\ \ }$の解答群
$⓪1-\log t ①1-2\log t ②\log t-1 ③2\log t-1 ④t(1-\log t)$
$⑤t(1-2\log t) ⑥t(\log t-1) ⑦t(2\log t-1) ⑧2t(1-\log t) ⑨2t(\log t-1)$
$\boxed{\ \ カ\ \ }\ 、\boxed{\ \ キ\ \ }$の解答群
$⓪\ e^4 ①\ e^8 ②\ \frac{e^4-1}{2} ③\ \frac{e^8-1}{2} ④\ \frac{5e^4-1}{2}$
$⑤\ \frac{9e^8-1}{2} ⑥\ \frac{3e^4+1}{2} ⑦\ \frac{7e^8+1}{2} ⑧4e^8-e^4+1 ⑨3e^8+1$
2021明治大学全統過去問
【意外と難しい⁈誰でも納得できる5分間!】図形:中央大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#図形の性質#高校入試過去問(数学)#数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
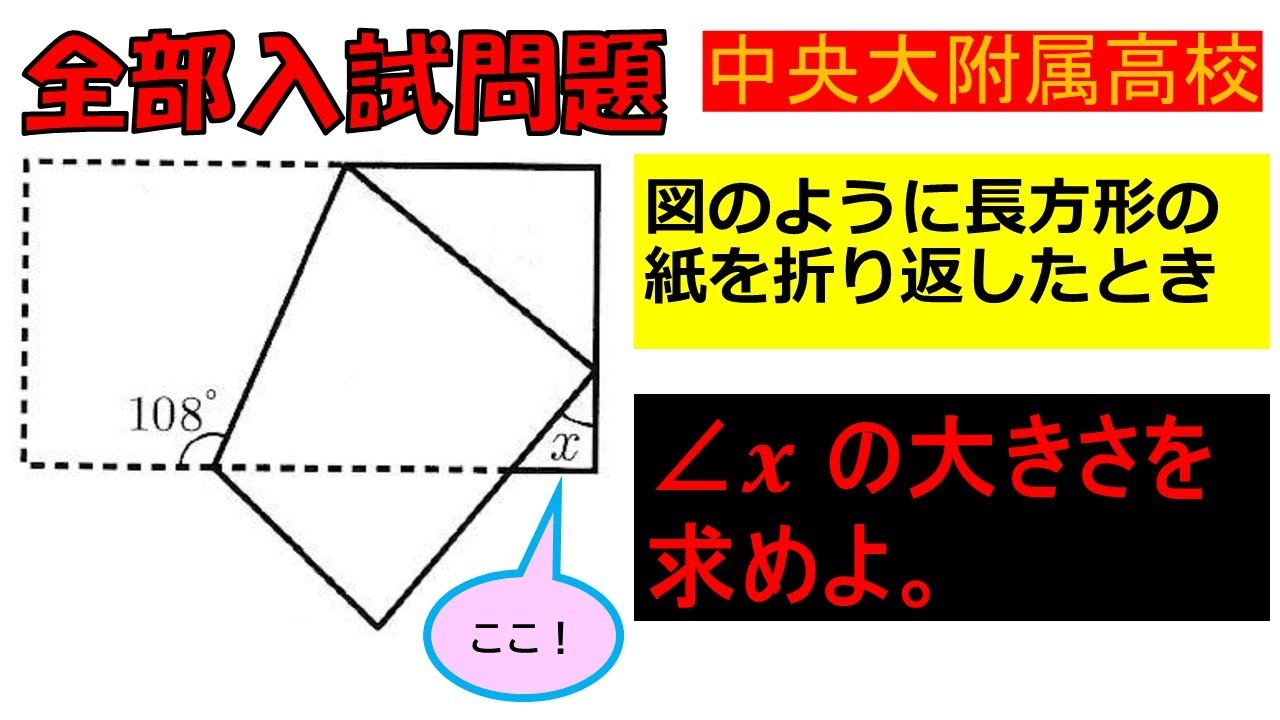
入試問題 中央大学附属高等学校
図のように長方形の 紙を折り返したとき
$\angle x$の大きさを 求めよ。
※図は動画内参照
この動画を見る
入試問題 中央大学附属高等学校
図のように長方形の 紙を折り返したとき
$\angle x$の大きさを 求めよ。
※図は動画内参照
福田の数学〜明治大学2021年全学部統一入試Ⅲ第3問(1)〜定積分と極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(2)〜2次方程式の解が同一円周上にある条件

単元:
#数Ⅱ#2次関数#図形の性質#複素数平面#2次方程式と2次不等式#周角と円に内接する四角形・円と接線・接弦定理#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(1)〜楕円と複素数平面

単元:
#平面上の曲線#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#2次曲線#複素数平面#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第1問〜関数の増減と面積

単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
この動画を見る
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
福田の数学〜明治大学2021年全学部統一入試IⅡAB第3問〜平面幾何とベクトル

単元:
#数A#図形の性質#平面上のベクトル#周角と円に内接する四角形・円と接線・接弦定理#平面上のベクトルと内積#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$辺の長さが2である正六角形ABCDEFがあり、点O,P,Qは次の条件を満たす。
・点Oは辺AB上にある。
・点Pは正六角形ABCDFの内部にある。
・点Qは線分CP上にある。
・三角形OCPと三角形OQFは共に正三角形である。
(1)四角形OQPFに着目すると、$\angle OFQ=\angle OPQ$より、
OQPFは円に内接する四角形なので、$\angle OPF=\boxed{\ \ アイ\ \ }°$とわかる。
(2)$AB //FC$に着目すると、$\triangle OCF=\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}$である。$OC//FP$
であることに着目すると、$\triangle OCP=\triangle OCF$なので、$OC^2=\boxed{\ \ オ\ \ }$とわかる。
また、$OB=\sqrt{\boxed{\ \ カ\ \ }}-\boxed{\ \ キ\ \ }$である。
(3)$OQ^2=OF^2=\boxed{\ \ クケ\ \ }-\boxed{\ \ コ\ \ }\sqrt{\boxed{\ \ サ\ \ }}$であり、
$\overrightarrow{ OQ }=t\ \overrightarrow{ OP }+(1-t)\ \overrightarrow{ OC }$
とおくと、$t$は$t^2-t+\sqrt{\boxed{\ \ シ\ \ }}-\boxed{\ \ ス\ \ }=0$を満たす。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{3}}$辺の長さが2である正六角形ABCDEFがあり、点O,P,Qは次の条件を満たす。
・点Oは辺AB上にある。
・点Pは正六角形ABCDFの内部にある。
・点Qは線分CP上にある。
・三角形OCPと三角形OQFは共に正三角形である。
(1)四角形OQPFに着目すると、$\angle OFQ=\angle OPQ$より、
OQPFは円に内接する四角形なので、$\angle OPF=\boxed{\ \ アイ\ \ }°$とわかる。
(2)$AB //FC$に着目すると、$\triangle OCF=\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}$である。$OC//FP$
であることに着目すると、$\triangle OCP=\triangle OCF$なので、$OC^2=\boxed{\ \ オ\ \ }$とわかる。
また、$OB=\sqrt{\boxed{\ \ カ\ \ }}-\boxed{\ \ キ\ \ }$である。
(3)$OQ^2=OF^2=\boxed{\ \ クケ\ \ }-\boxed{\ \ コ\ \ }\sqrt{\boxed{\ \ サ\ \ }}$であり、
$\overrightarrow{ OQ }=t\ \overrightarrow{ OP }+(1-t)\ \overrightarrow{ OC }$
とおくと、$t$は$t^2-t+\sqrt{\boxed{\ \ シ\ \ }}-\boxed{\ \ ス\ \ }=0$を満たす。
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試IⅡAB第2問〜2つのグラフの共有点の個数と面積

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#微分法と積分法#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
良問を出す大学5選~受けなくても、練習問題に最適な大学はコレだ!【篠原好】

単元:
#センター試験・共通テスト関連#共通テスト#共通テスト(現代文)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大阪大学#防衛大学校#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#大阪大学#共通テスト#共通テスト#共通テスト#共通テスト#共通テスト#共通テスト#北海道大学#青山学院大学#青山学院大学
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
受けなくても、練習問題に最適な大学はコレだ!
「良問を出す大学5選」の紹介です。
この動画を見る
受けなくても、練習問題に最適な大学はコレだ!
「良問を出す大学5選」の紹介です。
【爆速】数学1A解説!!大問4【数学】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
数学1A 大問4解説動画です
この動画を見る
数学1A 大問4解説動画です
【共通テスト】数学1A解説!!大問3【数学】

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
数学1A 大問3解説動画です
この動画を見る
数学1A 大問3解説動画です
【共通テスト】数学1A解説!大問2【数学】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#データの分析#2次関数とグラフ#データの分析#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
数学1A 大問2解説動画です
この動画を見る
数学1A 大問2解説動画です
【共通テスト】爆速!共通テスト数学1Aを解説!!!【数学】

単元:
#大学入試過去問(数学)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
3rd School
問題文全文(内容文):
共通テスト数学1A解説動画です
①
$C:$正の整数
$2x^2+(4C-3)x+2C^2-C-11=0$
②
$C=2$
$2x^2+5x-5=0$
この動画を見る
共通テスト数学1A解説動画です
①
$C:$正の整数
$2x^2+(4C-3)x+2C^2-C-11=0$
②
$C=2$
$2x^2+5x-5=0$
【共通テスト】数学IA_第4問(整数)時間を稼ぐ解答法

単元:
#センター試験・共通テスト関連#共通テスト#数学(高校生)#数学#共通テスト
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共通テスト】数学IA_第4問(整数)解説動画です
この動画を見る
【共通テスト】数学IA_第4問(整数)解説動画です
東大芸人TAWASHIの共通テスト模試結果発表

単元:
#社会(高校生)#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト
指導講師:
Morite2 English Channel
問題文全文(内容文):
東大受験芸人のTAWASHIさんが共通テスト全教科を解いた後に、結果発表をします。
果たして何点取れたのでしょうか!
この動画を見る
東大受験芸人のTAWASHIさんが共通テスト全教科を解いた後に、結果発表をします。
果たして何点取れたのでしょうか!
【東大受験芸人TAWASHI】共通テスト模試全教科耐久ライブ配信

単元:
#数学#共通テスト#英語#化学#物理#共通テスト#共通テスト#共通テスト#世界史#共通テスト
指導講師:
Morite2 English Channel
問題文全文(内容文):
東大受験芸人のTAWASHIさんが共通テスト全教科を解く様子を生配信します。
時間配分を参考にしましょう!
この動画を見る
東大受験芸人のTAWASHIさんが共通テスト全教科を解く様子を生配信します。
時間配分を参考にしましょう!
【共通テスト】数学IA 第1問を瞬時に解くテクニックを解説します(H30試行調査)

