問題文全文(内容文)：
共通テスト英語勉強法解説動画です

問題文全文(内容文)：
共テ70点レベルの英単語テスト
（1）track
（2）sequence
（3）fragile

問題文全文(内容文)：
第1問 次の問い(問1~4)に答えよ。(配点 20)

問1 すべての化学結合が単結合からなる物質として最も適当なものを、次の①~ ④のうちから一つ選べ。 1

①CH3CHO

②C2H2

③ Br2

④BaCl 2

問2 次の文章を読み、下線部(a)・(b)の状態を示す用語の組合せとして最も適当な ものを、後の①~⑧③のうちから一つ選べ。 2

海藻であるテングサを乾燥し、熱湯で溶出させると流動性のあるコロイド溶 液が得られる。この溶液を冷却すると(a)流動性を失ったかたまりになる。さ らに、このかたまりから水分を除去すると(ｂ)乾燥した寒天ができる。
※動画の図参照

問3 水蒸気を含む空気を温度一定のまま圧縮すると、全圧の増加に比例して水蒸 気の分圧は上昇する。水蒸気の分圧が水の飽和蒸気圧に達すると、水蒸気の一 部が液体の水に凝縮し、それ以上圧縮しても水蒸気の分圧は水の飽和蒸気圧と 等しいままである。

分圧$3 .0×10^3$ Pa の水蒸気を含む全圧 $1.0×10^3$Pa ,温度300K,体積 24.9 L の空気を、気体を圧縮する装置を用いて、温度一定のまま、体積8.3Lにまで 圧縮した。この過程で水蒸気の分圧が300Kにおける水の飽和蒸気圧であ $3.6×10^3$Paに達すると、水蒸気の一部が液体の水に凝縮し始めた。図1は 圧縮前と圧縮後の様子を模式的に示したものである。圧縮後に生じた液体の水 の物質量は何molか、最も適当な数値を、後の①~⑥のうちから一つ選べ。 ただし、気体定数は $R = 8.3×10^3$式量 72)の結晶構造に関する次の記述を読み、後の問 い(a~c)に答えよ。

問4 硫化カルシウム CaS (式量 72)の結晶構造に関する次の記述を読み、後の問 い(a~c)に答えよ。

CaSの結晶中では、カルシウムイオン $Ca^2+$ と硫化物イオンSが図2に 示すように規則正しく配列している。結品中の$Ca^-2+$と-の配位数はいずれ もアで、単位格子は$Ca^2+$ と²がそれぞれ4個ずつ含まれる立方体で ある。隣り合う $Ca^2+$ とは接しているが、 (a) 電荷が等しい $Ca^2+$ どうし。 およびぶどうしは、結晶中で互いに接していない。$Ca^2+$のイオン半径をca.$ S^2$のイオン半径をR』とすると$rca < Rs$であり、CaSの結品の単位格 子の体積はイ で表される。

a 空欄 ア・イ に当てはまる数字または式として最も適当なもの を、それぞれの解答群の①~⑤のうちから一つずつ選べ。

アの解答群

①4

➁6

③8

④10

⑤12

イの解答群　5

① $V=８(Rs^3 +rca)^3$

➁$V = 32(Rs^3 + rcs^3)$

③$V =(Rs+rca )^3$

④$V = \dfrac{16}{3}\pi (Rs^3 + rcs^3)$

⑤$V = \dfrac{4}{3}\pi(Rs^3+ rcs^3)$

b エタノール 40mLを入れたメスシリンダーを用意し、CaSの結品40gを このエタノール中に加えたところ、結晶はもとの形のまま溶けずに沈み、 図3に示すように、40の日盛りの位置にあった液面が55の日盛りの位置に 移動した。この結晶の単位格子の体積は何cm²か。最も適当な数値を、 後の①~⑤のうちから一つ選べ。ただし、アボガドロ定数を $6 .0×1０^{23} / mol$ とする。 6 cm ³

①$4.5×10^{-23}$

➁$1.8×10^{-23}$

③$3.6×10^{-22}$

④$6.6×10^{-22}$

⑤$1.3×10^{-21}$

c 図2に示すような配列の結晶構造をとる物質はCaS以外にも存在する。 そのような物質では、下線部(a)に示すのと同様に、結晶中で陽イオンどう し、および陰イオンどうしが互いに接していないものが多い。結品を構成す る2種類のイオンのうち、イオンの大きさが大きい方のイオン半径をR.小 さい方のイオン半径をとして結晶の安定性を考える。このとき、Rが エ 「以上になると、図2に示す単位格子の断面の対角 線(破線)上で大きい方のイオンどうしが接するようになる。その結果、この 結晶構造が不安定になり、異なる結晶構造をとりやすくなることが知られて いる。 +

空欄 ウ エ に当てはまる数字として最も適当なものを、後の ①~⑩のうちから一つずつ選べ。ただし、同じものを繰り返し選んでもよ い。

問題文全文(内容文)：
第1問 次の問い(問1~5)に答えよ。(配点 20)

問1 原子がL殻に電子を3個もつ元素を、次の①~⑤のうちから一つ選べ。1

① Al

➁B

③ LI

④Mg

⑤N

問2 表1に示した窒素化合物は肥料として用いられている。これらの化合物のう ち、窒素の含有率(質量パーセント)が最も高いものを、後の①~④のうちから 一つ選べ。 2

①$NH_4 CI$

➁$(NH_2)_2 CO$

③$NH_4 NO_3$

④$(NH_4）_2 SO_4$

問3 2種類の貴ガス(希ガス)AとBをさまざまな割合で混合し、温度一定のも とで体積を変化させて、全圧が一定値か。になるようにする。元素Aの原子量 が元素Bの原子量より小さいとき、貴ガスの分圧と混合気体の密度の関係 を表すグラフはどれか。最も適当なものを、次の①~⑤のうちから一つ選べ。

3

問4 非品質に関する記述として誤りを含むものはどれか。最も適当なものを、次 の①~④のうちから一つ選べ。 4

① ガラスは一定の融点を示さない。

② アモルファス金属やアモルファス合金は、高温で融解させた金属を急速に 冷却してつくられる。

③ 非品質の二酸化ケイ素は、光ファイバーに利用される。

④ ポリエチレンは、非晶質の部分(非結晶部分・無定形部分)の割合が増える ほどかたくなる。

問5 空気の水への溶解は、水中生物の呼吸(酸素の溶解)やダイバーの減圧症(溶 解した窒素の遊離)などを理解するうえで重要である$1.0×10^5 Pa$の$N_2$と$O_2$の 溶解度(水1Lに溶ける気体の物質量)の温度変化をそれぞれ図1に示す。$N_2$と$O_2$ の水への溶解に関する後の問い (a・b) に答えよ。ただし、$N_2$ と$O_2$ の水への溶解は、ヘンリーの法則に従うものとする。

a $1.0×10^5 Pa$で$○_2$が水20Lに接している。同じ圧力で温度を 10℃ から 20℃にすると、水に溶解している $O_2$の物質量はどのように変化するか。 最も適当な記述を、次の①~⑤のうちから選べ。 5

①$3.5×10^{-4}$mol 減少する。

➁$7.0×10^{-3}$mol 減少する。

③ 変化しない。

④$3.5×10^{-4}$mol 増加する。

⑤ $7.0×10^{-3}$mol 増加する。

問題文全文(内容文)：
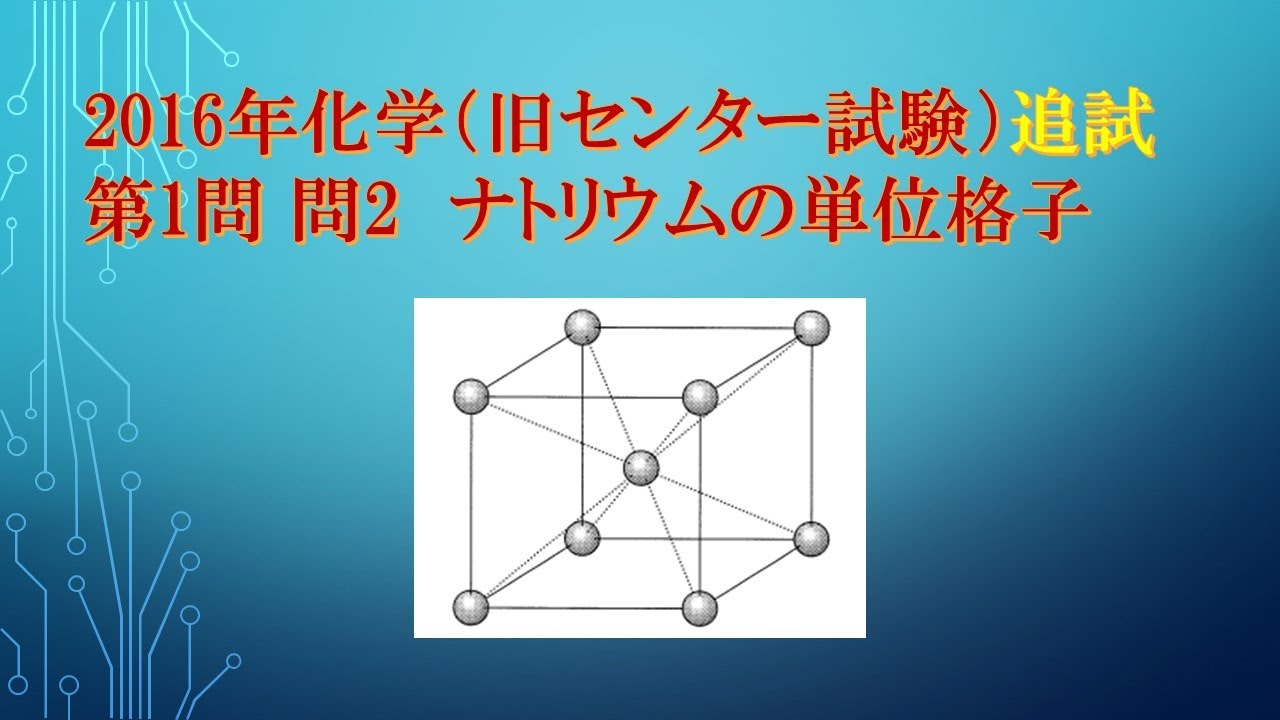
金属結晶では、金属原子が規則正しく配列している。
金属ナトリウムの単位格子は、図1の立方体で表される。
金属ナトリウムの密度を$d[g/cm^3]$.
ナトリウムのモル質量を$W(g/mol]$、
アボガドロ定数を$N_{A} 〔/mol〕$としたとき、
単位格子の体積を表す式として正しいものを、
下の①～⑥のうちから一つ選べ。

①$\displaystyle \frac{WN_{A}}{d}$
②$\displaystyle \frac{2WN_{A}}{d}$
③$\displaystyle \frac{5WN_{A}}{d}$
④$\displaystyle \frac{W}{dN_{A}}$
⑤$\displaystyle \frac{2W}{dN_{A}}$
⑥$\displaystyle \frac{5W}{dN_{A}}$

問題文全文(内容文)：
共有結合を含まない物質を、次の①～⑥のうちから一つ選べ。

①水素　②オゾン　③カリウム　
④単斜硫黄　⑤ベンゼン　⑥塩化水素　

問題文全文(内容文)：
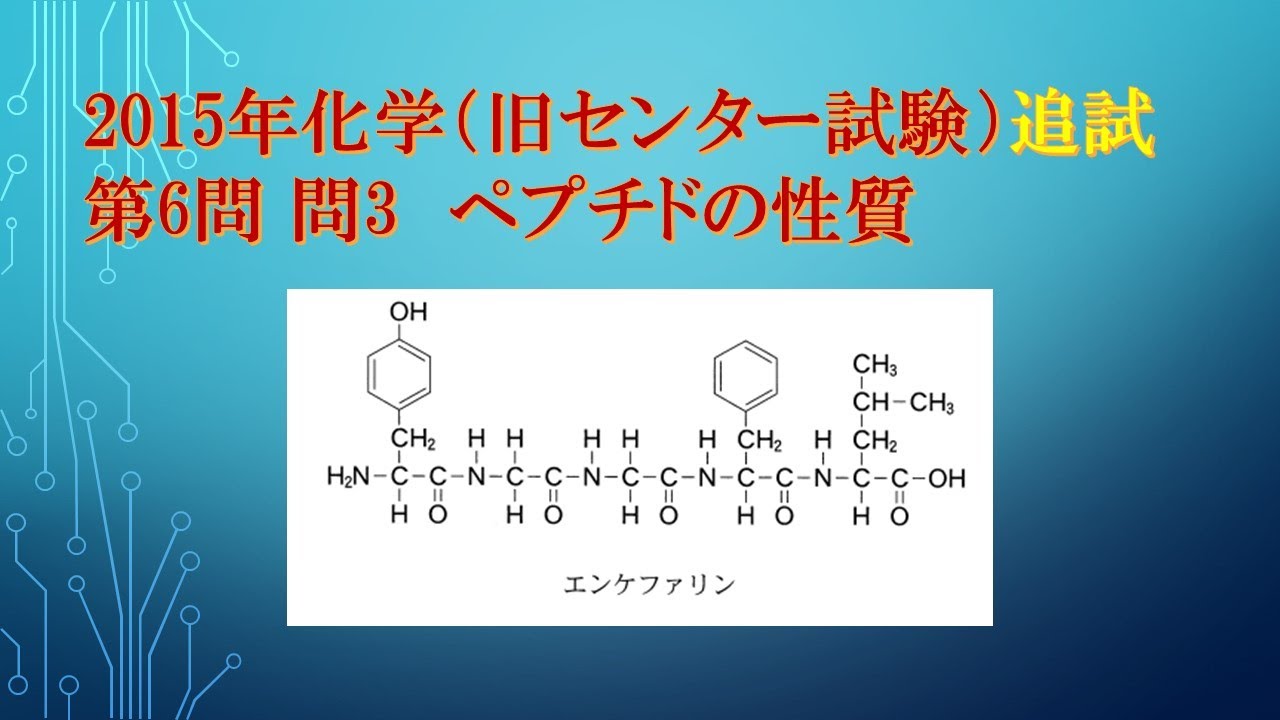
次の構造式で示される化合物エンケファリンは、脳内鎮痛ペプチドである。
この化合物に対して実験Ⅰおよび実験Ⅱを行った。
これらの実験の結果として 最も適当なものを、下の①～⑤のうちから一つずつ選べ。
ただし、同じものを 選んでもよい。

実験Ⅰ:水酸化ナトリウム水溶液と少量の薄い硫酸銅(Ⅱ) 水溶液を加えた。
実験Ⅰの結果 $\boxed{ 3 }$

実験Ⅱ:濃硝酸を加えて加熱した。
実験Ⅱの結果 $\boxed{ 4 }$

① 赤紫色になった。
② 黄色になった。
③ 黒色沈殿を生じた。
④ 白色沈殿を生じた。
⑤ 色の変化はなく、沈殿も生じなかった。

※図は動画内参照

問題文全文(内容文)：
天然に存在する核酸に関する記述として誤りを含むものを、次の①～⑤のう ちから一つ選べ。

① 核酸の単量体に相当する分子をヌクレオチドという。
② 核酸は、それを構成する糖のヒドロキシ基とリン酸が縮合した構造をもつ。
③ $RNA$は5種類の塩基をもつ。
④ $DNA$は4種類の塩基をもつ。
⑤ $DNA$ の二重らせん構造では、塩基どうしが水素結合を形成している。

問題文全文(内容文)：
グルコースとセルロースに関する記述として誤りを含むものを、次の①～⑤ のうちから一つ選べ。

① グルコースは、5個のヒドロキシ基をもつ。
② 結晶状態のグルコースは、六員環の構造をもつ。
③ グルコースは、フルクトースの構造異性体である。
④ セルロース中にあるグルコース単位には、4個のヒドロキシ基が存在する。
⑤ セルロースは、デンプンのようならせん状ではなく、直線状の構造をとる。

問題文全文(内容文)：
アジビン酸(分子量$146$)を濃硫酸を触媒として十分な量のメタノールと反応させ、完全にエステル化した。
このとき分子内に二つのエステル結合をもつ 化合物が$3.48g$生成した。
この反応で生成した水の質量は何$g$か。
最も適当な数値を、下の①～⑤のうちから一つ選べ。
アジビン酸：$HOOC-(CH_2)_4-COOH$
原子量：$H1 C12 O16$

①$0.36$ ②$0.39$ ③$0.60$
④$0.72$ ⑤$0.78$

問題文全文(内容文)：
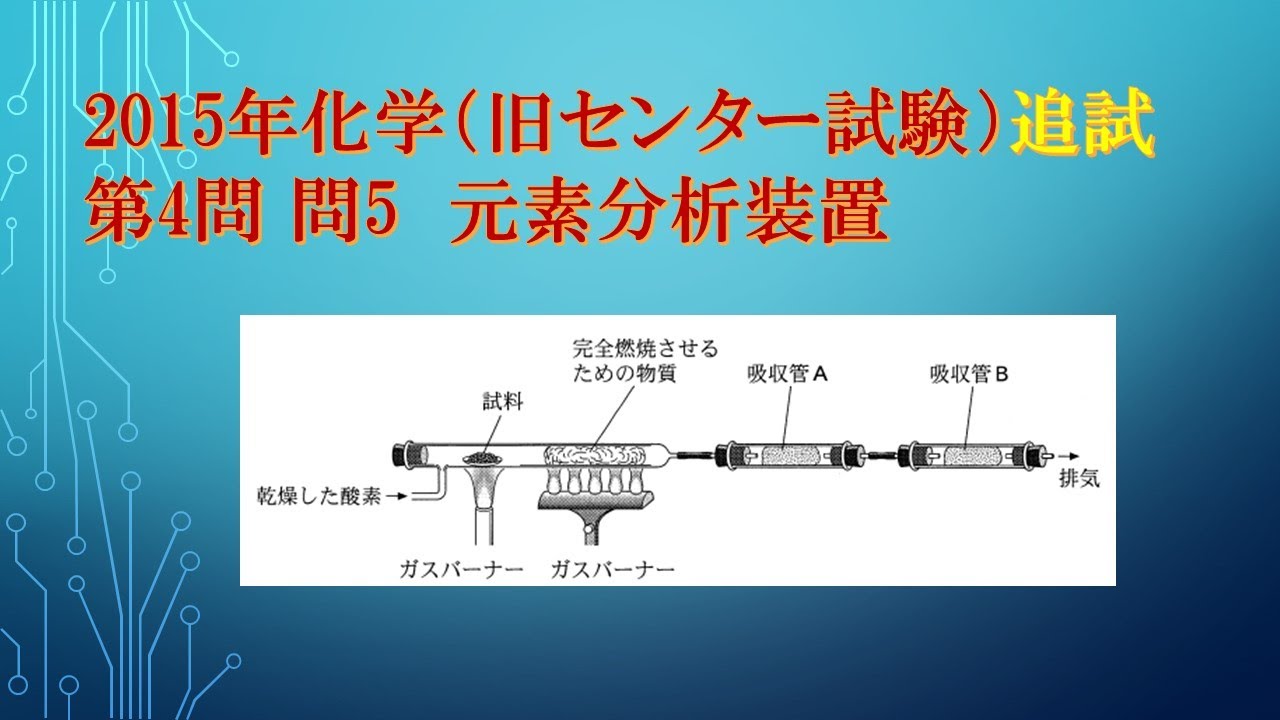
図1は、炭素、水素、酸素からなる有機化合物の元素分析を行うための装置を示している。
試料を完全燃焼させ、発生する2種類の気体を吸収管$A$と吸 収管$B$でそれぞれ吸収させる。
吸収管$A$に入れる物質と吸収管$B$で吸収させる物質の組合せとして最も適当なものを、下の①～⑥のうちから一つ選べ。
※図は動画内参照

問題文全文(内容文)：
共通テスト　80点レベルの英単語クイズ

問題文全文(内容文)：
物理・化学の質問に答える動画です

問題文全文(内容文)：
指数・対数の解説動画です

問題文全文(内容文)：
物理・化学の質問に答える動画です

問題文全文(内容文)：
物理・化学の質問に答える動画です

問題文全文(内容文)：
共通テスト数学のコツ（伸ばしやすい単元）紹介動画です

問題文全文(内容文)：
共通テスト英語のコツ3選紹介動画です

問題文全文(内容文)：
純水1kgに溶質$0.1mol/L$を溶かした水溶液を冷却したとき、
凝固点降下が最も大きくなる溶質を、次の①～⑤のうちから一つ選べ。
ただし、電解質の電離 度は1とする。

① 酢酸ナトリウム
③ 塩化マグネシウム
② 塩化カリウム
④ グリセリン
⑤ グルコース

問題文全文(内容文)：
固体の構造や結合に関する記述として下線部に誤りを含むものを、次の①～⑤のうちから一つ選べ。

① 体心立方格子をもつ金属の結晶構造は、最密構造である。
② 塩化ナトリウムは、陽イオンと陰イオンとの間の静電気的な引力によりイオン結晶をつくる。
③ ケイ素の結晶は、共有結合からなる。
④ ドライアイスは、分子どうしが弱い分子間力により規則正しく配列してい る結晶である。
⑤ ガラスは、非品質である。

問題文全文(内容文)：
$20℃,1.013×10^5 Pa$で$560mL$の塩化水素を純水に溶かし、塩酸$50mL$をつくった。
この塩酸のモル濃度は何$mol/L$か。
最も適当な数値を、次の①～⑥のうちから一つ選べ。

① $0.025$
② $0.050$
③ $0.25$
④ $0.50$
⑤ $2.5$
⑥ $5.0$

問題文全文(内容文)：
英語の速読　意識すべき4つのポイント紹介動画です

問題文全文(内容文)：
周期表中の水素以外の典型元素の記述として適当なものを、
次の①～⑤のうちから選べ。

① 同族元素の原子は、同数の価電子をもつ。
② 同族元素の原子は、同じ電子配置をもつ。
③ 同族元素では、化学的性質が互いに類似している。
④ 同一周期では、右にある原子ほど陽子の数が多くなる。
⑤ 第3周期の原子では、最外殻電子がM殻にある。

問題文全文(内容文)：
4 下線部(d)に関する次の問い(a・b)に答えよ。

a 浸透圧 Π に関するファントホッフの法則は,次の式(Ⅰ)のように表すことができる。

$Π = \displaystyle \frac{C_wRT}{M} $

ここで,$C_w$ は質量濃度とよばれ,溶質の質量$w$,溶液の体積 $V$ を用いて
$C_w = \displaystyle \frac{w}{V}$で定義される。
また,$R$ は気体定数,$T$ は絶対温度,$M$ は溶質のモル質量である。
式(1)はスクロースなどの比較的低分子量の非電解質の$M$
の決定に広く用いられている。
$300K,C_w =0.342g/L$のスクロース(分子量 $342$)水溶液の$Π$ は何 $Pa$か。
その数値を有効数字桁の次の形式で表すとき, $\boxed{ 28 } ～\boxed{ 30 } $ に当てはまる数字を,後の①～⓪のうちから一つずつ選べ。
ただし,同じものを繰り返し選んでもよい。
なお,気体定数は $R =8.31×10^3 Pa・L/(K・mol)$とする。
①$1$ ②$2$ ③$3$ ④$4$ ⑤$5$
⑥$6$ ⑦$7$ ⑧$8$ ⑨$9$ ⓪$0$

問題文全文(内容文)：
下線部(d)に関する次の問い(a・b)に答えよ。

a 浸透圧 $Π$ に関するファントホッフの法則は,
次の式(Ⅰ)のように表すことができる。
$Π =\displaystyle \frac{ C_w RT}{M}$
ここで,$C_w$は質量濃度とよばれ,溶質の質量$w$溶液の体積 $V$ を用いて
$C_w = \displaystyle \frac{ w}{v}$で定義される。
また,$R$ は気体定数,$T$ は絶対温度,$M$ は溶質のモル質量である。
式(Ⅰ)はスクロースなどの比較的低分子量の非電解質の$M$
の決定に広く用いられている。
$300K,C_w =0.342g/L$のスクロース(分子量 342)
水溶液の$Π$ は何$Pa$か。
その数値を有効数字桁の次の形式で表すとき, $\boxed{ 28 } ～\boxed{ 30 }$ に
当てはまる数字を,後の①～⓪のうちから一つずつ選べ。
ただし,同じものを繰り返し選んでもよい。
なお,気体定数は $R =8.31×10^3 Pa・L/(K・mol)$とする。

①$1$ ②$2$ ③$3$ ④$4$ ⑤$5$
⑥$6$ ⑦$7$ ⑧$8$ ⑨$9$ ⓪$0$

問題文全文(内容文)：
図1に示す塩化カリウム$KCI$. 硝酸カリウム$KNO_3$, および硫酸マグネシウ$MgSO_4$の水に対する溶解度曲線を用いて、
固体の溶解および析出に関する後の問い(a・b)に答えよ。

b $MgSO_4$の水溶液を冷却して得られる結晶は、$MgSO_4$の水和物である。
水$100g$に、ある量の$MgSO_4$が溶けている水溶液Aを$14℃$に冷却する。
このとき、析出する$MgSO_4$の水和物の質量が$12.3g$であり、その中の水和水の質量が$6.3g$である場合、冷却前の水溶液Aに溶けている$MgSO_4$の質量は何$g$か。
最も適当な数値を、次の①～⑥のうちから一つ選べ。

①$28$ ②$30$ ③$32$ ④$34$ ⑤$36$ ⑥$42$
※図は動画内参照

問題文全文(内容文)：
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$,　σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400,　標本平均が30.0g,　標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針：Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }},　\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ　①$\sigma^2$　②$\frac{\sigma}{\sqrt n}$　③$\frac{\sigma^2}{n}$
④m　⑤2m　⑥$m^2$　⑦$\sqrt m$　
⑧$\frac{\sigma}{n}$　⑨$n\sigma　$ⓐ$nm$　ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪～⑤のうちから一つ選べ。
⓪28.6≦m≦31.4　①28.7≦m≦31.3　②28.9≦m≦31.1　
③29.6≦m≦30.4　④29.7≦m≦30.3　⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法：無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2　...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$～$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k　①2k　②3k　③$\frac{50+k}{2}$
④$\frac{25+k}{2}$　⑤25+k　⑥$\frac{\sqrt{50+k}}{2}$　⑦$\frac{50+k}{4}$

2023共通テスト過去問

問題文全文(内容文)：
第5問
三角錐PABCにおいて、辺BCの中点をMとおく。また、$\angle$PAB=$\angle$PACとし、この角度をθをおく。0°＜ θ ＜ 90°とする。
(1)$\overrightarrow{AM}$は
$\overrightarrow{AM}$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\overrightarrow{AB}$+$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}\overrightarrow{AC}$
と表せる。また
$\frac{\overrightarrow{AP}・\overrightarrow{AB}}{|\overrightarrow{AP}||\overrightarrow{AB}|}$=$\frac{\overrightarrow{AP}・\overrightarrow{AC}}{|\overrightarrow{AP}||\overrightarrow{AC}|}$=$\boxed{\boxed{\ \ オ\ \ }}$　　...①
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$\sin \theta$　①$\cos \theta$　②$\tan \theta$　
③$\frac{1}{\sin \theta}$　④$\frac{1}{\cos \theta}$　⑤$\frac{1}{\tan \theta}$　
⑥$\sin\angle$BPC　⑦$\cos\angle$BPC　⑧$\tan\angle$BPC
(2)θ=45°とし、さらに
$|\overrightarrow{AP}|$=3√2,　$|\overrightarrow{AB}|$=$|\overrightarrow{PB}|$=3,　$|\overrightarrow{AC}|$=$|\overrightarrow{PC}|$=3
が成り立つ場合を考える。このとき
$\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$=$\boxed{\ \ カ\ \ }$
である。さらに、直線AM上の点Dが$\angle$APD=90°を満たしているとする。このとき、$\overrightarrow{AD}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$である。
(3)
$\overrightarrow{AQ}$=$\boxed{\ \ キ\ \ }\overrightarrow{AM}$
で定まる点をQとおく。$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直である三角錐PABCはどのようなものかについて考えよう。例えば(2)の場合では、点Qは点Dと一致し、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
(i)$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であるとき、$\overrightarrow{PQ}$を$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AP}$を用いて表して考えると、$\boxed{\boxed{\ \ ク\ \ }}$が成り立つ。さらに①に注意すると、$\boxed{\boxed{\ \ ク\ \ }}$から$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つことがわかる。
したがって、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であれば、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立つ。逆に、$\boxed{\boxed{\ \ ケ\ \ }}$が成り立てば、$\overrightarrow{PA}$と$\overrightarrow{PQ}$は垂直である。
$\boxed{\boxed{\ \ ク\ \ }}$の解答群
⓪$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AP}・\overrightarrow{AP}$
①$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AP}・\overrightarrow{AP}$
②$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$\overrightarrow{AB}・\overrightarrow{AC}$
③$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=$-\overrightarrow{AB}・\overrightarrow{AC}$
④$\overrightarrow{AP}・\overrightarrow{AB}$+$\overrightarrow{AP}・\overrightarrow{AC}$=0
⑤$\overrightarrow{AP}・\overrightarrow{AB}$-$\overrightarrow{AP}・\overrightarrow{AC}$=0
$\boxed{\boxed{\ \ ケ\ \ }}$の解答群
⓪$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$\sqrt 2|\overrightarrow{BC}|$
①$|\overrightarrow{AB}|$+$|\overrightarrow{AC}|$=$2|\overrightarrow{BC}|$
②$|\overrightarrow{AB}|\sin\theta$+$|\overrightarrow{AC}|\sin\theta$=$|\overrightarrow{AP}|$
③$|\overrightarrow{AB}|\cos\theta$+$|\overrightarrow{AC}|\cos\theta$=$|\overrightarrow{AP}|$
④$|\overrightarrow{AB}|\sin\theta$=$|\overrightarrow{AC}|\sin\theta$=$2|\overrightarrow{AP}|$
⑤$|\overrightarrow{AB}|\cos\theta$=$|\overrightarrow{AC}|\cos\theta$=$2|\overrightarrow{AP}|$
(ii)kを正の実数とし
$k\overrightarrow{AP}・\overrightarrow{AB}$=$\overrightarrow{AP}・\overrightarrow{AC}$
が成り立つとする。このとき、$\boxed{\boxed{\ \ コ\ \ }}$が成り立つ。
また、点Bから直線APに下ろした垂線と直線APとの交点をB'とし、同様に点Cから直線APに下ろした垂線と直線APとの交点をC'とする。
このとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ サ\ \ }}$であることと同値である。特にk=1のとき、$\overrightarrow{PA}$と$\overrightarrow{PQ}$が垂直であることは、$\boxed{\boxed{\ \ シ\ \ }}$であることと同値である。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$k|\overrightarrow{AB}|$=$|\overrightarrow{AC}|$　①$|\overrightarrow{AB}|$=$k|\overrightarrow{AC}|$　
②$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AB}|$　③$k|\overrightarrow{AP}|$=$\sqrt 2|\overrightarrow{AC}|$
$\boxed{\boxed{\ \ サ\ \ }}$の解答群
⓪B'とC'がともに線分APの中点
①B'とC'が線分APをそれぞれ(k+1):1と1:(k+1)に内分する点
②B'とC'が線分APをそれぞれ1:(k+1)と(k+1):1に内分する点
③B'とC'が線分APをそれぞれk:1と1:kに内分する点
④B'とC'が線分APをそれぞれ1:kとk:1に内分する点
⑤B'とC'がともに線分APをk:1に内分する点
⑥B'とC'がともに線分APを1:kに内分する点
$\boxed{\boxed{\ \ シ\ \ }}$の解答群
⓪$\triangle$PABと$\triangle$PACがともに正三角形
①$\triangle$PABと$\triangle$PACがそれぞれ$\angle$PBA=90°, $\angle$PCA=90°を満たす直角二等辺三角形
②$\triangle$PABと$\triangle$PACがそれぞれBP=BA, CP=CAを満たす二等辺三角形
③$\triangle$PABと$\triangle$PACが合同
④AP=BC

2023共通テスト過去問

問題文全文(内容文)：
第4問
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金を$a_n$万円とおく。ただし、p＞0とし、nは自然数とする。
例えば、$a_1=10+p, a_2=1.01(10+p)+p$である。
(1)$a_n$を求めるために二つの方針で考える。
方針1
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金$a_3$万円について、$a_3=\boxed{\boxed{\ \ ア\ \ }}$である。全ての自然数nについて
$a_{n+1}=\boxed{\boxed{\ \ イ\ \ }}a_n+\boxed{\boxed{\ \ ウ\ \ }}$
が成り立つ。これは
$a_{n+1}+\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}(a_n+\boxed{\boxed{\ \ エ\ \ }})$
と変形でき、$a_n$を求めることができる。

$\boxed{\boxed{\ \ ア\ \ }}$の解答群
⓪1.01{1.01(10+p)+p}　①1.01{1.01(10+p)+1.01p}　
②1.01{1.01(10+p)+p}+p　③1.01{1.01(10+p)+p}+1.01p　
④1.01(10+p)+1.01p　⑤1.01(10+1.01p)+1.01p

$\boxed{\boxed{\ \ イ\ \ }}$～$\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪1.01　①$1.01^{n-1}$　②$1.01^n$　
③p　④100p　⑤np
⑥100np　⑦$1.01^{n-1}$×100p　⑧$1.01^n$×100p　
方針2
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
もともと預金口座にあった10万円は、2年目の初めには10×1.01万円になり、3年目の初めには10×$1.01^2$万円になる。同様に考えるとn年目の初めには10×$1.01^{n-1}$万円になる。
・1年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{カ}}}$万円になる。
・2年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{キ}}}$万円になる。
・n年目の初めに入金したp万円は、n年目の初めにはp万円のままである。
これより
$a_n$=10×$1.01^{n-1}$+p×$1.01^{\boxed{\boxed{カ}}}$+p×$1.01^{\boxed{\boxed{キ}}}$+...+p
=10×$1.01^{n-1}$+p$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$
となることがわかる。ここで、$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$=$\boxed{\boxed{ \ \ ケ\ \ }}$となるので、$a_n$を求めることができる。
$\boxed{\boxed{ \ \ ケ\ \ }}$,　$\boxed{\boxed{ \ \ キ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪n+1　①n　②n-1　③n-2
$\boxed{\boxed{ \ \ ク\ \ }}$の解答群
⓪k+1　①k　②k-1　③k-2
$\boxed{\boxed{ \ \ ケ\ \ }}$の解答群
⓪100×$1.01^n$　①100($1.01^n$-1)　
②100($1.01^{n-1}-1$)　③n+$1.01^{n-1}$-1　
④0.01(101n-1)　⑤$\frac{n×1.01^{n-1}}{2}$
(2)花子さんは、10年目の終わりの預金が30万円以上になるための入金額について考えた。
10年目の終わりの預金が30万円以上であることを不等式を用いて表すと
$\boxed{\boxed{\ \ コ\ \ }}$≧30となる。この不等式をpについて解くと
p≧$\frac{\boxed{\ \ サシ\ \ }-\boxed{\ \ スセ\ \ }×1.01^{10}}{101(1.01^{10}-1)}$
となる。したがって、毎年の初めの入金額が例えば18000円であれば、10年目の終わりの預金が30万円以上になることがわかる。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$a_{10}$　①$a_{10}$+p　②$a_{10}$-p　
③1.01$a_{10}$　④1.01$a_{10}$+p　⑤1.01$a_{10}$-p
(3)1年目の入金を始める前における花子さんの預金が10万円ではなく、13万円の場合を考える。すべての自然数nに対して、この場合のn年目の初めの預金は$a_n$万円よりも$\boxed{\boxed{\ \ ソ\ \ }}$万円多い。なお、年利は1%であり、毎年の初めの入金額はp万円のままである。
$\boxed{\boxed{\ \ ソ\ \ }}$の解答群
⓪3　①13　②3(n-1)　
③3n　④13(n-1)　⑤13n　
⑥$3^n$　⑦3+1.01(n-1)　⑧3×$1.01^{n-1}$　
⑨3×$1.01^n$　ⓐ13×$1.01^{n-1}$　ⓑ13×$1.01^n$　

2023共通テスト過去問

問題文全文(内容文)：
【関関同立当日速報★世界史・日本史】2/2入試　今日を知ることは必ず明日につながります！
代ゼミ世界史＆日本史講師が「今日の入試解析＆大学別狙い＆翌日アドバイス」をしています。