山口大学
山口大学
【高校数学】毎日積分69日目~47都道府県制覇への道~【⑬山口】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
【山口大学 2023】
座標平面上で、不等式
$\displaystyle \frac{1}{4}x^2-2≦y≦0またはx^2+y^2≦4$
の表す領域を$D_1$とし、不等式
$y＞\sqrt{3}xかつx^2+y^2＜2$
の表す領域を$D_2$とし、不等式
$y＞-\sqrt{3}xかつx^2+y^2＜2$
の表す領域を$D_3$とする。また、$D_2$と$D_3$の和集合を$X$とし、$D_1$から$X$を除いた領域を$Y$とする。このとき、次の問いに答えなさい。
(1)領域$D_1$を図示しなさい。
(2)領域$D_1$の面積を求めさない。
(3)領域$Y$を図示しなさい。
(4)領域$Y$の面積を求めなさい。
この動画を見る
【山口大学 2023】
座標平面上で、不等式
$\displaystyle \frac{1}{4}x^2-2≦y≦0またはx^2+y^2≦4$
の表す領域を$D_1$とし、不等式
$y＞\sqrt{3}xかつx^2+y^2＜2$
の表す領域を$D_2$とし、不等式
$y＞-\sqrt{3}xかつx^2+y^2＜2$
の表す領域を$D_3$とする。また、$D_2$と$D_3$の和集合を$X$とし、$D_1$から$X$を除いた領域を$Y$とする。このとき、次の問いに答えなさい。
(1)領域$D_1$を図示しなさい。
(2)領域$D_1$の面積を求めさない。
(3)領域$Y$を図示しなさい。
(4)領域$Y$の面積を求めなさい。
山口大 １の十乗根の問題
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
４次方程式の解と係数の関係 答えがあっていればなんでもいいか！山口大
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
格子点を通るということは？【山口大学】【数学 入試問題】
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
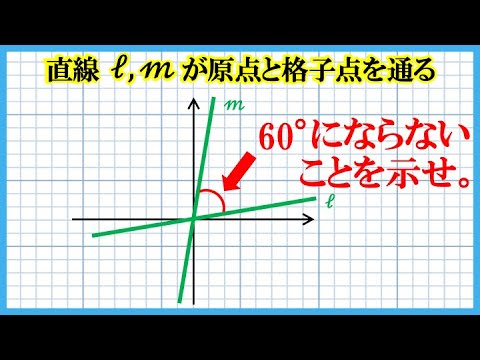
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
この動画を見る
座標平面上で、$x$座標,$y$座標が共に整数である点を格子点という。
原点を通る2直線$l,m$がそれぞれ原点以外にも格子点を通るとき、
$l,m$のなす角は、$60°$にならないことを証明せよ。
ただし、$\sqrt3$が無理数であることを証明なしに用いても良い。
山口大過去問
山口大 ３次方程式の解の個数 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
05年 山口大学
次の方程式 $x^3-kx+2=0$において$k$ が実数であるときの実数解の個数を求めよ。
この動画を見る
05年 山口大学
次の方程式 $x^3-kx+2=0$において$k$ が実数であるときの実数解の個数を求めよ。
山口大（医）場合の数（東大類題）高校数学 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#場合の数と確率#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'03山口大学過去問題
m個の玉(区別無し)を袋A,B,Cに入れる。
A,B,Cに入れる個数をそれぞれx,y,z個
(1)m=18 $x＞y＞z \geqq 0$ 何通りか
(2)m=6n $x＞y＞z \geqq 0$ 何通りか、nで表せ
この動画を見る
'03山口大学過去問題
m個の玉(区別無し)を袋A,B,Cに入れる。
A,B,Cに入れる個数をそれぞれx,y,z個
(1)m=18 $x＞y＞z \geqq 0$ 何通りか
(2)m=6n $x＞y＞z \geqq 0$ 何通りか、nで表せ